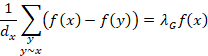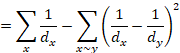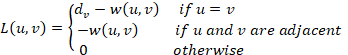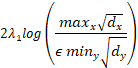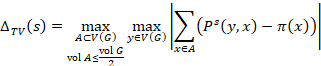《谱图论》读书笔记（第一章）
目录
Chapter 1. 特征值和图的拉普拉斯算子
1.1 介绍
1.2 拉普拉斯算子和特征值
1.3 Basic facts about the spectrum of Graph
1.4 Eigenvalues of weighted graphs
1.5 Eigenvalues and random walks
谱图论作为图卷积神经网络的理论基础。这个暑假利用时间对这部分内容进行了深入学习，由于谱图论只有英文版，由于时间关系进对其部分进行了翻译，随着理解的深入，会陆续对其进行整理和总结，现总结读书笔记如下，
Chapter 1. 特征值和图的拉普拉斯算子
1.1 介绍
谱图理论有着悠久的历史。在早期，矩阵理论和线性代数被用来分析图的矩阵。代数方法在处理规则和对称图时特别有效。有时，某些特征值被称为图的“代数连通性”[126]。谱图理论在代数方面有大量的文献，如Biggs[25]、Cvetkovic、Doob and Sachs[90,91]和Seidel[222]等几项调查和书籍中都有详细的记录。
在过去的十年中，谱图理论的许多发展往往带有几何色彩。例如，由于Lubotzky-Phillips-Sarnak[191]和Margulis[193]的影响，扩展图的显式构造都是基于图的特征值和等周性。Cheeger不等式的离散模拟在随机游动和快速混合马氏链的研究中得到了广泛的应用[222]。新的光谱技术已经出现，它们功能强大，非常适合处理一般图。从某种意义上说，谱图理论已经进入了一个新的时代。
正如天文学家研究恒星光谱以确定遥远恒星的构成一样，图论的主要目标之一就是从图的光谱图(或从一长串易于计算的不变量)中推导出图的主要性质和结构。一般图的谱方法就是朝着这个方向迈出的一步。我们将看到特征值与图的几乎所有主要不变量密切相关，它们将一个极值特性与另一个极值特性联系起来。毫无疑问，特征值在我们对图形的基本理解中起着核心作用。
图特征值的研究实现了与许多数学领域日益丰富的联系。谱图理论和微分几何之间的相互作用是一个特别重要的发展。谱黎曼几何与谱图理论之间有一个有趣的类比。谱几何的概念和方法为研究图的特征值提供了有用的工具和重要的见解，从而导致了谱几何的新方向和结果。代数谱方法也非常有用，特别是对于极值例子和构造。在这本书中，我们采取了一个广泛的方法，强调图形特征值的几何方面，同时也包括代数方面。读者不需要有特殊的几何背景，因为这本书几乎完全是图形理论。
从一开始，光谱图理论就在化学[27]中得到了应用。特征值与分子的稳定性有关。图谱在理论物理和量子力学的各种问题中也很自然地出现，例如在哈密顿系统的能量最小化中。扩展图和特征值的研究是由通信网络中的一些问题引起的。快速混合马尔可夫链的发展与随机逼近算法的进步交织在一起。图形特征值的应用在许多领域以不同的形式出现。然而，谱图理论的基础数学，通过它与纯的和应用的、连续的和离散的所有联系，可以看作是一个统一的学科。这就是我们打算在本书中讨论的方面。
1.2 拉普拉斯算子和特征值
在我们开始定义特征值之前，需要进行一些解释。我们在本书中考虑的特征值与Biggs[25]或Cvetkovic、Doob和Schs中的特征值并不完全相同[90]。基本上，特征值是在这里定义为一般和“标准化”的形式。虽然这看起来有点复杂，但我们的特征值与一般图的其它图不变量有很好地相关，其他定义（例如邻接矩阵的特征值）通常与该定义的特征值一致可能是由于事实它与光谱几何和随机过程中的特征值一致。许多仅为正则图结果可以推广到所有的图。因此，这为一般图提供了统一的处理。关于定义和标准图论术语，读者可以参考[31]。
在图G中，让
表示顶点的度数。我们首先为没有循环的图定义一个多重边的拉普拉斯矩阵(带有循环的一般加权情况将在第1.4节中讨论)。首先，我们考虑矩阵L，定义如下:
设
表示矩阵第项的值为。G的拉普拉斯变换被定义为矩阵：
可以记为：
对于
，约定
。我们说
是一个孤立的顶点。如果一个图至少包含一条边，那么它就被称为非零图（平凡图：仅有一个结点的图的称平凡图；边的集合为空的图叫做零图，1阶零图叫做平凡图。所谓n阶图是指有n个顶点的图）。
可以视为函数空间的一个算子 
满足：
当 
是 
-正则图, 很容易得到：
其中 
是 
的邻接矩阵 , ( i. e., 
if 
is adjacent to 
, and 0 otherwise,) ， 
是一个单位矩阵. 这里所有矩阵的大小都是 
，其中 
图 
的定点数 .
对于一般图来说，
我们注意到
可以写成
其中 
是一个矩阵，其行由
的顶点索引，其列由的边索引 such that each column corresponding to an edge 
has an entry 
, in the row corresponding to 
, an entry
in the row corresponding to 
, and has zero entries elsewhere. (As it turns out, the choice of signs can be arbitrary as long as one is positive and the other is negative.) Also, 
denotes the transpose of 
.
For readers who are familiar with terminology in homology theory, we remark that 
can be viewed as a “boundary operator” mapping “1-chains” defined on edges (denoted by 
) of a graph to “0-chains” defined on vertices (denoted by 
). Then, 
is the corresponding “coboundary operator” and we have
Since 
is symmetric, its eigenvalues are all real and non-negative. We can use the variational characterizations of those eigenvalues in terms of the Rayleigh quotient of 
(see, e.g. [162]). Let 
denote an arbitrary function which assigns to each vertex u of a real value 
. We can view as a column vector. Then
where f
and 
denotes the sum over all unordered pairs 
for which 
and 
are adjacent. Here
denotes the standard inner product in 
. The sum 
is sometimes called the Dirichlet (狄利克雷) sum of 
and the ratio on the left-hand side of (1.1) is often called the Rayleigh quotient(瑞利商). (We note that we can also use the inner product
for complex-valued functions.
From equation (1.1) we see that all eigenvalues are non-negative. In fact, we can easily deduce from equation (1.1) that 0 is an eigenvalue of 
. We denote the eigenvalues of 
by 
. The set of the 
‘s is usually called the spectrum of 
(or the spectrum of the associated graph G
.) Let 1 denote the constant function which assumes the value 1 on each vertex. Then 
is an eigenfunction of 
with eigenvalue 0. Furthermore,
The corresponding eigenfunction is 
as in (1.1). It is sometimes convenient to consider the nontrivial function 
achieving (1.2), in which case we call 
a harmonic eigenfunction of 
.
The above formulation for 
corresponds in a natural way to the eigenvalues of the Laplace-Beltrami operator for Riemannian manifolds:
where 
ranges over functions satisfying
We remark that the corresponding measure here for each edge is 1 although in the general case for weighted graphs the measure for an edge is associated with the edge weight (see Section 1.4.) The measure for each vertex is the degree of the vertex. A more general notion of vertex weights will be considered in Section 2.5.
We note that (1.2) has several different formulations:
1.3
1.4
Where
and vol G denotes the volume of the graph , given by
By substituting for 
and using the fact that 2
, for 
we have the following expression (which generalizes the one in [126]):
1.5
Where 
denotes the sum over all unordered pairs of vertices 
in 
. We can characterize the other eigenvalues of 
in terms of the Rayleigh quotient. The largest eigenvalue satisfies:
1.6
For a general 
, we have
1.7
1.8
where 
is the subspace generated by the harmonic eigenfunctions corresponding to 
, for 
.
The different formulations for eigenvalues given above are useful in different settings and they will be used in later chapters. Here are some examples of special graphs and their eigenvalues.
Example 1.1.
For the complete graph on vertices, the eigenvalues are 0 and 
(with multiplicity 
).
Example 1.2.
For the complete bipartite graph on 
vertices, the eigenvalues are 0, 1 (with multiplicity 
), and 2.
Example 1.3.
For the star 
on vertices, the eigenvalues are 0,1 (with multiplicity n - 2
), and 2.
Example 1.4.
For the path 
on vertices, the eigenvalues are 
for 
.
Example 1.5.
For the cycle 
on vertices, the eigenvalues are for 
.
Example 1.6.
For the n-cube 
on 
vertices, the eigenvalues are 
(with multiplicity
for 
.
More examples can be found in Chapter 6 on explicit constructions.
1.3 Basic facts about the spectrum of Graph
Roughly speaking, half of the main problems of spectral theory lie in deriving bounds on the distributions of eigenvalues. The other half concern the impact and consequences of the eigenvalue bounds as well as their applications. In this section, we start with a few basic facts about eigenvalues. Some simple upper bounds and lower bounds are stated. For example, we will see that the eigenvalues of any graph lie between 0 and 2. The problem of narrowing the range of the eigenvalues for special classes of graphs offers an open-ended challenge. Numerous questions can be asked either in terms of other graph invariants or under further assumptions imposed on the graphs. Some of these will be discussed in subsequent chapters.
Lemma 1.7.
For a graph 
on 
vertices, we have
with equality holding if and only if 
has no isolated vertices.( 当且仅当
没有孤立顶点时，上式取等号。)
,
with equality holding if and only if 
is the complete graph on 
vertices.
Also, for a graph 
without isolated vertices, we have
(ⅲ): For a graph which is not a complete graph, we have 
.
(ⅳ): If 
is connected, then 
. If 
and 
, then 
has exactly
connected components.
(ⅴ): For all 
,we have
With λn-1=2
if and only if a connected component of G
is bipartite and nontrivial.
(ⅵ): The spectrum of a graph is the union of the spectra of its connected components.
For bipartite graphs, the following slightly stronger result holds:
Lemma 1.8.
The following statements are equivalent:
(i): 
is bipartite.
(ii): has 
connected components and 
for .
(iii): For each 
the value 
is also an eigenvalue of .
Lemma 1.9.
For a connected graph 
with diameter 
, we have
Lemma 1.10.
Let 
denote a harmonic eigenfunction achieving 
in (1.2). Then, for any vertex 
, we have
One can also prove the statement in Lemma 1.10 by recalling that 
, where 
Then
,
and examining the entries gives the desired result.
With a little linear algebra, we can improve the bounds on eigenvalues in terms of the degrees of the vertices.
We consider the trace of 
. We have
1.9
where
On the other hand,
1.10
where 
is the adjacency matrix. From this, we immediately deduce
Lemma 1.11.
For a 
-regular graph 
on n vertices, we have
1.11
This follows from the fact that
Let 
denote the harmonic mean of the 
’s, i.e.,
It is tempting to consider generalizing (1.12) with 
replaced by 
This, however, is not true as shown by the following example due to Elizabeth Wilmer.
Example 1.12.
Consider the 
-petal graph on 
vertices, 
with edges 
and
for 
, This graph has eigenvalues 0,1/2 (with multiplicity 
), and 2
(with multiplicity 
). So we have 
. However,
Still, for a general graph, we can use the fact that
1.2
Combining (1.10), (1.11) and (1.13), we obtain the following:
Lemma 1.13.
For a graph 
on n vertices, 
satisfies
where 
denotes the average degree of 
.
There are relatively easy ways to improve the upper bound for 
.From the characterization in the preceding section, we can choose any function 
, and its Rayleigh quotient will serve as an upper bound for 
. Here we describe an upper bound for 
(see [202]).
Lemma 1.14.
Let 
be a graph with diameter 
, and let 
denote the maximum degree of 
. Then
One way to bound eigenvalues from above is to consider "contracting" the graph 
into a weighted graph H (which will be defined in the next section). Then the eigenvalues of 
can be upper-bounded by the eigenvalues of H or by various upper bounds on them, which might be easier to obtain.
1.4 Eigenvalues of weighted graphs
Before defining weighted graphs, we will say a few words about two different approaches for giving definitions. We could have started from the very beginning with weighted graphs, from which simple graphs arise as a special case in which the weights are 0 or 1. However, the unique characteristics and special strength of graph theory is its ability to deal with the 
-problems arising in many natural situations. The clean formulation of a simple graph has conceptual advantages. Furthermore, as we shall see, all definitions and subsequent theorems for simple graphs can usually be easily carried out for weighted graphs. A weighted undirected graph 
(possibly with loops) has associated with it a weight function 
. Satisfying
And
We note that if 
, then 
. Unweighted graphs are just the special case where all the weights are 0 or 1.
In the present context, the degree 
of a vertex 
is defined to be:
We generalize the definitions of previous sections, so that
if u and v are adjacent, otherwise.
In particular, for a function 
we have
Let 
denote the diagonal matrix with the 
-th entry having value 
. The Laplacian of 
is defined to be
In other words, we have
We can still use the same characterizations for the eigenvalues of the generalized versions of L
. For example,
1.13
A contraction of a graph 
is formed by identifying two distinct vertices, say 
and , into a single vertex 
. The weights of edges incident to 
are defined as follows:
Lemma(引理) 1.15.
If 
is formed by contractions from a graph 
, then
1.5 Eigenvalues and random walks
In a graph 
, a walk is just a sequence of vertices 
with 
for all 
. A random walk is determined by the transition probabilities 
, which are independent of 
. Clearly, for each vertex 
,
For any initial distribution 
with 
, the distribution after k steps is just 
(i.e., a matrix multiplication with f viewed as a row vector where 
is the matrix of transition probabilities). The random walk is said to be ergodic if there is a unique stationary distribution 
satisfying
It is easy to see that necessary conditions for the ergodicity of 
are (i) irreducibility,i.e., for any 
, there exists some 
such that 
， (ii) aperiodicity i.e., g.c.d. 
. As it turns out, these are also sufficient conditions. A major problem of interest is to determine the number of steps s
required for Ps to be close to its stationary distribution, given an arbitrary initial distribution.
We say a random walk is reversible if
An alternative description for a reversible random walk can be given by considering a weighted connected graph with edge weights satisfying
where 
can be any constant chosen for the purpose of simplifying the values. (For example, we can take 
to be the average of 
over all 
with 
, so that the values for 
are either 0 or 1 for a simple graph.) The random walk on a weighted graph has as its transition probabilities
where 
is the (weighted) degree of 
. The two conditions for ergodicity are equivalent to the conditions that the graph be (i) connected and (ii) non-bipartite. From Lemma 1.7, we see that (i) is equivalent to 
and (ii) implies 
. As we will see later in (1.15), together (i) and (ii) deduce ergodicity.
We remind the reader that an unweighted graph has 
equal to either 0 or 1. The usual random walk on an unweighted graph has transition probability 
of moving from a vertex 
to any one of its neighbors. The transition matrix 
then satisfies
In other words,
For any 
It is easy to check that
where 
is the adjacency matrix.
In a random walk with an associated weighted connected graph 
, the transition matrix 
satisfies
where 1 is the vector with all coordinates 1. Therefore the stationary distribution is exactly 
, We want to show that when k is large enough, for any initial distribution 
, 
converges to the stationary distribution.
First we consider convergence in the 
(or Euclidean) norm. Suppose we write
where 
denotes the orthonormal eigenfunction associated with 
.
Recall that 
and 
denotes the 
- norm, so
since 
. We then have
G
2
2
1.14
Where
So, after
steps, the 
distance between 
and its stationary distribution is at most 
.
Although 
occurs in the above upper bound for the distance between the stationary distribution and the 
-step distribution, in fact, only 
is crucial in the following sense. Note that 
is either or 
. Suppose the latter holds, i.e., 
. We can consider a modified random walk, called the lazy walk, on the graph 
formed by adding a loop of weight dv to each vertex 
. The new graph has Laplacian eigenvalues 
, which follows from equation (1.14). Therefore,
and the convergence bound in 
distance in (1.15) for the modified random walk becomes
In general, suppose a weighted graph with edge weights 
has eigenvalues 
, with 
. We can then modify the weights by choosing, for some constant 
,
The resulting weighted graph has eigenvalues
where
Then we have
Since 
, and we have for 
. In particular we set
Therefore the modified random walk corresponding to the weight function 
has an improved bound for the convergence rate in 
distance:
We remark that for many applications in sampling, the convergence in distance seems to be too weak since it does not require convergence at each vertex. There are several stronger notions of distance several of which we will mention.
A strong notion of convergence that is often used is measured by the relative pointwise distance (see [225]): After s steps, the relative pointwise distance (r.p.d.) of P to the stationary distribution 
is given by
Let 
denote the characteristic function of x defined by:
Suppose
where 
’s denote the eigenfunction of the Laplacian 
of the weighted graph associated with the random walk. In particular,
Let A* denote the transpose of A. We have
where 
. So if we choose t such that
then, after t steps, we have 
When 
we can improve the above bound by using a lazy walk as described in (1.16). The proof is almost identical to the above calculation except for using the Laplacian of the modified weighted graph associated with the lazy walk. This can. be summarized by the following theorem:
Theorem(定理)1.16.
For a weighted graph 
, we can choose a modified random walk P so that the relative pairwise distance 
is bounded above by:
where 
and 
otherwise.
CORLOLLARY(推论) 1.17.
For a weight graphG
, we can choose a modified random walk P so that have
if
where and otherwise.
We remark that for any initial distribution 
with 
and
, we have, for any 
,
Another notion of distance for measuring convergence is the so-called total variation distance, which is just half of the 
distance:
The total variation distance is bounded above by the relative pointwise distance, since
Therefore, any convergence bound using relative pointwise distance implies the same convergence bound using total variation distance. There is yet another notion of distance, sometimes called 
-squared distance, denoted by 
and defined by:
using the Cauchy-Schwarz inequality. 
is also dominated by the relative pointwise distance (which we will mainly use in this book).
We note that
where 
denotes the projection onto the eigenfunction 
denotes the 
-th orthonormal eigenfunction of L and 
denotes the characteristic function of 
. Since
We have
1.16
Equality in (1.16) holds if, for example, 
is vertex-transitive, i.e., there is an automorphism mapping u to 
for any two vertices in 
, (for more discussions, see Chapter 7 on symmetrical graphs). Therefore, we conclude