谈谈互联网广告拍卖机制的发展:从GSP到DeepAuction
广告作为各互联网公司收入的大头,其拍卖机制设计因此也是关乎营收最为核心的方面。所谓的广告拍卖机制设计是指如何将有限的广告位分配给合适的广告,从而达到客户、平台以及用户三方的价值最优。
当前的广告拍卖被建模为暗拍的形式,即N个广告主分别以![]() 的出价来竞拍某个广告位
的出价来竞拍某个广告位![]() ,系统设计合适的分配策略(确定某个广告主获得广告位)以及计费策略(广告主应该被收多少钱)。
,系统设计合适的分配策略(确定某个广告主获得广告位)以及计费策略(广告主应该被收多少钱)。
1. GSP二价拍卖
对于上面我们讨论拍卖形式,很多同学很容易想到直接按价高者得,并按其出价计费,此时平台的收入应该是最大的,这种拍卖被称为一价拍卖,相关理论[1]表明当存在预算约束时,一价拍卖的期望收益要高于二价拍卖拍卖的期望收益。因此早期互联网广告(2004年以前)基本都是采取一价拍卖,因为当时互联网广告基本都是给某些大客户做的展示广告(按展现收费),甚至目前某些品牌展示广告也是按一价来计费的。
随着互联网发展,互联网的广告主越来越多,广告竞拍逐渐变成多轮密价拍卖,广告主之间不清楚各自的出价,但广告主可以通过多轮试探出价,从而找到一个合适出价,从而使得自身利益最大。但这种广告主反复试探出低,最终会使得整体平台出价降低,从而导致平台收益减少。
因此google在2004年推出了GSP拍卖[2],其认为一个稳定良好的拍卖机制应该满足激励兼容条件dominant strategy incentive compatible (DSIC):
- 客户如果按其真实心理价进行出价,那么其收益永远是最大的。
此外其还假设所有广告主是个体理性的individually rational (IR):
- 客户偏好收益最大化,同时其收益应该是大于0的
所谓的GSP拍卖,就是按价高者得,并按其后一位的出价来计费,这种方式其满足上述两个条件,会使客户都按真实出价,并达到纳什均衡。同时GSP拍卖的平台收益是较为均衡,客户理解较为简单,因此目前是最为主流的拍卖机制。
- 分配:
 ,价最高者胜出
,价最高者胜出 - 计费:
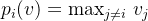 ,以次优者出价为计费
,以次优者出价为计费
2. VCG拍卖
虽然GSP拍卖对于多轮单次密价拍卖来说,平台收益是最优的,但是当同时拍卖多个广告位时,情况就不一样,假设同时存在二个广告位,如果是GSP拍卖,出价最高的将获得第一个广告位,并按第二高的出价计费,出价次高的将获得第二个广告位,并按第三高的出价计费。
但是因为广告主是同时对这两个广告位进行出价的,所以广告主一定偏好于第一个广告位么?如果第二个广告位的最终收益(价值-出价)大于第一个广告位的最终收益,此时广告主就倾向于出较低,此时将不满足激励兼容条件。
此外广告位不同位次之间相互关联影响也会降低平台整体拍卖效率,比如前一广告可能会影响后一位广告的点击率,以及一些整体广告展现体验限制(比如总体展示高度限制),当然这些问题通过某些打平手段可以部分解决。
VCG拍卖[3]提出一种针对于多位次拍卖最大化客户价值的最优机制:
- 分配:
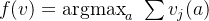 ,
, 表示广告位次某个组合,
表示广告位次某个组合,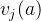 表示在页面组合某个广告的价值。广告直接分配给最大价值的广告组合,可以看出VCG拍卖是按整体广告展现页进行拍卖的。
表示在页面组合某个广告的价值。广告直接分配给最大价值的广告组合,可以看出VCG拍卖是按整体广告展现页进行拍卖的。 - 计费:
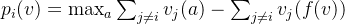 ,计费以不包含该广告的最大价值的广告组合减去剔除自身后广告组合价值,可以理解为该广告对于整体广告组合的边际价值。
,计费以不包含该广告的最大价值的广告组合减去剔除自身后广告组合价值,可以理解为该广告对于整体广告组合的边际价值。
VCG拍卖非常好的满足了激励兼容IC、个体理性IR条件,同时能最大化客户价值![]() ,但是VCG拍卖的计算量非常大(仅在4条广告2个广告位的情况下,就需要考虑
,但是VCG拍卖的计算量非常大(仅在4条广告2个广告位的情况下,就需要考虑![]() 种页面组合的情况)。同时VCG拍卖规则相对比较复杂,对于客户分析以及理解较难(比如客户出价最高但并没有胜出)。
种页面组合的情况)。同时VCG拍卖规则相对比较复杂,对于客户分析以及理解较难(比如客户出价最高但并没有胜出)。
当然最大的问题其并不能保证平台收益最优的,甚至在多数情况下相比于GSP,其平台收入是有损的,因此当前多数互联网公司基本都是以GSP为基础拍卖机制。
3. Myerson拍卖
是否存在一种拍卖机制能实现平台收益最大,Myerson拍卖[4]提出了一种在单物品密价拍卖情况下平台收益最优的拍卖机制。Myerson拍卖极为复杂,其实现大概分成如下步骤
- 修正价值c:
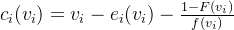 ,此处的
,此处的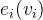 表示该客户价值对于其他客户心理价价值的影响,可以证明
表示该客户价值对于其他客户心理价价值的影响,可以证明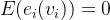 ,同时当所有客户心理价值是严格对称时
,同时当所有客户心理价值是严格对称时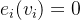 ,
,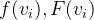 分别表示客户价值分布概率密度函数以及累积密度函数。
分别表示客户价值分布概率密度函数以及累积密度函数。 - 分配:
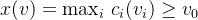 ,修正价值最高者胜出(同时修正价要大于平台保留价)
,修正价值最高者胜出(同时修正价要大于平台保留价) - 计费:
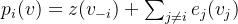 ,其中下式
,其中下式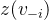 ,反映了修正价值的边际值。
,反映了修正价值的边际值。
Myerson拍卖从理论上证明其在保证激励兼容IC、个体理性IR等条件下达到平台收益最优,但最大问题是平台必须获得客户价值分布概率密度函数以及累积密度函数![]() ,同时概率密度函数也必须满足一定条件。
,同时概率密度函数也必须满足一定条件。
但是实际工程应用中很难获得客户价值分布的估计,因此极少有平台直接采用Myerson拍卖,但是Myerson修正价值c可以视为某个保留价策略,因此部分公司主要将Myerson拍卖用作某个保留价策略,特别是同VCG拍卖相结合,可以减少了VCG拍卖对于平台收益的损失,也有相关理论表明保留价可以保证平台收益下界。
4. 智能出价
到了17年左右开始,互联网广告有了重大改变,主要是智能出价产品(其在不同公司可能会被称为自动出价、oCPC、eCPA、CPA、ROI等等)取代了原有按点击计费的出价产品(CPC)成为各厂的主流。所谓的智能出价是指客户直接根据其营销目标给出约束,由平台自动帮其在流量维度进行出价,这种方式极大地提高了广告主投放效率,同时使其整体营销成本更可控,我们能游戏广告主为例,比较多种不同类型智能出价和CPC出价的不同:
- 按用户点击计费(CPC):客户按流量、关键词、人群等进行出价,最终平台按点击量*平均点击价格计费。
- 按用户下载计费(智能出价):客户设置整体的下载营销成本,最终平台按游戏下载量*客户设置的下载营销成本收费
- 按用户注册计费(智能出价):客户设置整体的拉新注册营销成本,最终平台按游戏下载量*客户设置的营销成本收费
- 按营销ROI计费(智能出价):客户设置整体广告投放ROI(广告主为投放广告所花费的总金额/广告所吸引用户为广告主所带来的总价值),最终平台按为广告主所带来的总价值*客户设置整体广告投放ROI进行收费
可以看出智能出价对广告主投放效率提升,另外从平台角度上,平台有更大空间来控制系统的拍卖,同时平台收益同客户收益也能达成双赢,比如对于按用户注册计费(智能出价),客户目标是为了尽可能多的提升注册量,同时平台也会尽可能多的提升注册量以达到收入最大化。
google在17年针对于各类智能出价提出了一种通用性的框架[5],其将智能出价建模为一个线性规划问题
并推导出智能出价的最优形式(如下),同时设计了一个相当复杂的大规划线性规划求解器来计算公式里的参数。
对于一个相对稳定的系统来说,直接通过上述方法确实是最优的,但是在实际工程中,由于竞争环境乃至客户自身变化,会导致数据分布不一致,也就说通过历史数据计算的出价参数不能很好的适应当前的环境。因此为了更好的满足客户约束,会在上述出价基础上,会额外添加控制模块,实现实时控制出价满足客户约束,目前主流的方法有两种:
- PID控制:PID作为传统的控制算法,其主要的优点是易用以及稳定,但是控制模块的目标是要求在特定窗口(比如天级)保证客户转化成本是稳定,原生的PID是不能保证达成的,一般会有如下几点需要额外调整:
- 对于当前置信度的判断:比如在某个时刻发生成本未达成,是否是由于波动(未来会达成),如果是异常,这个程度有多大?需要干预多少?这问题可以通过一些比如贝叶斯先验估计、长短时间窗口等方法来解决部分。
- 对于未来的判断:以自然天窗口的控制为例,早上超成本同晚上超成本应该是不同。需要考虑作用控制后对于未来的影响,特别是添加控制后,客户是否会完全停滞消费?
- 小客户的天然波动:小客户由于转化量级很少,因此其分天的实际转化成本也会存在波动,这个波动是通过出价无法控制,因此一些bank account策略会从计费上去调整来保证其成本的稳定性。
- 强化学习:阿里在近年来提出了一系列基于强化学习的自动出价控制算法[6]。其将自动出价建模为一个带约束马尔可夫决策过程Constraint MDP,每个广告拥有一个决策模型,决策模型根据剩余时间、剩余预算、预算消耗速率等元素组成状态来产出具体出价(动作),奖励函数和约束函数分别是表示当前累积优化目标以及约束达成情况。强化学习相比于PID控制,从理论上建模更为完整优雅,但是其实现相对比较复杂,同时对于长尾广告主效果稳定性是一个问题。
此外也有部分公司并不是按基础出价+成本控制的模式,而是将两者合并为一个出价模块,不同的智能化出价产品对应不同出价模块,这种方式相比于前者,整体实现和计算都较为复杂,好处是不同的智能化出价产品能相互解耦,此外为了保证整体出价模块的稳定性,可以更为方便地进行出价退化,比如当ROI出价有异常时,可以直接调用CPA出价,这种退化可以避免客户效果不会太差。
智能出价对于客户来说确实是好事,但对于平台来说一定会好吗?首先从本质上看,智能出价有点类似于一价拍卖,此时平台必然不是激励兼容了,但对于平台收益会有什么样的影响?
google给出了一篇理论文章[7],其证明了通过添加boost以及保留价,可以得出了在智能出价上平台收益和客户价值的下界,因此添加boost以及保留价能保证平台收益和客户价值的稳定性,具体也可以参考这篇文章的分析。
5. Deepauction
现在对于广告平台来说,有没有办法可以同时做平台收益以及激励兼容吗?google在17年提出了一种通过深度神经网络方式来完成广告拍卖和计费。
其将客户的出价作为auction模型的输入,其loss主要有三部分:平台收益、rgt客户不按真实出价的惩罚项以及增广拉格朗日正则项。
通过深度模型完全将拍卖机制建模为一个黑盒模式,但其通过一些实验表明其可以达成myerson等最优拍卖机制类似的效果。 google在该文中提出的模型结构相比比较简单,还存在某些研究将transformer等结构引入[9],其还通过实验表明其模型相比于myerson等传统拍卖机制在多物品拍卖上有更高的收益。
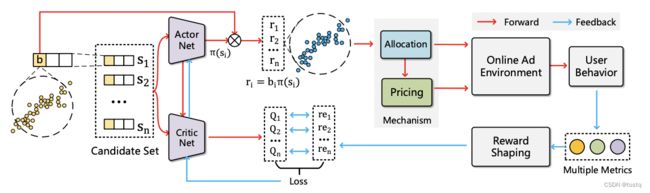
受google工作的启发,阿里提出了自己deepauction模型,20年提出的DeepGSP[10]通过深度强化学习,除了强化学习本身的范式不同,其同google的模型的不同之处还有三个地方:
- DeepGSP主要是通过强化学习模型计算分配概率(rank score)
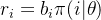 ,因此其分配和计费仍是传统GSP模式:
,因此其分配和计费仍是传统GSP模式:
- 分配:
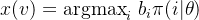
- 计费:
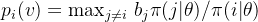
- 分配:
- 激励兼容保证:google模型的单调性是通过regret网络来保证的,而DeepGSP是通过两点:
- 分配公式中
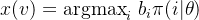 ,出价bid同分配是正相关的,同时也满足
,出价bid同分配是正相关的,同时也满足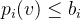
- 添加单调性loss来保证整体出价bid同分配胜出概率是正相关的,即
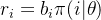 关于出价梯度应该是正向的。
关于出价梯度应该是正向的。
- 分配公式中
- 优化目标:DeepGSP并不只是为了最大平台收益,其是为了解决多目标优化,或者说其优化的loss中除了平台收益,还包含了GMV等部分。
也许是强化学习方式太过复杂,阿里在21年提出直接监督学习方式Neural Auction[11],该方法相比于前者,还有一个很大的不同在于,其将bid完全融入到了rank score计算的模型,或者说模型产出rankscore同bid并没有显式表达关系。
也许是担心通过loss来控制激励兼容不太可控,因此Neural Auction通过min-max网络将bid同rankscore之间计算参数通过![]() 方式固定为大于0的值,另外min-max网络也可以非常方便的支持计费反解(min-max网络的本质是多种线性公式的组合)。
方式固定为大于0的值,另外min-max网络也可以非常方便的支持计费反解(min-max网络的本质是多种线性公式的组合)。
总体来说阿里的这几篇工作的研究相当不错, 从论文上看其效果提升很明显,便是抛开多目标优化这种不谈,特别是DeepGSP其本质上是根据后验对点击率预估作为了重新校正,其同google的最优化收益是有不同,因此在阿里之后,国内多家公司在跟进尝试后发现效果并没有很大提升,所以笔者猜测可能这几点原因。
- 后验点击同出价有某种关系,这种关系之前点击率预估并没有学习
- 其他的后验多目标指标存在复杂的相互关系,这个关系针对于不同场景是不同的。
因此不同公司各自投放系统不同,并不一定能完全适配。此外近期阿里还提出了更为激进的完全端到端的拍卖系统,将上述的智能出价以及拍卖机制完全融入到了一个模型里。
而且随着大规模语言模型LLM的火热,部分公司开始构想所谓的生成式广告系统,广告主完全不需要设计任何创意、文案、配图甚至落地页,平台将自动生成最优的广告,这种生成式广告形式将传统系统中分开的创意生成、点击率预估、转化率预估、拍卖机制等多个模块合并为一个生成式模型,这种方式极大地降低了广告主营销成本以及平台人效成本,但作为广告营销人员以及产研人员未来将何去何从也是一个问题,不过好消息是今年还是能正常过日子的。。。>_<||
参考文献
[1] 克里斯纳. 拍卖理论[M]. 格致出版社, 2012. p41
[2] BFO Mills, BRL Dewey, BJ Lindeman. The American Economic Review[J]. American Economic Associ, 2006.
[3] HAL, R, VARIAN, et al. The VCG Auction in Theory and Practice[J]. The American Economic Review, 2014.
[4] Myerson R B . Optimal Auction Design[J]. Discussion Papers, 1981, 6(1):58-73.
[5] Aggarwal, G., Badanidiyuru, A., Mehta, A. (2019). Autobidding with Constraints. In: Caragiannis, I., Mirrokni, V., Nikolova, E. (eds) Web and Internet Economics. WINE 2019. Lecture Notes in Computer Science(), vol 11920. Springer, Cham.
[6] Zhao J , Qiu G , Guan Z , et al. Deep Reinforcement Learning for Sponsored Search Real-time Bidding[J]. ACM, 2018.
[7] Balseiro S , Deng Y , Mao J , et al. Robust Auction Design in the Auto-bidding World[J]. 2021.
[8] Dütting P, Feng Z, Narasimhan H, et al. Optimal auctions through deep learning[C]//International Conference on Machine Learning. PMLR, 2019: 1706-1715.
[9] Zhijian Duan Jingwu Tang Yutong Yin Zhe Feng Xiang Yan Manzil Zaheer Xiaotie Deng . a context integrated transfonner based neura1 network for auction design[J]. 2022.
[10] Zhang Z, Liu X, Zheng Z, et al. Optimizing Multiple Performance Metrics with Deep GSP Auctions for E-commerce Advertising[C]//Proceedings of the 14th ACM International Conference on Web Search and Data Mining. 2021: 993-1001.
[11] Liu X, Yu C, Zhang Z, et al. Neural auction: End-to-end learning of auction mechanisms for e-commerce advertising[C]//Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. 2021: 3354-3364.