三元组顺序表稀疏矩阵加法实现A+B,不增加A,B之外的储存空间,O(m+n)的时间复杂度
三元组顺序表加法实现A+B,不增加A,B之外的储存空间,O(M+N)的时间复杂度
- 参考链接
- 先定义需要用到类
- 接下来便是算法的主体部分了(略微冗长)
- 方法二 (效率较低的版本)
参考链接
链接: https://blog.csdn.net/weixin_34355881/article/details/85808635.
#这个算法我是看这个博客上的,不过那里是图片,使用c实现,需要看原代码的话是在这里的5.22题,算法主体几乎一样
先定义需要用到类
这个是用c++定义的两个类,分别是三元组节点和矩阵,这里的成员函数我就不分开写了,也不是很多
using eleType = int;
const int maxsize = 100;
class triple
{
public:
int row, col;
eleType ele;
triple(int row,int col,eleType ele):row(row),col(col),ele(ele){}
triple():row(0), col(0), ele(0) {}
};
bool operator==(const triple& a,const triple& b) { return (a.row == b.row && a.col == b.col); } //仅用来判断序号是否相等,不判断元素值
这里面写了几种这个矩阵的初始化方式,等会方便测试使用,但是并没有很严格的逻辑,但是测试够用了
class TSMatrix
{
public:
triple data[maxsize + 1];
int row, col, len;
TSMatrix(int row, int col, int len = 0) :row(row), col(col), len(len) {} //默认长度为零,每插入一个加一
TSMatrix() :row(0), col(0), len(0) {}
TSMatrix(const TSMatrix& tsm) :row(tsm.row), col(tsm.col), len(tsm.len)
{
for (int i = 0; i < tsm.len; i++)
data[i] = tsm.data[i];
}
TSMatrix(triple trp[], int eleNum) //用数组来初始化矩阵,elenum表示初始化的元素个数
{
len = eleNum;
row = 0; col = 0;
for (int i = 0; i < eleNum; i++)
{
data[i] = trp[i];
if (trp[i].row > row) //取出这几个元素中的行和列的最大值,
row = trp[i].row;
if (trp[i].col> col)
col = trp[i].col;
}
}
ostream& print(ostream& os = cout) const
{
int dataindex = 0;
for (int i = 0; i <= row; i++)
{
for (int j = 0; j <= col; j++)
{
if (i == data[dataindex].row && j == data[dataindex].col)
{
cout << data[dataindex].ele << '\t';
dataindex++;
}
else
cout << "0\t";
}
cout << endl;
}
return os;
}
};
ostream& operator<<(ostream& os, const TSMatrix& tmp) { return tmp.print(os); }
接下来便是算法的主体部分了(略微冗长)
bool TSMadd(TSMatrix& A, TSMatrix B)
{
if (A.col != B.col || A.row != B.row) //矩阵格式不相等退出
{
cout << "两个相加矩阵的格式错误" << endl;
return 0;
}
int m(B.len), n(0), k(-1);
for (int i = A.len-1; i >=0; i--) //把A中的元素往后移B.len个位置
{
A.data[i + B.len] = A.data[i];
}
while (m < A.len + B.len && n < B.len) //进行A和B的元素的遍历
{
if (A.data[m].row < B.data[n].row) //外层的row比较
A.data[++k] = A.data[m++];
else if (A.data[m].row > B.data[n].row)
A.data[++k] = B.data[n++];
else //若row相等则再比较col
{
if (A.data[m].col < B.data[n].col)
A.data[++k] = A.data[m++];
else if (A.data[m].col > B.data[n].col)
A.data[++k] = B.data[n++];
else
{
if (A.data[m].ele + B.data[n].ele) //这里要注意的是假如两者元素相加为0,意味着这个值不能存起来,因为三元组里只储存非零值
{
k++;
A.data[k].col = A.data[m].col;
A.data[k].row = A.data[m].row;
A.data[k].ele = A.data[m].ele + B.data[n].ele;
}
m++; //这里就是为零的情况
n++;
}
}
}
while (m < A.len + B.len)
A.data[++k] = A.data[m++];
while (n < B.len)
A.data[++k] = B.data[n++];
A.len = k;
return 1;
}
他这里的逻辑不会很难,主要就是把A和B的元素有row到col进行比较,外层循环是比对row,内层循环是比对col,谁小谁排前面,然后比较后的结果的存储在A中,这也就是为什么。
最后的两个while是因为A或者B都有可能没有比较完全,这意味着可能在A这个序列里面
接下来是测试代码
int main()
{
triple data1[6] = { {0,1,1},{0,2,2},{1,2,3}, {3,6,6},{4,1,2},{5,6,8} }; //这里的顺序必须合法,因为以下的初始化当中没有为它自动排序的功能
triple data2[7] = { {0,1,1},{0,2,-2},{1,2,3},{2,5,6}, {3,6,-6},{4,1,2},{5,6,-6} };
TSMatrix tsm1(data1, 6);
TSMatrix tsm2(data2, 7);
TSMatrix tsm3(tsm1);
cout << tsm3;
cout << "***分割线***" << endl;
TSMadd(tsm3,tsm2);
cout << tsm3;
system("pause");
}
这个是运行的结果。
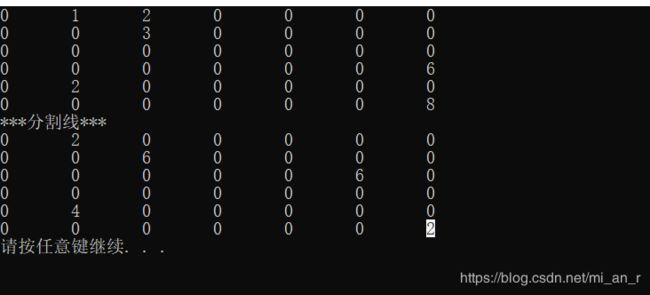
然后接下来的是自己一开始写的时候的思路,复杂度要大,应该是O(m*n)
但是要简单一些,通过调用插入的这个函数,这个函数既可以用作修改,也可以用作初始化
方法二 (效率较低的版本)
首先实现定义一个枚举量,因为这个插入函数有不同的两种作用,可以用作普通插入,亦可用来做加法
enum mode {insert, add};
void TSMtrInsert(TSMatrix& tsm, triple trp, mode m = insert) //默认情况下就是插入
{
int i = 0;
for (; i < tsm.len; i++)
{
if (tsm.data[i].row == trp.row && tsm.data[i].col == trp.col) //倘若插入的元素位置重合
{
if(m == insert) //替换掉原来的元素值,然后退出
tsm.data[i].ele = trp.ele;
else if(m == add) tsm.data[i].ele += trp.ele; // 相加后退出
return;
}
//否则取到这个插入位置
if(trp.row < tsm.data[i].row)
break;
if (trp.row == tsm.data[i].row && trp.col < tsm.data[i].col)
break;
}
for (int j = tsm.len; j > i; j--) //这个位置后的元素后移一位,然后插入
{
tsm.data[j] = tsm.data[j - 1];
}
tsm.data[i] = trp;
tsm.len++;
}
之后便是重载加号
TSMatrix operator+(const TSMatrix& a,const TSMatrix& b)
{
TSMatrix c(a);
if (a.col != b.col || a.row != b.row) //矩阵格式不相等退出
{
cout << "两个相加矩阵的格式错误" << endl;
return c;
}
c.col = a.col; c.row = c.row;
for (int i = 0; i < b.len; i++)
TSMtrInsert(c, b.data[i], add);
return c;
}
测试函数如下
int main()
{
triple data1[6] = { {0,1,1},{0,2,2},{1,2,3}, {3,6,6},{4,1,2},{5,6,8} }; //这里的顺序必须合法,因为以下的初始化当中没有为它自动排序的功能
triple data2[7] = { {0,1,1},{0,2,-2},{1,2,3},{2,5,6}, {3,6,-6},{4,1,2},{5,6,-6} };
TSMatrix tsm1(data1, 6);
TSMatrix tsm2(data2, 7);
TSMatrix tsm3 = tsm1 + tsm2;
cout << tsm3;
system("pause");
}
这个此的内容就到这了,内容很普通,没啥高级算法,有一些错误在所难免,有的话请指正。