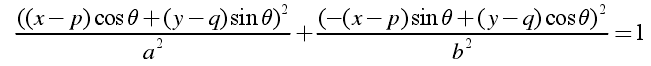QT+opencv学习笔记(5)——霍夫直线检测、圆检测及椭圆检测
开发环境为:win10+QT5.8+opencv3.2
Hough变换是图像处理中从图像中识别几何形状的基本方法之一,应用很广泛。最基本的Hough变换是从黑白图像中检测直线,还可以经过改进检测圆、椭圆、正方形等。本文主要实现Hough直线检测、Hough圆检测、Hough椭圆检测。
一、读取图像
读取图像见QT+opencv学习笔记(1)——图像点运算,这里不再赘述。
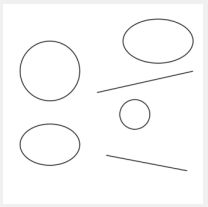
读取结果如下图:
二、Hough直线检测
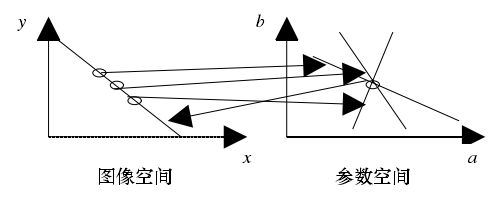
使用Hough变换进行直线检测, 首先要从原始图像中提取出边缘信息, 将原图转换成一个二值化的边缘轮廓图, 然后将这个二值边缘图中的采样点映射到Hough参数空间中的直线b=-xa+y, 在参数空间中绘制出直线后,在每一个点上进行统计,点的数值代表参数空间中穿过该点直线的数目。如图1-1所示, 由于图像空间中的点对应于参数空间中的直线, 而图像空间中的直线相应地对应于参数空间中的点, 因此在二维累加器中统计各点数值后所找到超过一定阈值的峰值点就是图像空间中的直线。
图1-1直线Hough变换的对应关系
在具体操作中,通常使用直线的法线式。因为当直线平行于纵轴时,直线方程 y=ax+b中参数a趋于无穷大,无法在参数空间中进行统计,而使用直线的法线式可以检测出这类直线。图像空间x-y中的直线法线式如下:
其中,ρ为直线L到原点的距离;θ为直线 L与x轴正方向的夹角,根据上式,直线L 上不同的点在参数平面ρ-θ中被变换为一簇相交于t点的正弦曲线。显然,若能确定参数平面中的t点,就实现了直线检测。在实际计算中,根据图像空间中的数据点计算Hough 参数空间中的正弦曲线轨迹,在参数平面上进行二维统计,选取峰值。该峰值就是图像空间中一条直线的参数,从而实现了图像空间中的直线检测。
在opencv中分别有HoughLines()函数和HoughLinesP()函数可以实现Hough直线检测。
HoughLines()函数实现方式为标准霍夫变换。标准霍夫变换本质上是把图像映射到它的参数空间上,它需要计算所有的M个边缘点,这样它的运算量和所需内存空间都会很大。 HoughLines()函数定义如下:
void HoughLines(InputArray image, //8位单通道二值图像,函数可能会修改输入图像,所以不要使用原图
OutputArray lines, //输出直线向量,两个元素的向量(ρ,θ)代表一条直线,ρ是从原点(图像的左上角)的距离
//θ是直线的角度(单位是弧度),0表示垂直线,π/2表示水平线
double rho, //距离分辨率
double theta, //角度分辨率
int threshold, //阈值,只有大于该值的点在霍夫空间变换中才有可能被当作极大值
double srn=0, //用于多尺度霍夫变换
double stn=0 ) //用于多尺度霍夫变换主要代码如下:
Canny( srcImg, lineImg, 50, 200, 3 );
cvtColor( lineImg, color_lineImg, CV_GRAY2BGR );
vector lines;
HoughLines( lineImg, lines, 1, CV_PI/180, 100 );
for( size_t i = 0; i < lines.size(); i++ )
{
float rho = lines[i][0];
float theta = lines[i][1];
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
Point pt1(cvRound(x0 + 1000*(-b)),
cvRound(y0 + 1000*(a)));
Point pt2(cvRound(x0 - 1000*(-b)),
cvRound(y0 - 1000*(a)));
line( color_lineImg, pt1, pt2, Scalar(0,0,255), 3, 8 );
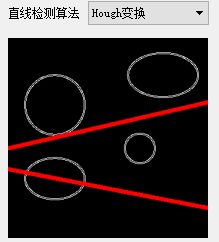
} 霍夫变换直线检测结果如下:
如果在输入图像中只是处理m(m
HoughLinesP函数就是利用概率霍夫变换来检测直线的。它的一般步骤为:
1、随机抽取图像中的一个特征点,即边缘点,如果该点已经被标定为是某一条直线上的点,则继续在剩下的边缘点中随机抽取一个边缘点,直到所有边缘点都抽取完了为止;
2、对该点进行霍夫变换,并进行累加和计算;
3、选取在霍夫空间内值最大的点,如果该点大于阈值的,则进行步骤4,否则回到步骤1;
4、根据霍夫变换得到的最大值,从该点出发,沿着直线的方向位移,从而找到直线的两个端点;
5、计算直线的长度,如果大于某个阈值,则被认为是好的直线输出,回到步骤1。
HoughLinesP()函数定义如下:
void HoughLinesP(InputArray image, //8位单通道二值图像,函数可能会修改输入图像,所以不要使用原图
OutputArray lines, //输出的直线向量,每条线用4个元素表示,即直线的两个端点的4个坐标值
double rho, //距离分辨率
double theta, //角度分辨率
int threshold, //阈值,它表示要判断为一条直线所需的最少度量,显然这个值越大,
//所判断出的直线越少;这个值越小,所判断出的直线越多。
double minLineLength=0, //根据threshold提取出的直线长短不一,这个参数以长度对这些直线作一次筛选,
//小于这个参数值的就被抛弃。显然这个值越大,所判断出的直线越少;这个值越小,所判断出的直线越多。
double maxLineGap=0 //最大直线间隙,即如果有两条线段在一条直线上,但它们之间因为有间隙,所以被认为是两个线段,
//如果这个间隙大于该值,则被认为是两条线段,否则是一条。显然这个值越大,所判断出的直线越少;
//这个值越小,所判断出的直线越多(值越小,那么间隙值就越容易大于这个值)。
)主要代码如下:
Canny( srcImg, lineImg, 50, 200, 3 );
cvtColor( lineImg, color_lineImg, CV_GRAY2BGR );
vector lines;
HoughLinesP( lineImg, lines, 1, CV_PI/180, 80, 30, 10 );
for( size_t i = 0; i < lines.size(); i++ )
{
line( color_lineImg, Point(lines[i][0], lines[i][1]),
Point(lines[i][2], lines[i][3]), Scalar(0,0,255), 3, 8 );
}
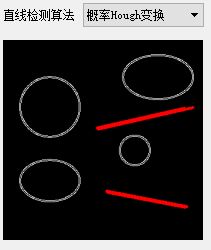
//imshow( "Detected Lines", color_lineImg ); 概率霍夫变换直线检测结果如下:
三、Hough圆检测
霍夫圆检测的基本原理霍夫直线检测类似, 只是点对应的二维极径极角空间被三维的圆心点x, y还有半径r空间取代。
对直线来说, 一条直线能由参数极径极角 (r, θ) 表示。而对圆来说, 我们需要三个参数来表示一个圆, 现在原图像的边缘图像的任意点对应的经过这个点的所有可能圆是在三维空间有下面这三个参数来表示了,其对应一条三维空间的曲线。那么与二维的霍夫线变换同样的道理, 对于多个边缘点越多这些点对应的三维空间曲线交于一点那么他们经过的共同圆上的点就越多,类似的我们也就可以用同样的阈值的方法来判断一个圆是否被检测到, 这就是标准霍夫圆变换的原理, 但也正是在三维空间的计算量大大增加的原因, 标准霍夫圆变化很难被应用到实际中。
出于上面提到的对运算效率的考虑, OpenCV实现的是一个比标准霍夫圆变换更为灵活的检测方法: 霍夫梯度法, 也叫2-1霍夫变换(21HT), 它的原理依据是圆心一定是在圆上的每个点的模向量上, 这些圆上点模向量的交点就是圆心, 霍夫梯度法的第一步就是找到这些圆心, 这样三维的累加平面就又转化为二维累加平面. 第二步根据所有候选中心的边缘非0像素对其的支持程度来确定半径。霍夫圆检测可以通过HoughCircles()函数来实现。
HoughCircles()函数定义如下:
void HoughCircles(InputArray image, //8位单通道灰度图
OutputArray circles, //找到的圆的输出向量,每个向量用(x, y, radius)来表示
int method, //检测方法CV_HOUGH_GRADIENT,现在OpenCV中只有霍夫梯度法
double dp, //累加器分辨率相对于图像分辨率的比率
double minDist, //检测出的圆心之间的最小距离
double param1=100, //Canny边缘函数的高阈值
double param2=100, //检测圆心的累加器的阈值
int minRadius=0, //最小圆半径
int maxRadius=0 //最大圆半径
) 主要代码如下:
Mat grayImg = srcImg.clone();
Mat colorImg;
cvtColor(grayImg, colorImg, CV_GRAY2BGR);
//平滑图像
GaussianBlur( grayImg, grayImg, Size(9, 9), 2, 2 );
vector circles;
HoughCircles(grayImg, circles, CV_HOUGH_GRADIENT,
2, grayImg.rows/4, 200, 150 );
for( size_t i = 0; i < circles.size(); i++ )
{
Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
int radius = cvRound(circles[i][2]);
//绘制圆心
circle( colorImg, center, 3, Scalar(0,255,0), -1, 8, 0 );
//绘制圆的边
circle( colorImg, center, radius, Scalar(0,0,255), 3, 8, 0 );
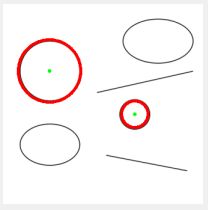
} Hough圆检测处理结果如下:
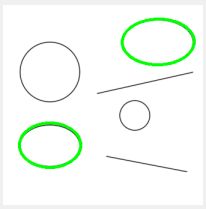
四、Hough椭圆检测
椭圆几何定理:设平面上有一个椭圆,点c为椭圆圆心,任取平面上一点p(不同于点c),点p距椭圆上点的最大距离一定大于点 c距椭圆上点的最大距离。
下面介绍所采用的椭圆检测方法。其指导思想是利用上面的椭圆几何定理,通过查找距离椭圆上点最大距离最小的点来找到圆心,同时这个最小的最大距离就是椭圆的长轴长度。通过这种方法,椭圆的5个参数(椭圆圆心点横、纵坐标,长、短轴长,旋转角度)得到了3个,剩下的2个参数就可以在二维参数空间上统计了,即可以采用Hough变换检测直线的相同方法来检测椭圆了。
算法的具体操作步骤如下:
(1)对要处理的图像进行边缘检测,得到二值化的边缘轮廓图,将边缘图上的点存入数组A。
(2)对二维平面上的每一点,计算与上一步所得数组A中点的距离,得到每一点距数组A 中点的最大距离,所有点中最大距离最小的点即是椭圆圆心(p,q),该最大距离即是椭圆长轴长度 a。
(3)将数组A中每一点的数值和刚才得到的3个椭圆参数p、q、a代入椭圆方程E:
主要代码如下:
Mat grayImg = srcImg.clone();
Mat colorImg;
cvtColor(grayImg, colorImg, CV_GRAY2BGR);
GaussianBlur(grayImg, grayImg, Size(3,3), 0, 0); //高斯平滑
Canny(grayImg, grayImg, 100, 200, 3); //Canny边缘检测
namedWindow("Canny", CV_WINDOW_AUTOSIZE);
imshow("Canny", grayImg);
//提取轮廓
vector> contours;
vector hierarchy;
findContours(grayImg,contours,hierarchy,CV_RETR_EXTERNAL,CV_CHAIN_APPROX_NONE);
//绘制查找到的轮廓
//drawContours(colorImg, contours, -1, Scalar(0,255,0));
//imshow("cour.bmp",colorImg);
//Hough变换
int accumulate; // Hough空间最大累积量
Ellipse myellipse;
Mat elliImg(grayImg.size(),CV_8UC3,Scalar(0));
for(int i=0;i< contours.size();i++)
{
myellipse.Computer_axy(contours[i],grayImg.size());
accumulate=myellipse.hough_ellipse(contours[i]);
//cout<<"accumulate:"<=contours[i].size()*0.25 && abs(myellipse.getLongAxis()-myellipse.getShortAxis())>2.0
&& abs(myellipse.getLongAxis()-myellipse.getShortAxis())<50.0)
elliImg=myellipse.draw_Eliipse(colorImg);
} 整体工程代码见QT+opencv霍夫直线检测,圆检测及椭圆检测
参考:
(1)OpenCV霍夫系列(后篇)-统计概率霍夫变换(HoughLinesP)
(2)opencv 霍夫圆检测
(3)Hough变换检测椭圆 附带matlab与opencv代码