Datawhale组队学习 Task2-数据分析
数据分析内容概览
- 1. 数据载入及总览
- 1.1 载入各种数据科学以及可视化库
- 1.2 载入数据
- 1.3 总览数据
- 1.3.1 head()+shape观察数据
- 1.3.2 describe()熟悉相关统计量
- 1.3.3 info()熟悉数据类型
- 2. 判断缺失和异常
- 2.1 缺失值
- 2.2 异常值
- 3. 了解预测值分布
- 3.1 总体分布概况
- 3.1.1 为什么要转化为正态分布
- 3.1.2 样本不服从正态分布怎么办
- 3.1.3 和无界约翰逊分布有什么关系
- 3.1.4 本文中的变换
- 3.2 查看偏度(Skewness)和峰度(Kurtosis)
- 3.3 查看预测值频数
- 4. 特征分析
- 4.1 数字特征
- 4.1.1 相关性分析
- 4.1.2 查看特征偏度和峰值
- 4.1.3 每个数字特征的分布可视化
- 4.1.4 匿名特征分布情况
- 4.1.5 多变量与price的回归关系
- 4.2 类别特征
- 4.2.1 查看nunique分布
- 4.2.2 查看箱型图
- 4.2.3 查看小提琴图
- 4.2.4 查看柱形图
- 4.2.5 类别频数可视化
- 5. 生成数据报告
- 6. 收获及未来工作
- 6.1 收获
- 6.2 未来工作
1. 数据载入及总览
1.1 载入各种数据科学以及可视化库
- missingno库用于可视化缺失值分布,是基于matplotlib的,接受pandas数据源
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno # 用于可视化缺失值分布
import scipy.stats as st
1.2 载入数据
注:所有特征集均脱敏处理,脱敏处理后均为label encoding形式,即数字形式
| Field | Description |
|---|---|
| SaleID | 交易ID,唯一编码 |
| name | 汽车交易名称,已脱敏 |
| regDate | 汽车注册日期 |
| model | 车型编码 |
| brand | 汽车品牌 |
| bodyType | 车身类型 |
| fuelType | 燃油类型 |
| gearbox | 变速箱 |
| power | 发动机功率 |
| kilometer | 汽车已行驶公里 |
| notRepairedDamage | 汽车有尚未修复的损坏 |
| regionCode | 地区编码 |
| seller | 销售方 |
| offerType | 报价类型 |
| creatDate | 汽车上线时间 |
| price | 二手车交易价格 |
| v系列特征 | 匿名特征,包含v0-14在内15个匿名特征 |
path = './data/'
Train_data = pd.read_csv(path+'used_car_train_20200313.csv', sep=' ')
Test_data = pd.read_csv(path+'used_car_testA_20200313.csv', sep=' ')
1.3 总览数据
1.3.1 head()+shape观察数据
要养成看数据集的haed()和shape的习惯,让每一步都更放心
Train_data.head().append(Train_data.tail())
Test_data.head().append(Test_data.tail())
print('Train data shape:', Train_data.shape)
print('TestA data shape:', Test_data.shape)
1.3.2 describe()熟悉相关统计量
- describe()中包含每列的统计量,个数(count)、平均值(mean)、方差(std)、最小值(min)、中位数(25% 50% 75%)、最大值(max)
- 通过观察以上指标,可以瞬间掌握数据的大概范围 和 每个值异常值的判断 ,例如有时候会发现999 9999 -1 等值这些其实都是nan的另外一种表达方式,需注意
print(Train_data.describe())
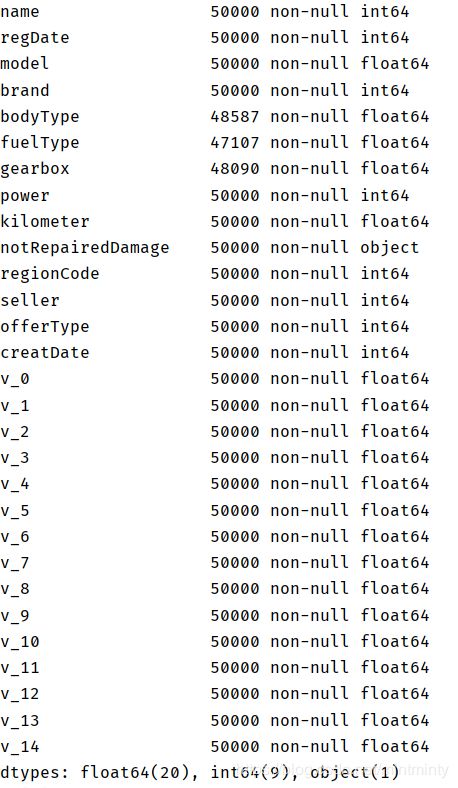
1.3.3 info()熟悉数据类型
print(Train_data.info())
print(Test_data.info())
2. 判断缺失和异常
2.1 缺失值
-
pandas之排序函数sort_values(),功能上类似SQL中的order by
参数 说明 by 指定列名(axis=0或’index’)或索引值(axis=1或’columns’) axis 若axis=0或’index’,则按照指定列中数据大小排序;若axis=1或’columns’,则按照指定索引中 数据大小排序。默认axis=0 ascending 是否按升序排列,默认True:升序排列 inplace 是否用排序后的数据集代替原来的数据,默认False:不替换 na_position {‘first’,‘last’},设定缺失值的显示位置 -
通过.value_counts()显示值的分布情况,结果中 “-” 为空缺值,因为很多模型对nan有直接处理,故我们在此处先不处理,只替换为nan
# 查看每列存在nan情况,并可视化
missing = Train_data.isnull().sum()
Test_data.isnull().sum()
missing = missing[missing>0]
missing.sort_values(inplace=True)
fig_missing = missing.plot.bar()
# 可视化缺省值
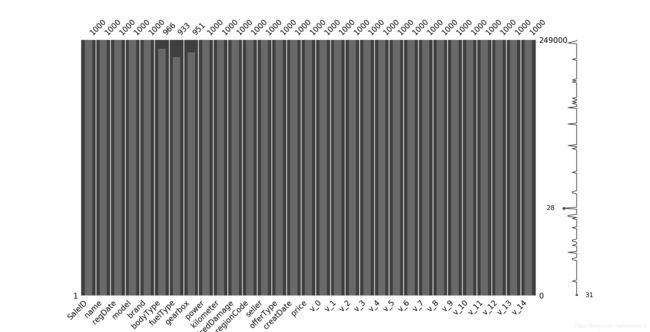
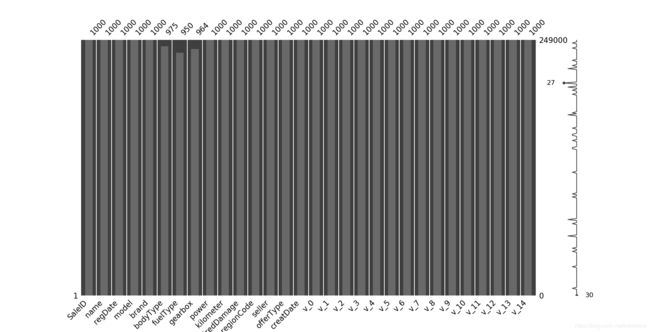
msno.matrix(Train_data.sample(250))
msno.bar(Train_data.sample(1000))
msno.matrix(Test_data.sample(250))
msno.bar(Test_data.sample(1000))
Train_data['notRepairedDamage'].value_counts()
Train_data['notRepairedDamage'].replace('-', np.nan, inplace=True)
# print('训练集缺失值:', Train_data.isnull().sum())
Test_data['notRepairedDamage'].value_counts()
Test_data['notRepairedDamage'].replace('-', np.nan, inplace=True)
2.2 异常值
seller和offerType类别特征严重倾斜,一般不会对预测有什么帮助,故先删除
# print('seller分布:', Train_data['seller'].value_counts())
# print('offerType分布:', Train_data['offerType'].value_counts())
del Train_data['seller']
del Train_data['offerType']
del Test_data["seller"]
del Test_data["offerType"]
3. 了解预测值分布
3.1 总体分布概况
3.1.1 为什么要转化为正态分布
数据整体服从正态分布,那样本均值和方差则相互独立,正态分布具有很多好的性质,很多模型假设数据服从正态分布。例如线性回归(linear regression),它假设误差服从正态分布,从而每个样本点出现的概率就可以表示为正态分布形式,将多个样本点连乘再取对数,就是所有训练集样本出现的条件概率,最大化该条件概率就是LR最终求解的问题。这里这个条件概率的最终表达式的形式就是我们熟悉的误差平方和。总之, ML中很多model都假设数据或参数服从正态分布。
3.1.2 样本不服从正态分布怎么办
- 线性变化z-scores
- 使用Boxcox 变换
- 使用 yeo-johnson 变换
注:盲目假设变量服从正态分布可能导致不准确的结果,要结合分析。例如:不能假设股票价格服从正态分布,因为价格不能为负,故我们可以将股票价格假设为服从对数正态分布,以确保其值≥0;而股票收益可能是负数,因此收益可以假设服从正态分布
3.1.3 和无界约翰逊分布有什么关系
参考文献【2】中指出:当样本数据表明质量特征的分布为非正态时,应用基于正态分布的方法会作出不正确的判决。约翰逊分布族即为经约翰变换后服从正态分布的随机变量的概率分布,约翰逊分布体系建立了三族分布,分别为有界 S B S_B SB、对数正态 S L S_L SL和无界 S U S_U SU
3.1.4 本文中的变换
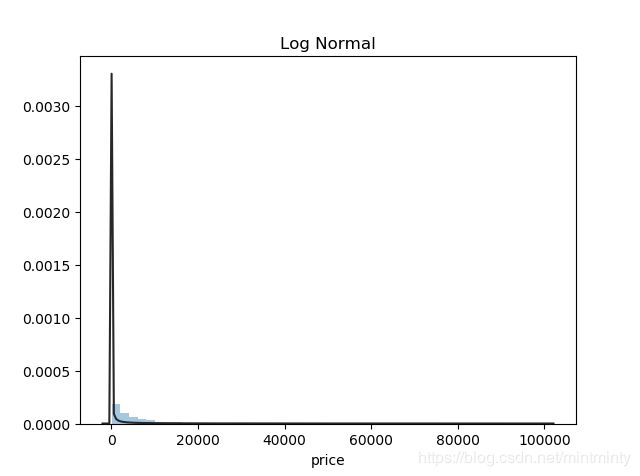
本文分别采用无界约翰逊分布Johnson SU、正态分布normal、对数正态分布lognormal,综合来看无界约翰逊分布对price的拟合效果更好。
y = Train_data['price']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
plt.figure(3); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)
3.2 查看偏度(Skewness)和峰度(Kurtosis)
| 名称 | 定义 | 与正态分布关系 |
|---|---|---|
| 偏度(Skewness) | 衡量随机变量概率分布的不对称性,是相对于平均值不对称程度的度量,通过对偏度系数的测量,我们能够判定数据分布的不对称程度以及方向 | 正态分布偏度为0,即数据分布是对称的。若偏度>0,则分布右偏,分布长尾在右。偏度绝对值越大,说明分布的偏移程度越严重(注:左偏/右偏指的是数值拖尾方向,不是峰位置) |
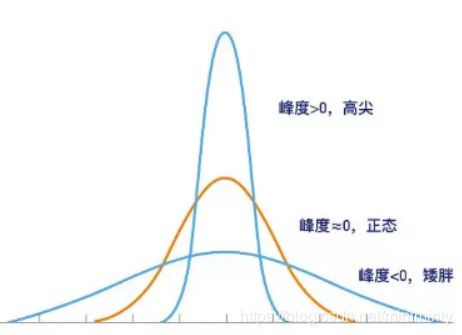
| 峰度(Kurtosis) | 研究数据分布陡峭或平滑的统计量,通过对峰度系数的测量,我们能够判定数据相对于正态分布而言是更陡峭/平缓 | 若峰度=0,分布的峰态服从正态分布;若峰度>0,分布的峰态陡峭(高尖); 若峰度<0,分布的峰态平缓(矮胖) |
sns.distplot(Train_data['price'])
print("Skewness: %f" % Train_data['price'].skew())
print("Kurtosis: %f" % Train_data['price'].kurt())
sns.distplot(Train_data.skew(),color='blue',axlabel ='Skewness')
sns.distplot(Train_data.kurt(),color='orange',axlabel ='Kurtness')
3.3 查看预测值频数
- 大于20000的值很少,其实该处可将其当作异常值处理填充或删除
- 本文中经过log变换之后,分布较均匀,可据此进行预测,这也是预测问题常用的技巧
plt.hist(Train_data['price'], orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()
plt.hist(np.log(Train_data['price']), orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()
4. 特征分析
现状: ‘seller’和‘offerType’已被删除,其他特征均经过了label coding
| Field | Description | 特征属性 |
|---|---|---|
| name | 汽车交易名称,已脱敏 | 类别 |
| regDate | 汽车注册日期 | 数字 |
| model | 车型编码 | 类别 |
| brand | 汽车品牌 | 类别 |
| bodyType | 车身类型 | 类别 |
| fuelType | 燃油类型 | 类别 |
| gearbox | 变速箱 | 类别 |
| power | 发动机功率 | 数字 |
| kilometer | 汽车已行驶公里 | 数字 |
| notRepairedDamage | 汽车有尚未修复的损坏 | 类别 |
| regionCode | 地区编码 | 类别 |
| v系列特征 | 匿名特征,包含v0-14在内15个匿名特征 | 数字 |
若需要处理的数据未label coding,则可通过如下代码对特征进行区分:
# 数字特征
numeric_features = Train_data.select_dtypes(include=[np.number])
numeric_features.columns
# 类型特征
categorical_features = Train_data.select_dtypes(include=[np.object])
categorical_features.columns
本文数据已经label coding,故采用人工区分方法:
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode']
4.1 数字特征
总览
numeric_features.append('price')
print(numeric_features)
4.1.1 相关性分析
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending=False),'\n')
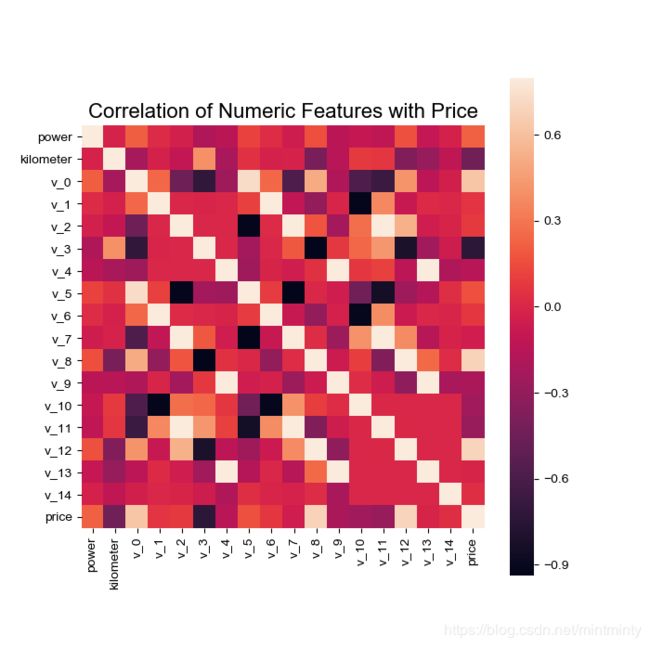
f, ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True, vmax=0.8)
del price_numeric['price']
4.1.2 查看特征偏度和峰值
for col in numeric_features:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(Train_data[col].skew()) ,
' ' ,
'Kurtosis: {:06.2f}'.format(Train_data[col].kurt())
)
4.1.3 每个数字特征的分布可视化
- pd.melt():处理数据,透视表格,可将宽数据转化为长数据,以便于后续分析。形成的数据即为,键:各特征名称,值:特征对应的值
- sns.FacetGrid() :先sns.FacetGrid()画出轮廓,再map()填充内容
f = pd.melt(Train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")
4.1.4 匿名特征分布情况
sns.pairplot():展示变量两两之间的关系(线性或非线性,有无较为明显的相关关系)
- 对角线:各个属性的直方图,用diag_kind属性控制图类型,可选"scatter"与"reg"
- 非对角线:两个不同属性之间的相关图,用kind属性控制图类型,可选"scatter"与"reg"
- hue :针对某一字段进行分类
sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()
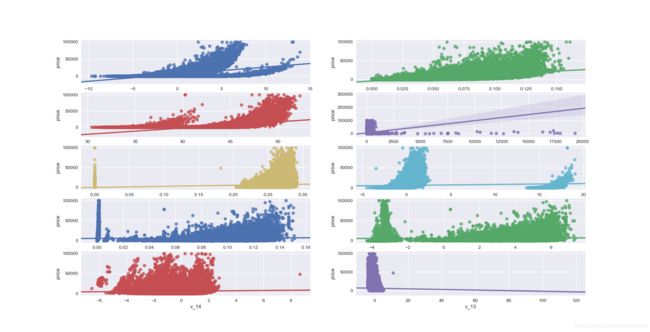
4.1.5 多变量与price的回归关系
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
# ['v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)
v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)
v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)
v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)
v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)
4.2 类别特征
4.2.1 查看nunique分布
for cat_fea in categorical_features:
print(cat_fea + '特征分布如下:')
print('{}特征有{}个不同的值'.format(cat_fea, Train_data[cat_fea].nunique()))
print(Train_data[cat_fea].value_counts())
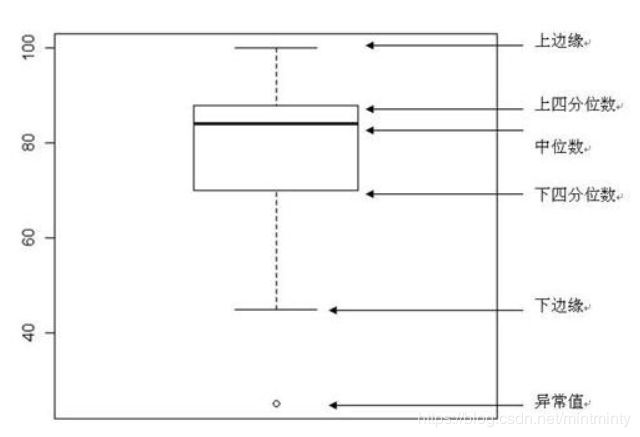
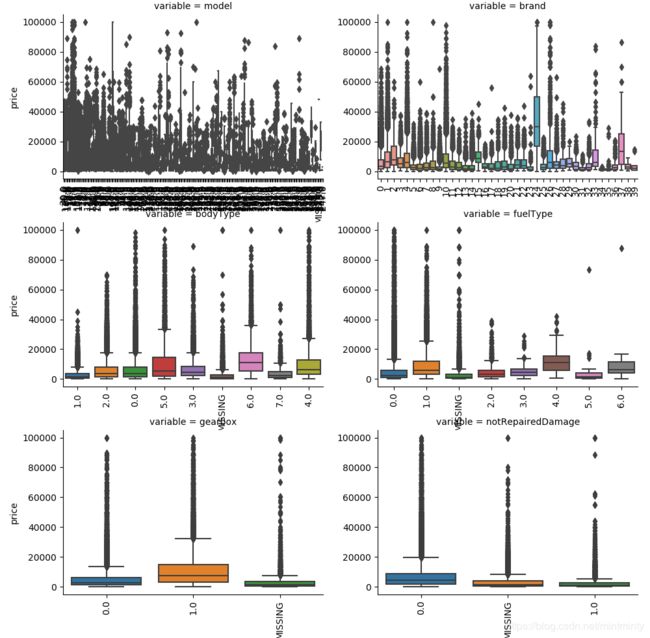
4.2.2 查看箱型图
categorical_features =['model','brand','bodyType','fuelType','gearbox','notRepairedDamage']
for c in categorical_features:
Train_data[c] = Train_data[c].astype('category')
if Train_data[c].isnull().any():
Train_data[c] = Train_data[c].cat.add_categories(['MISSING'])
Train_data[c] = Train_data[c].fillna('MISSING')
def boxplot(x, y, **kwargs):
sns.boxplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(boxplot, "value", "price")
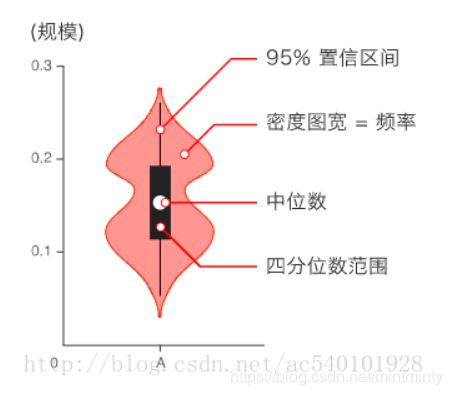
4.2.3 查看小提琴图
4.2.4 查看柱形图
def bar_plot(x, y, **kwargs):
sns.barplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(bar_plot, "value", "price")
4.2.5 类别频数可视化
def count_plot(x, **kwargs):
sns.countplot(x=x)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(count_plot, "value")
5. 生成数据报告
用pandas_profiling生成一个较为全面的可视化和数据报告(较为简单、方便) 最终打开html文件即可
import pandas_profiling
pfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")
6. 收获及未来工作
6.1 收获
- 之前做课题时,数据观察得很粗糙,不…其实是没有什么观察,急匆匆地清洗、分数据集和放模型。经过本节task,了解/使用了多种未曾用过的图,原来可以从那么多的角度、通过那么多方式去了解及展示数据分布,从而为后续工作做好铺垫
- 我实在是太小白了,基础的内容都没有很好掌握。例如在本节中我不理解约翰逊分布是什么、做什么的、为什么要这么做,百度约翰逊分布时,相关介绍也寥寥,尤其百度的结果居然多是某知名女星,…,好气。不过,最后经过一些些努力,我似乎大概搞明白了一点点它的前生今世,但本人统计学相关知识十分薄弱,不能确认我梳理出的内容是否正确,只有错误,烦请指教!
6.2 未来工作
- 后半段可视化的内容,要多加练习,尤其需要不断熟悉代码。除此之外,还要再深入思考(1)现有的分析图是不是都有存在的必要;(2)如何进一步去分析图的隐含信息;(3)对于一个字段/数据的处理上,如何做才能更加准确/有价值的表现信息;(4)以及还有哪些类型的图是可以被利用的,等等。学习是个不断渐进的过程嘛,慢慢消化,多次重复,逐渐创造。
- 李航老师的《统计学习方法》是时候看起来了,欠的债果然是要还的…
- 注:类别特征部分的可视化图,之后会补齐,电脑卡死了 一直不出图。
最后,尤其感谢Datawhale提供的无敌详细的教程!
Datawhale 零基础入门数据挖掘-Task2 数据分析
参考文献/链接
【1】构建模型时为什么要尽量将偏态数据转换为正态分布数据?
【2】张维铭,施雪忠,楼龙翔.非正态数据变换为正态数据的方法[J].浙江工程学院学报,2000(03):56-59.
【3】偏度与峰度的正态性分布判断
【4】数据的偏度和峰度——df.skew()、df.kurt()
【5】Melt函数处理数据,透视表格,宽数据变成长数据
【6】seaborn可视化之FacetGrid()
【7】Seaborn5分钟入门(七)——pairplot
【8】箱型图和小提琴图分析