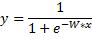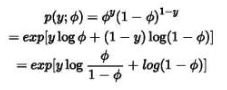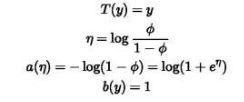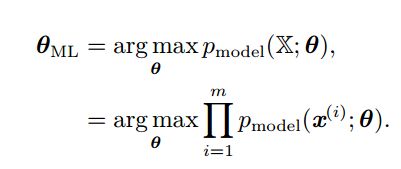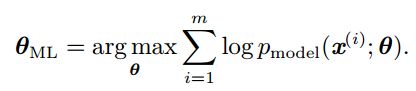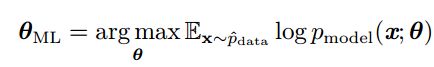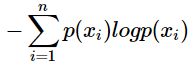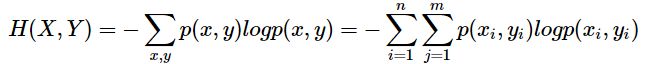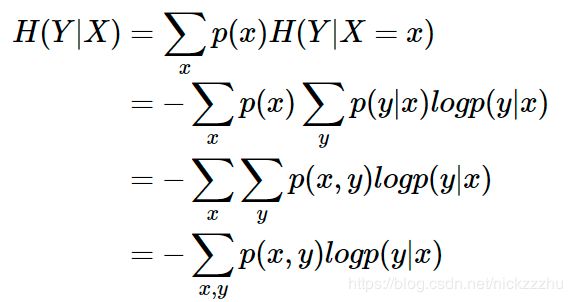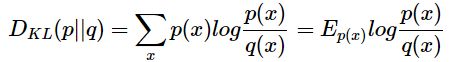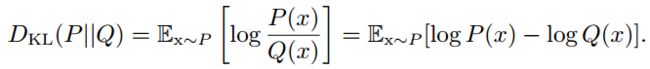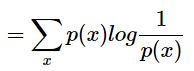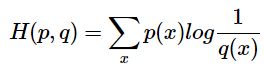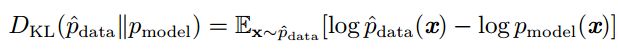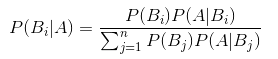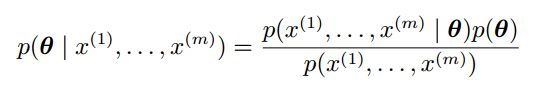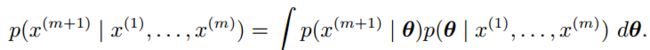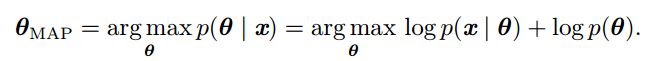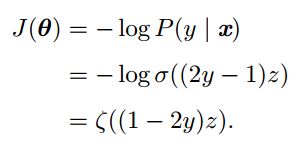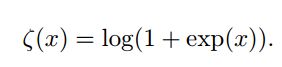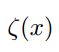逻辑回归与机器学习原理深度总结

动笔写这篇原理深度总结是因为拜读了July大神的支持向量机通俗导论，当时花了一下午时间细细读完觉得豁然开朗觉得SVM不再神秘，并顺手把那篇文章存成了PDF以便日后复习。我觉得那是一篇好文章，因为它非常系统化地总结了SVM，非常深入地介绍了数学细节以满足我这种喜欢寻根问底了解原理的人。

网上讲机器学习的文章很多，但深入讲原理的很少，系统地将机器学习和统计知识结合起来的更少。大部分人（包括我）入门机器学习都是从逻辑回归和线性回归开始，因此本文试图以逻辑回归为起点，将各机器学习的知识点串在一起。文中说的主题都是我在学逻辑回归时思考的问题，以及为了解决这些问题看各种书（比如《深度学习》）、博客、视频（比如吴恩达2008版的斯坦福公开课机器学习）总结而来的。

我们知道，机器学习有监督算法组成的三个部分：假设空间，损失函数，优化过程。所有算法无非是先假设输入X和Y之间存在某种形式的关系，我们要用这个关系来根据X预测Y。既然要预测，就要有评判预测得好坏的标准，就是损失函数。而学习的过程就是用优化过程不断去更新参数，让我们在这个评判标准（损失函数）上表现越来越好。这篇文章就是从三个角度：逻辑回归的假设空间，损失函数和优化过程来总结有监督机器学习的原理

逻辑回归的假设形式大家都非常熟悉，即sigmoid函数：

y是预测类别的概率，或者换一种说法，我们用线性模型来对类别的比率的log函数进行建模：

逻辑回归的损失函数是通过最大似然估计法得到的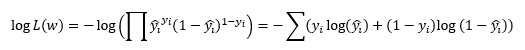：，这里y是真实标签，y_hat是根据逻辑回归公式预测出来的概率值。这个损失叫做交叉熵损失

优化方法一般用梯度下降，其实对大部分参数化的监督的问题，都是用梯度下降方法来寻找最佳参数的。

一，为什么逻辑回归是sigmoid函数，为什么预测的是概率

要引入的概念一：指数族分布

指数族分布（exponential family distribution）的定义是若某概率分布满足以下形式就是指数族分布：

其中η是自然参数，T(y)是充分统计量，exp(-a(η))起到归一化作用。基本上我们熟悉的概率分布密度函数都能写成指数族分布的形式（也就是他们都是指数族分布）。比如伯努利分布：

其中

而把上面η的等式变形一下就是。这里ϕ就是y=1的概率，可以看到这就是sigmoid函数的形式。在此我们先记下这一点。

要引入的概念二：广义线性模型

我们想通过变量X预测Y，因此做出了以下三个假设：

1，p(y|x;θ)服从指数分布

2，一般情况下，T(y)=y，我们的目标是给定x预测T(y)在x下的期望，因此也就是预测E[y|x]

3，参数η和输入x是线性相关的，η=

在这三个假设下推导出的算法成为广义线性模型。

回到逻辑回归的形式

有了以上铺垫，下面来看二分类问题。已知一些x，要预测y，y有2类，取值为0或1.那么很自然地我们就假设y服从伯努利分布，因此y的概率密度函数为，其中ϕ是y=1的概率参数。

而我们想要得到的已知X的条件期望E[y|x]=ϕ==

以上第一个等号是根据伯努利分布的性质，期望=y为1的概率参数；第二个等号根据伯努利分布属于指数分布族的推到，第三个等号根据以上假设3.

由上可见，逻辑回归的假设形式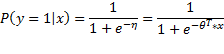是在假设y服从伯努利分布和广义线性模型下推导而来的，逻辑回归属于广义线性模型。

二，为什么是交叉熵损失

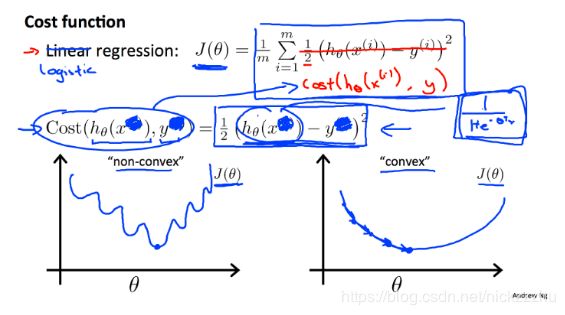
解决了函数形式的疑惑，下面的问题是：为什么做分类的时候就要用逻辑回归的交叉熵损失，不能用线性回归么？大家喜欢逻辑回归，因为它够简单够直接，但线性回归甚至更简单，连sigmoid函数都没有。有人说线性回归的值域是负无穷到正无穷啊你做分类预测概率必须在0-1之间。但“逻辑回归输出概率”是我们的设定，假设抛开概率这个概念直接简单粗暴地设个阈值，比如线性回归的值>0就预测成正类，<0就预测称负类呢？

不能这么做是因为上述方法的损失函数是无法有效优化的，假设这么做我们就无法设计优化过程来学习了

如果我们使用线性回归，并做阈值切断进行分类，假设大于某一值是1否则是-1，这样的算法的损失函数叫0-1损失，借用一下台大林轩田老师的PPT来表述：

这个损失函数是不连续的，优化它是NP HARD问题。因此如果我们执意使用线性回归并用0-1损失来做分类问题，是没有办法设计一个优化过程来求解参数w，也就没有办法进行学习过程。

那还用线性回归的模型形式，y=-1或+1，不用0-1损失，该用平方损失可以么？平方损失损失是个凸函数，很好优化。

要记住，损失函数设计的原则是尽可能准确地表述损失，任务做得好损失函数的值要小，做得差损失函数值要大，这样我们在优化损失函数时才是往正确的方向去的

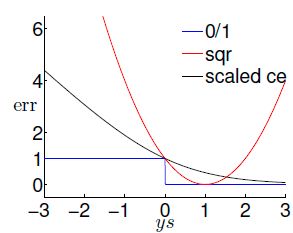
下图直观对比了0-1损失，交叉熵损失，平方损失损失随着y*wx增大的变化

sqr就是平方损失，可以看到其并没有很好地反映wx预测y的准确度。如果y的真实值是-1而s=wx很小，说明预测得准确，我们是希望损失函数很小的。但是此时ys将会是很大的正值，从图像上也可以看出MSE的损失会很大，所以损失函数不能很好地表现预测值和真实值的差距。

那如果用逻辑回归的假设形式，但是损失函数还是用平方损失呢？

借用Andrew Ng的PPT：

是非凸函数如上图左边所示，这导致无法使用梯度下降，因为很容易就陷入局部最优点，无法优化。

再来看我们选定的损失函数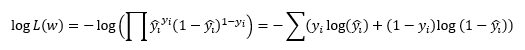。这个损失函数其实是最大似然估计的产物，我们要最小化的损失函数是负对数似然。可以证明这是个凸函数，并且它也很好地反映了预测是准确还是不准。假设y=1，上面留下的就是-log(y_hat)，此时y_hat越大函数值越小。若y=0，上面留下-log(1-y_hat)，y_hat越小函数值越小。所以损失函数会逼着预测值往真实值靠近。

由以上我们可以看到，我们选择逻辑回归，选择交叉熵来做分类问题是有道理的。线性回归虽然简单诱人，MSE虽然直观好记，但并不适用分类情形下解决问题。但是关于损失函数我还有个问题：我们根据最大似然估计法则得到逻辑回归损失函数的公式，可是为什么又叫它交叉熵损失呢？这个公式和熵有怎样的联系？

三，最大似然得到的损失函数和“熵”之间的关系

1，最大似然估计

首先来回顾一下最大似然估计的推导过程

考虑一组有m个样本的数据集X，假设各x独立地由未知的真实数据分布生成。同时再假设我们用参数化的模型得到一族分布。我们想用这个模型分布来估计真实概率分布，而得到模型分布就相当于是得到。的最大似然估计被定义为：

思想是寻找参数使现在发生的x的发生的概率最大。为简化连乘的形式（不好处理且容易数值上不稳定），等价优化log的最大似然估计即log-likelyhood

由于重新缩放代价函数时argmax不会改变，可以将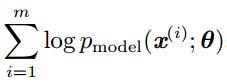除以m得到和训练数据经验分布相关的期望作为代价函数：

这里的符号太多，说得也很绕，再梳理一下就是：是数据真实分布，我们不可能知道；我们只能看到数据的经验分布，我们要做的是寻找参数，使得参数确定的模型分布可以尽量和观察到的经验分布相近，从数学上表述就是找到让最大，写成公式就是

以上就是最大似然估计和熵产生关系的地方。在继续推导前，先回顾一下各种熵的概念。

“熵”最初来源于热力学，后来被香农引入信息论有了“信息熵”。机器学习融合了信息论、统计学、计算机科学等多门学科，所以在机器学习中也经常能看到“熵”这个字眼：信息熵、条件熵、相对熵、交叉熵等等。各种熵的概念错综复杂，如果抓个工业界的，除非是为了应付面试零时抱佛脚的人，其他人很难立刻给一个清晰的解释。但这里毕竟是在说理论，在说到逻辑回归和熵的关系前还是要先把各种熵说清楚

2，信息熵

熵在信息论中是度量不确定性的。假设有随机事件集合X={x1,x2,...,xn}，其中xi发生的概率是p(xi)，则xi的自信息是

I(xi)=-log(p(xi))

而对于整个集合X，其信息熵是对自信息的期望E(I(X))=

以上是对单变量随机事件。熵的公式也可以很容易扩充到二变量或多变量的情况，比如二变量的信息熵是

3，条件熵

假设有两个（非独立的）随机变量X,Y，已知X的情况下，度量Y的不确定性的就是条件熵，它是给定X条件下Y的条件概率分布的熵对X的数学期望

数学上可以证明，条件熵=联合的熵-单独的熵： H(Y|X) = H(X,Y)-H(X)

直观上也比较好理解：两个随机事件X,Y放在一起的不确定性减去其中一个随机事件X的不确定性等于在知道了X的情况下随机事件Y的不确定性。

4，相对熵（KL散度-Kullback-Leibler Divergence）

既然名字中有“相对”两字，说明它和度量两者之间的关系有关。其实相对熵，也叫KL散度，是度量两个概率分布之间差异的。假设对于随机变量X有两种分布p(x)和q(x)，则这两个分布的相对熵是：

上面这个公式中，KL散度是概率分布p,q的对数差在概率分布p上的期望值：

很显然，如果p=q，他们的比值=1，log值=0，则相对熵=0

数学上还可以证明，KL散度>=0

需要注意的是，尽管KL散度衡量了两个分布的差异，但却不能看成“距离”，因为它是不对称的。选择Dkl(p||q)和Dkl(q||p)会得到完全不同的结果。比如下面这个图中，p是两个高斯分布混合，q是单个高斯分布，用不同方向的kl散度选择最接近p的q得到了完全不同的高斯分布：

5，交叉熵

现在有关于样本集的两个概率分布p和q，p是真实分布。真实分布的不确定性也就是信息熵是

如果用非真是分布q来衡量真是分布p的不确定性，得到的就是交叉熵

上面还说过相对熵，或者叫KL散度的公式是

所以很明显，交叉熵、相对熵KL散度和信息熵的关系是

6，最大似然估计、交叉熵和KL散度

回顾最大似然估计的目标函数，要找到使最大，换句话说就是要使最小

假设分布和分别是真实分布（上文的p）和假设的分布（上文的q），则这两个分布间的差异用KL散度衡量：

可见KL散度和最大似然估计的目标间差了左边那一项，而左边项只涉及到数据生成过程和模型参数无关，所以要最小化两个分布之间的差异就是最小化右边那一项。同时再根据交叉熵和KL散度的关系：

，可见KL散度就是交叉熵减去p的信息熵，即，而这一项刚刚已经说过和参数是无关的。所以最大似然其实就是最小化KL散度，从物理上理解，KL散度是衡量两个分布间的差异的，最小化它就是最小化模型假设和观测数据分布的差异。同时最小化KL散度实质上就是最小化分布之间的交叉熵。其实交叉熵损失函数是应用于分类问题的损失函数，不局限于逻辑回归，这里只是借着逻辑回归这一基础算法把分类问题损失函数的原理弄清楚了

四，最大似然估计、贝叶斯统计推断、最大后验概率和正则化

前面我们进行了深入讨论的最大似然估计都是频率派统计的方法，这里要提到另一个统计学派：贝叶斯派

贝叶斯派统计思想和频率派完全不同，并且我发现一般的数学教育对其提及很少。比如我作为计算机专业的学生，完全不记得大学学统计的时候有教过贝叶斯的思想。顶多记得一个贝叶斯公式：

这是个非常著名和有用的公式，比如朴素贝叶斯模型就是利用这个公式，可以对某些问题（如垃圾邮件分类）有很好的解决。贝叶斯统计的思想是：概率反映了知识确定的程度，我们对每件事都有自己的先验概率（可以将其理解成自己的主观猜想，这个先验不一定正确），在观测了数据后我们会通过数据结果修正先验，得到后验概率。也就是

P(Y|X) = P(X|Y)*P(Y)

应用到参数估计上来，频率估计的观点是真实参数是确定的，可惜我们不知道，因此我们根据观测到的数据设计一个数据到参数的映射即统计量，以此来进行对参数的点估计。贝叶斯的观点是参数不是确定的，而是否从某个分布的随机变量。我们在观测数据前猜测服从某分布（先验），然后通过观测到的数据（似然）修正我们的只是，得到的后验概率，也就是我们对数据新的信念

此时可能会说，我又不知道参数分布是什么样的，我怎么猜一个先验分布呢？确实，正是由于我们一开始不知道参数什么样，所以通常先验选一个“最不确定”的分布。上面已经知道，最不确定就是信息量最大，也就是熵最高。均匀分布和高斯分布均是高熵的分布，因此经常用于先验。这也解释了为啥我们上来就说“假设XX服从高斯分布”，因为我们本来不知道它服从什么分布，只能选一个最不确定的先假设上去

那么先验在我们估计参数的时候的用处在哪呢？它会让概率质量、密度朝着参数空间中偏向先验的方向便宜，这和正则化有异曲同工之处。试想比如L2正则化，不正是我们人为地限制各参数的大小，期望他们的绝对值在0周围么。在最大后验估计中还会提到先验和正则化的关系

回到贝叶斯估计，它在预测的时候不像最大似然，使用的点估计，而是使用的全分布。假设观测了m个样本后，要预测第m+1个样本时

贝叶斯估计中就是个随机变量，每个有正概率密度的都会对预测Xm+1有贡献，其贡献由后验概率密度加权。

原则上，如果使用贝叶斯统计，我们应该用参数的完整贝叶斯后验概率分布进行预测。但对大多数有意义的模型而言，贝叶斯后验概率的计算很难做，而点估计提供了一个可行的近似解。利用最大后验估计MAP，可以用先验来加入我们的看法影响模型，同时又用最大似然法则利用数据修正先验。最大后验估计选择后验概率最大的点作为参数的点估计：

上面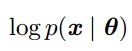对应标准的对数似然，对应先验概率。由于我们对先验没有任何知识，假设其服从高斯分布，这是一个均值为0，方差为的高斯分布。将高斯分布概率密度公式带入上述最大似然公式，可以得到的结果是和一个与参数无关也不会影响学习过程的数。所以可以看到，具有高斯先验权重的MAP贝叶斯推断等价于加了权重衰减的最大似然估计。MAP，也就是L2正则化，增加了无法从训练数据中获取的先验信息，减少了单纯最大似然估计的方差，但是增加了偏差。事实上，许多正则化方法都可以被解释为贝叶斯推断的MAP近似。

五，sigmoid单元，神经网络和梯度下降法

先回顾一下梯度下降法：

在梯度下降法中，给定参数w，希望寻找一个新的w使得损失函数f变小，并且希望在更新w时可以让f减小得最快，即寻找一个f下降最快的方向，该方向是梯度方向的反方向（梯度=J对所有w求偏导的向量导数）。梯度下降建议新的点为

 

我们知道，逻辑回归其实就是单层单节点的神经网络，早期的神经网络就是多个sigmoid激活单元堆叠在一起。为什么现在激活函数换成了ReLU呢？为什么都说隐藏层使用sigmoid效果不好呢？但为什么输出层还是可以使用sigmoid呢？

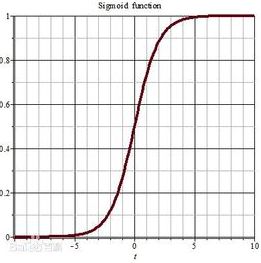
原因和梯度下降有关。梯度下降的要发挥作用，重要的一点是进行偏导数的点梯度不能为0，否则梯度消失了，参数就无法更新（当然梯度也不能爆炸，但是sigmoid函数没有梯度爆炸问题）。来看一下sigmoid函数的形状：

可以看到在大部分区间这个函数都是饱和的，梯度为0.如果在隐藏层中使用sigmoid函数，则大部分情况下都不能有效更新参数。反之使用ReLU的话，既可以引入非线性，同时梯度=1，参数可以更新。

而对于输出层，再来回顾最大似然估计的损失函数：

如果y_hat是由sigmoid得到的，则exp正好可以和log抵消。我们使用最大似然估计来学习一个由sigmoid参数化的伯努利分布，损失函数为

其中

 

称为softplus函数，其图像为：

可以看到，损失函数只有在(1-2y)z取绝对值非常大的负值时才会饱和，而这时模型已经得到了正确答案：此时y=1且z=非常大的正值，或y=0且z=非常大的负值。而在错误的地方，softplus函数不会饱和，因此在错误的时候，可以很快基于梯度改正z，也就是更新参数。

六，后记

这篇文章主要的知识来源是有AI圣经之称的《深度学习》和Andrew Ng的2008版斯坦福公开课机器学习，同时还借鉴了各种博客的文章、知乎的回答（我学习机器学习以来浏览各种信息，看到有用的知识点就零散地记下来）。写总结的目的是为了整理自己的知识体系，同时对知识有系统化的记录。机器学习实践非常重要，但理论是帮助我们更好实践的基础，我一直认为只有深入了解模型原理，才能使用的时候得心应手。我自己还一直处于学习状态，若有读者或大神发现文章总结中有错误之处，请不吝批评指正。