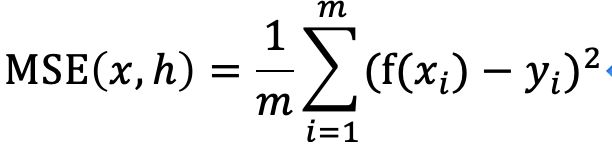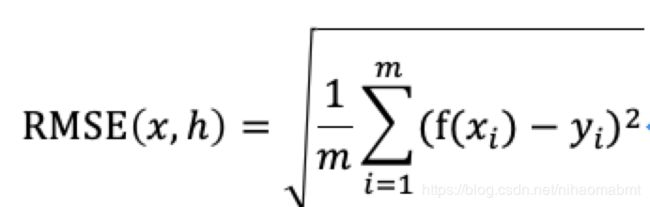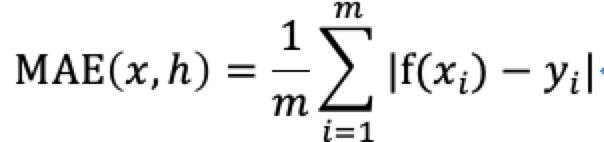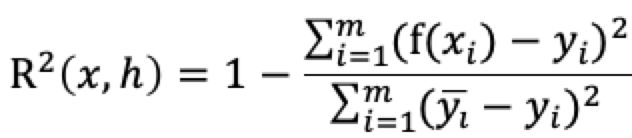机器学习入门研究（四）-评价指标-回归和聚类

目录

一、回归

1.均方误差MSE

2.均方根误差(RMSE)

3.平均绝对误差MAE

4.确定性系数R2

二、聚类

1.ARI

2.轮廓系数

三、总结

---

上一篇机器学习入门研究（三）-评价指标-自我感觉总结的还不错的介绍了关于分类模型中的评价指标，这篇主要介绍回归和聚类模型中的评价指标。

一、回归

1.均方误差MSE

Mean Squared Error，也称为L2损失，表示预测值（通过模型计算得到的值）和实际值在y轴上的距离差的平方的平均值。

其中f(x)为该回归模型。

这个是线性回归中常用的损失函数。该值越小，说明该线性模型越好，具有更好的精确度。更能体现的是数据的变化程度。

对应的Python中的函数为

sklearn.metrics.mean_squared_error(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)

对应的参数如下：

参数	含义
y_true	实际样本数据
y_pred	预测样本数据
sample_weight	样本权重，n为矩阵，n为样本类别
multioutput	多维输出，默认为uniform_average，表示计算所有元素的均方误差，返回一个单独的数值； raw_values:计算对应列的均方误差，此时对应的y_true和y_pred都是多维数组。返回的是一个与列数相等的一维数组； [x,y..]也可以是一个对应列数的一维数组，raw_values返回对应列的均方误差与该一维数组对应位置的乘积之和，也就是raw_values返回的一维数组的每个元素的比例关系，返回的是一个单独的数值

2.均方根误差(RMSE)

Root Mean Squared Error，又称为标准误差，表示的是均方误差的算术平方根。此时该误差值和样本数据是一个数量级，可以更好的藐视数据。

该值说明样本的离散程度，在非线性拟合中，该值越小越好。

在Python中没有特别的函数，通常采用下面方式获得

np.sqrt(mean_squared_error(y_true,y_pred))

3.平均绝对误差MAE

Mean Absolute Error，也称为F1损失。表示的是预测值（通过模型计算得到的）和实际值在y轴上的距离的绝对误差的平均值。能够更好的反映预测误差的实际情况。

对应的Python函数为： 

sklearn.metrics.mean_absolute_error(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)

参数同mean_squared_error

4.确定性系数R2

Coefficient of Determination。

在该公式中，分子就是预测值和实际值的误差的平方之和，而分母就是实际值的平均值与实际值的误差的平方之和。R2取值介于0～1之间，越接近1，说明该模型的效果越好。

对应的Python函数为： 

sklearn.metrics.r2_score(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)

参数同mean_squared_error 

二、聚类

聚类就是将样本集划分为若干互不相关的子集，即样本簇。聚类的最终目标就是聚类结果的簇内相似度高且簇外相似度低。所以对于聚类的评价指标就分为两大类：一类就是将聚类结果与有标签的样本进行比较，称为外部指标，另一类就是直接考察聚类结果而不利用任何参考模型，称为内部指标。

因为聚类的有些内容现在还有些不太理解，所以简单的先列下大体概念，等着熟悉了之后在回来更新这里的内容。

1.ARI

Adjusted Rand Index，调整兰德指数。用来评价样本数据本身带有正确的类别信息，即外部指标。

对应的Python函数为：

sklearn.metrics.adjusted_rand_score

2.轮廓系数

Silhouette Cofficient，适用于实际样本未知的情况，也就是样本数据中没有所有类别，即内部指标。

取值范围为[-1,1]，同类别样本距离相近且不同类别的距离越远，分数越高。

对应的Python函数为：

sklearn.metrics.silhouette_score

三、总结

以后在后面的学习中再看看怎么去选择合适的衡量指标，也就是这些在实际评估模型中怎么发挥作用。