机器学习入门研究（十六）—K-means

目录

 

无监督学习

无监督学习分类

聚类中的几个实例

K-means算法原理

sklearn中的API

实例

降维

PCA

在sklearn中的API

简单的实例

---

无监督学习

相对于前面学习的各种监督学习的算法，都是既有特征又有目标值的学习；而无监督学习就是没有目标值，只有特征值，要根据这些特征值自行训练，然后在进行分类预测。

无监督学习分类

主要有两类：

聚类：K-means（K均值）、均值漂移聚类、基于密度的聚类方法（DBSCAN）、用高斯混合模型（GMM）的最大期望（EM）聚类、凝聚层次聚类、图团体检测（Graph Community Detection）

降维：PCA

聚类中的几个实例

1.一家广告平台需要跟进相似人口学特征和购买习惯将美国人口分成不同的小组，以使广告客户可以通过有关联的广告接触到他们的目标客户。

2.一家民宿需要将自己的房屋分成不同的社区，以便用户能更轻松的查询这些清单

对于上面的实例怎么进行归纳和分类呢？这就是无监督学习，从无标签的数据开始学习，从而进行归纳和分组。

今天主要总结下K-means算法的原理。

K-means算法原理

K为超参数，K就是我们要分类类别的个数，如果需求有确定分成几类，那么K的取值就是几；那如果K的取值不确定，那么K值就可以通过机器学习入门研究（七）-模型选择与调优对参数进行调优。

下面主要通过图文来描述下K-means的原理：

假设有几个点，要把这些点分成两类，那么简单的举几个例子来解释下这个过程：

此时K的取值就为2

1.随机取2个点，分别标记不同的颜色为粉色和紫色：

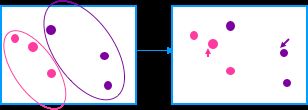
2.然后计算其他点与这两个随机点的距离，然后对比与这两个随机点的距离，离那个点近，就标记成相同的颜色，上述的图就变成了下面的图示：

3.根据两个不同颜色就可以将区域划分成两部分，分别找出这两个区域的中心点。所谓的中心点就是该区域的所有点的均值，此时变成如下图：

4.从上图中的右边图中可以看到计算出来的中心点（箭头指示）和刚开始的随机点（稍微大点）并不是同一个点，所以就需要将计算出来的中心点作为随机点，重复2.和3.，直到计算出来的中心点和随机点为同一个点或者很接近的一个点。

sklearn中的API

在sklearn中提供了API来实现K-means算法。

sklearn.cluster.KMeans(self, n_clusters=8, init='k-means++', n_init=10,
                 max_iter=300, tol=1e-4, precompute_distances='auto',
                 verbose=0, random_state=None, copy_x=True,
                 n_jobs=None, algorithm='auto'):

其中参数如下表：

字段	含义
n_clusters	超参数k，簇个数，也就是分成类别的个数。默认为8，
init	初始簇中心获取方法。默认为'k-means++'：能加速迭代过程中的收敛 还可以有： Random：随机选取 narray向量取值：(n_clusters, n_features) ，并要给到初始质心
n_init	不同的初始簇中心初始化算法的次数。默认为10
max_iter	最大迭代次数
tol	迭代收敛条件
precompute_distances	预计算距离。计算速度更快但是会占用更多内存 默认值为auto。如果样本数x聚类数>12000000，则不预计算距离。大约100MB True：总是预先计算距离 False：永远不预计算距离
verbose	冗长模式
random_state	随机状态
copy_x	是否复制原始值，默认为True：原始数据不会改变；
n_jobs	计算所用的进程数
algorithm	Kmeans的实现算法 auto： full：使用EM方式实现 elkan：

返回的参数：

参数	含义
cluster_centers_	返回向量，[n_clusters, n_features] (聚类中心的坐标)
Labels_	每个点的分类
intertia_	每个点到其簇的质心的距离之和

实例

可以查看机器学习入门研究（十七）— Instacart Market用户分类提供的一个实例。 

降维

降维指的是在某些限定条件下，降低随机变量（特征）个数，得到一组不相关主要量的过程。所以这里的降维指的就是降低特征个数，对于在提供的样本数据是一个二维数组，也就是一个行代表样本个数，列代表特征个数的二维数组，那么也就是减少这个二维数组的列个数。

通常在降低特征的个数的时候，通过就是减少相关特征的个数。那么什么是相关特征呢？

相关特征就是特征之间存在相似性，例如，预测一个地区的相对湿度和降雨量作为特征来预测的时候，那么这个相对湿度和降雨量就是相对特征，这两个特征带来的信息是相似的。

如果相关特征比较多时，说明冗余信息就很多，影响到最后的预测结果。

降维的方法主要有下面两种：

1）特征选择

原有特征中找出主要特征

2）主要成分分析PCA

PCA

PCA可以把可能具有相关性的高维变量合成线性无关的低维变量，称为主成分（ principal components）。新的低维数据集会尽可能的保留原始数据的变量。

PCA就是将高维数据转化成低维数据的过程，在这过程中可能会舍弃原有的数据，创建新的变量。也就是通过损失少量信息的前提下进行数据维数的压缩，尽可能降低原数据的维数，降低复杂度。

PCA的整个计算过程就是通过一个矩阵运算得到主要成分分析的结果

在sklearn中的API

在sklearn中的API如下：

sklearn.decomposition.PCA(self, n_components=None, copy=True, whiten=False,
                 svd_solver='auto', tol=0.0, iterated_power='auto',
                 random_state=None)

其中参数如下：

参数	含义
n_components	小数类型：保留百分之多少 整数：将特征减少到多少
copy	是否复制原始值，默认为True：原始数据不会改变；
whiten	是否将降维后的数据进行归一化。默认为False，一般不需要进行归一化
svd_solver	指定奇异值分解SVD的方法。有四个‘auto’, ‘full’, ‘arpack’, ‘randomized’取值。 ‘auto’,：在下面的三种方法中权衡 ‘full’：传统的SVD。使用scripy库对应实现 ‘arpack’：直接使用scripy的sparse SVD实现，arpack和randomized的适用场景类似，区别是randomized使用的是scikit-learn自己的SVD实现 ‘randomized’：数据量大，数据维度多同时主成分数目比例又比较低

 返回的参数

参数	含义
explained_variance_	降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分
explained_variance_ratio_	降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分

简单的实例

原数据为一个3x4的二维数组，降维之后变成了一个3x3的二维数组。

def pca():

    #1实例化PCA实例
    data = [[2,8,5,1],[9,7,4,2],[5,8,2,7]]
    print("原数据：")
    print(data)
    pca = PCA(n_components=3)
    #2）调用fit_transfa
    data_new = pca.fit_transform(data)
    print("原降维之后的数据：")
    print(data_new)
    return None

运行之后：

原数据：
[[2, 8, 5, 1], [9, 7, 4, 2], [5, 8, 2, 7]]
原降维之后的数据：
[[ 4.26857026e+00 -4.73024706e-01  2.57350359e-16]
 [-1.68373209e+00  3.59761365e+00  2.57350359e-16]
 [-2.58483817e+00 -3.12458895e+00  2.57350359e-16]]