数据结构视频笔记
01 绪论
”让编程改变世界,让我们成功吧!“ -- 小甲鱼
什么是数据结构
- 程序设计 = 数据结构 + 算法
- 关系,数据元素之间的一种或多种特定关系的集合。
逻辑结构和物理结构
逻辑结构:指数据对象中数据元素之间的相互关系。
物理结构:数据逻辑接哦故在计算机中的存储形式。
四大逻辑结构:
- 集合结构:数据元素除了属于同一个集合外没有任何关系。
- 线性结构:数据元素是一对一的关系。
- 树形结构:元素间一对多的层次结构(传销)。
- 图形结构:最复杂,多对多,人与人的认识关系
物理结构:内存的存储方式
- 顺序存储结构:数据元素存在地址连续的存储单元中,数据间的逻辑关系和物理关系一致。
- 链式存储结构:数据元素存放在任意的存储单元里不需要连续。不过需要一个指针存放数据元素的地址,通过地址找到相应的数据元素的位置,每个数据都需要跟多的空间存号码(例子:医院那号排队你需要关注的前一个号)
02 算法
解决特定问题求解步骤的描述。简化解决问题的方法、提高解决问题的速度。
五个基本特征:
- 输入:零个也可以
- 输出:至少一个,输出的形式可以是打印形式,或者放回一个值
- 有穷性:
- 确定性:在一定条件下只有一条执行路径,相同的输入只能有唯一的输出结果
- 可行性:算法每一步都要可行,每一步都能通过执行有限次数完成
算法设计的要求
- 正确性:有五个基本特征,没有语法错误,合法的输入,对于非法输入有说明,对于刁钻的输入值也能有满足要去的结果。
- 可读性:便于阅读、理解和交流。
- 健壮性:对于非法输入有相应的处理方式而不是奔溃。
- 时间效率和存储量低:
03 时间复杂福和空间复杂度
算法效率的度量方法:
- 事后统计方法:设计算法测试程序和数据,利用计算机计时器对不同的算法编制的程序的运行时间进行比较。(需要事先写好算法测试程序花费的时间和精力大)
- 事前分析估算方法:在计算机程序编写前,依据统计方法对算法进行估算。
影响算法效率:
- 算法采用的策略、方案
- 编译产生的代码质量
- 问题的输入规模
- 机器执行指令的速度
分析算法的运行时间时,重要的是把基本操作的数量和输入模式关联起来。
函数的渐近增长:x-y函数图 有什么有关?n的指数、
04 时间复杂度和空间复杂度2
相信你就是你想要成为的那个人
算法时间复杂度:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)是关于问题规模的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。n为输入规模;T(n)=0(f(n)),表示执行时间的增长率和f(n)的增长率相同,称为算法的渐近时间复杂度,简称时间复杂度f(n)是问题规模n的某个函数。执行次数=时间; O():大O记法。
推倒大O阶方法:
- 用常数1取代运行时间中所有的加法常数。
- 在修改后的运行次数函数中,只保留高阶项
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数
- 得到最后结果
05 时间复杂度和空间复杂度3
函数调用的时间复杂度分析:
算法的空间复杂度:
用时间复杂度来指运行时间的需求,空间复杂度指空间需求。
闰年判断算法:
- 逐个判断(节省空间)
- 先做个表记录各个年份是否为闰年(节省时间)
用空间换取时间
06线性表
定义:由零个(空表)或多个数据元素组成的有限序列。排队,线一样的性质结构List:1.有顺序2.只有一个直接前驱元素和直接后继元素3.有限的
数据类型定义:是指一组形之下相同的值得集合及定义在此集合上的一些操作的总称。
抽象数据类型ADT abstract data type:
ADT 抽象数据类型名
Data
数据元素之间逻辑关系的定义
Operation
操作
endADT
07 线性表
让编程改变世界,让梦想创造奇迹。
抽象数据类型:把数据类型和相关操作捆绑在一起。
Operation:
- InitList(*L):初始化操作,建立一个空的线性表L。
- ListEmpty(L):判断线性表是否为空表,返回true false;
- ClearList(*L):将线性表清空;
- GetElem(L,i,*e):将线性表L中的第i个位置元素值返回给e。
- LocateElem(L,e):在线性表L中查找与给定值e相等的元素,如果查找成功返回该元素在表中的序号,否则返回0表示失败;
- ListInsert(*L,i,e):在线性表L中第i个位置插入新元素e;
- ListDelete(*L,i,*e):删除线性表L中第i个位置元素,并用e返回其值;
- ListLength(L):返回线性表L的元素个数;
08 线性表 09 线性表
线性表的物理存储结构:
顺序存储结构:封装需要三个属性:1. 数据data存储空间的起始位置。2. 线性表的最大存储容量MaxSize。 3. 线性表当前长度:length。 地址计算方法:LOC(ai) = LOC(a1) + (i-1)*c T(n)=O(1). *获取元素的操作:GETElem 插入操作****删除操作
优点:
- 无须为表示表中的元素之间的逻辑关系而增加额外的存储空间。
- 可以快速存取表中任意位置的元素
缺点:
- 插入和删除操作需要移动大量元素
- 当线性表长度变化较大时,难以确定存储空间的容量
- 容易造成存储空间的“碎片”
链式存储结构:
特点:用一组任意的存储单元存储线性表的数据元素,这组存储单元可以存在内存中未被占用的任意位置。数据域****指针域:内存储的信息称为指针或链。这两部分信息组成数据元素称为存储映像,也称为结点(Node)
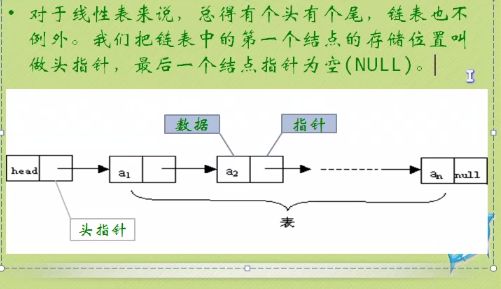
n个结点链接成一个链表,线性表的链式存储结构。因为此链表的每个结点中只包含一个指针域,所以叫单链表
链表:头:头指针 尾:null
10 11 12 13 线性表
头指针:
头指针:是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针。
头指针具有标识作用,所以常用头指针冠以链表的名字(指针变量的名字)
无论链表是否为空,头指针均不为空。
头指针是链表的必要元素。
头结点:
头结点是为了操作的统一和方便而设立的,放在第一个元素的结点之前,期数据域一般无意义(但也可以用来放链表的长度)
有了头结点,对子啊第一元素结点前插入结点和删除第一结点起操作与其它结点的操作就统一了。
头结点不一定是链表的必须要素。
单链表的读取:遍历链表从头结点开始找。时间复杂度: O(n)
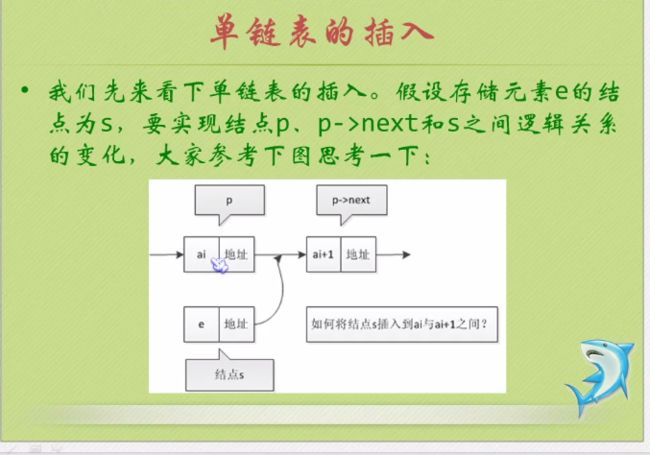
单链表的插入:只需改变地址指向
单链表的删除:
上述的操作都需要先找到元素所处的位置,时间复杂度都为:O(n)
(第一部分遍历查找第i个元素,第二部分就是实现插入或者删除)和顺序比没有优势;
但是,要插入多个就会有差距,因为只找一次i;
单链表的整表创建
创建单链表的过程是一个动态生成链表的过程,从“空表”的初始状态起,依次建立各元素结点并逐个插入链表。
- 头插法建立单链表:把新元素放在表的第一个位置;
- 让新结点指向头节点
- 让表头的next指向新节点
- 尾插法建立单链表:
单链表的整表删除
必须从头开始一个一个删除,将第一个指向第三个,去除中间的,依次下去,直到第一个指向null;
单链表与顺序存储结构的优缺点:
- 存储分配方式:顺序存储结构是用一段连续的存储单元依次存储线性表的数据元素。单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素。
- 时间性能:
- 查找: 顺序:O(1) 单链表:O(n)
- 插入删除:顺序:O(n) 单链表:计算出位置后:O(1)
- 空间性能:顺序存储结构需要预分存储空间,分大了浪费,分小了容易溢出。单链表:不需要提前分配空间,元素个数也不受限制。
14 线性表
静态链表
用数组描述的链表叫做静态链表;
- 对数值的第一个和最后一个元素做特殊处理,他们的date不存放数据。
- 通常把未使用的数组元素称为备用链表
- 数组的第一个元素,即下标为0的元素的cur就存放备用链表的第一个结点的下标
- 数组的最后一个元素,即小标为MAXSIZE-1的cur则存放第一个有数值的元素的下标,相当于单链表中的头结点作用。
1
2
17 线性表
循环链表
绕
单链表:不从头节点出发就不能访问到全部的节点。
循环链表:将单链表中终端结点的指针端由空指针改为指向头结点,使整个单链表形成一个环,单循环链表。
区别:判断空表方法:
- 单链表:head->next是否为null
- 循环链表:head->next是否等于head
18 约瑟夫问题
犹太历史学家Josephus的故事:在罗马人占领乔塔帕特后,38个犹太人与Josephus及他的朋友躲在山洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了自杀的方式,41个人排成一个圆圈,由第一个人开始报数,每报道第3个人该人就必须自杀,然后由下一个重新报数,直到左右人死亡为止。
然而Josephus和他的朋友并不想遵从,于是Josephus将朋友和自己安排在16和31的位置,逃过了这场死亡游戏
编程:利用程序把41个人自杀的顺序编号输出
视频上还有一道题。
19 线性表
循环链表的特点
访问最后一个结点:
- 单链表需要O(n)
- 循环链表需要O(1):对循环链表进行一个小的改变
这时判断链表为空的方法:rear是否等于rear->next
特点:无须增加存储量,仅对链表方式稍作改变,即可使得表处理更加方便灵活。
例题:实现将两个线性表(a1,a2,a3,...an)和(b1,b2,b3,b4...,bn)连接成一个线性表(a1,a2,...an,b1,b2...bn)
分析:
1. 如果是单链表就需要遍历第一个链表找到an,然后把结点b1链到an的后面,时间复杂度是:O(n);
2. 尾指针表示的单循环链表,只需修改指针,无须遍历,O(1)
例题二:判断单链表中是否有环
有环定义:链表的尾节点指向了链表中的某个节点。
判断方法:
- 使用p、q指针,p向前走一次走一步,q向前走每次从头开始走,判断p,q的步数是否相等。
- 快慢指针,p走一步,q走两步,如果q=p则有环