Python入门基础语法101-Wayne1
文章目录
- 0. 计算机硬件基础
- 冯诺依曼体系,梯度下降
- 动态语言和静态语言
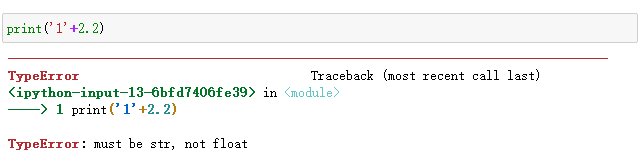
- 隐式类型转换
- Python基础语法
- 数字运算
- 数值类型
- 加减乘除
- 字符串处理
- r和f前缀
- 转义序列
- 续行
- 标识符
- 进制
- 二进制转16进制
- 特殊十六进制记忆
- 二进制转8进制,每3位一断:
- 十六、八进制转二进制
- 十进制转2、8、16进制
- 码制
- 原码
- 反码
- 补码
- 补码求原码
- 补码加、减运算公式
- 运算符
- 比较运算符
- 成员运算符
- 身份运算符
- 位运算
- 逻辑运算真值表
- Python运算符优先级:算数运算>比较>逻辑;not>and>or
- 2. 表达式
- 内置函数
- Type
- isinstance 的用法
- False等价
- Print 的sep和end
- 取整运算
- ceil向上;floor向下;
- // 除, 向下取整
- int只截取整数部分,正数向下取整;负数向上取整
- round 四舍六入五取偶
- 惰性对象range
- 3. 分支和循环
- 分支语句
- 循环语句
- 3. 线性表
- 线性表的类别
- 3.1 Python列表的操作
- 3.2 Python元组的操作: 待撰
- 3.3 Python字典的操作 :待撰
- 3.4 Python集合的操作:待撰
- Python入门测试
0. 计算机硬件基础
基于图灵提出的概念,冯诺依曼体系:计算机包含运算器、控制器、输入设备、输出设备、存储器。其中CPU包含了运算和控制功能,是编程主要针对的对象。CPU不直接在IO设备输入输出数据;IO设备输入输出是有内存操作的。
冯诺依曼体系,梯度下降
cpu>CPU1级>2级>3级缓存>内存>IO设备
详细说:
CPU–>>内存的1级CPU独享缓存–CPU独享二级缓存–多核CPU共享三级缓存–>>内存–>>IO设备
动态语言和静态语言
静态语言一旦定义类型,就不能变化了
动态语言不用事先声明类型,随时可以复制为其它类型,没有做类型约束,上线后容易出问题。
隐式类型转换
Python基础语法
数字运算
数值类型
- 整数int:Python3不再区分int和long,long被重命名为int所以,只有int类型了。
- 进制表示方法:10 进制 10; 16进制0xa;八进制0o10;二进制0b10。
- 进制函数:bin() oct() hex()
- 浮点数float,对等于c的double类型
- 复数complex
-
- Bool属于int的子类,只有True和False两个实例。
加减乘除
加+、减-、乘*、整除/、//向下取整、%取模、**取幂
注:python2中/和//都是整除
字符串处理
- ‘’’ 三引号可以换行’’’
r和f前缀
r前缀:字符前加r或者R,表示该字符串不做特殊处理:
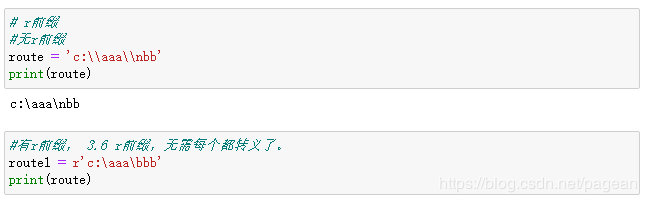
f前缀:格式化字符串输出
a =1
b =2
f"{a}的朋友是{b}"
>>> '1的朋友是2'
转义序列
\ \t \r \n ’ "
前缀r,把里面所有字符当做普通字符对待,转义字符不再转义。
续行
行尾使用, 注意\之后处理紧跟换行之外,不能有其它字符。
括号不支持跨行。
标识符
- 即以前称谓的变量名。
- 以字母、数字和下划线为组成,字母开头;不能数字开头。
- 没有常量。(只有字面量常量,比如1,‘abc’)
进制
每8位(bit)为一个字节byte。
一个字节能表示整数的范围:
- 无符号数即 216 -1=255
- 有符号数,包含127个正数和127个负数,加上0,也是255种。
转为10进制,按位乘以权,累加求和。
二进制种最低位为1,一定是奇数,最低位为0一定是偶数。
二进制转16进制
每4位一断:
| 二进制 | 十六进制 |
|---|---|
| 1000 0000 | 8 0 |
| 特殊二进制0b | 十进制 | 十六进制0x |
|---|---|---|
| 1 | 1 | 1 |
| 11 | 3 | 3 |
| 111 | 7 | 7 |
| 1111 | 15 | F |
| 1 1111 | 31 | 1F |
| 11 1111 | 63 | 3F |
| 111 1111 | 127 | 7F |
| 1111 1111 | 255 | FF |
| 1 0000 0000 | 256 | 100 |
特殊十六进制记忆
| 特殊十六进制0x | 十进制 |
|---|---|
| 9 | 9 |
| A | 10 |
| D | 13 |
| 10 | 16 |
| 20 | 32 |
| 30 | 48 |
| 31 | 49 |
| 41 | 65 |
| 61 | 97 |
| 7F | 127 |
| FF | 255 |
| FE | 254 |
二进制转8进制,每3位一断:
| 二进制 | 八进制 |
|---|---|
| 10 000 000 | 2 0 0 |
十六、八进制转二进制
- 十六进制转二进制,按位展开即可,
例如0xF8, 得二进制0b 1111 1000 - 八进制转二进制,按位展开即可,
例如0o664,得二进制0b 110 110 100
十进制转2、8、16进制
- 十进制转二进制
除以基数2,直到商为0,反向提取余数。 - 十进制转八进制
除以基数8,直到商为0,反向提取余数。 - 十进制转十六进制
除以基数16,直到商为0,反向提取余数。
码制
原码
原码:把生活应该有的正负概念,原原本本的表示出来。把左边第一位腾出位置,存放符号,正用0来表示,负用1来表示。
反码
反码:但使用“原码”储存的方式,方便了看的人类,却苦了计算机。例如,我们希望 (+1)和(-1)相加是0,但计算机只能算出0001+1001=1010 (-2)。 为了解决“正负相加等于0”的问题,在“原码”的基础上,人们发明了“反码”。
“反码”表示方式是用来处理负数的,符号位置不变,其余位置相反。
就算计无需算原码:0001+1001=1010 (-2);只需算反码:0001+1110=1111,刚好反码表示方式中,1111象征-0。
补码
(+1)和(-1)相加,变成了0001+1101=1111,刚好反码表示方式中,1111象征-0人们总是进益求精,历史遗留下来的问题—— 有两个零存在,+0 和 -0我们希望只有一个0,所以发明了"补码",同样是针对"负数"做处理的"补码"的意思是,从原来"反码"的基础上,补充一个新的代码,(+1)

有得必有失,在补一位1的时候,要丢掉最高位我们要处理"反码"中的"-0",当1111再补上一个1之后,变成了10000,丢掉最高位就是0000,刚好和左边正数的0,完美融合掉了这样就解决了+0和-0同时存在的问题另外"正负数相加等于0"的问题,同样得到满足举例,3和(-3)相加,0011 + 1101 =10000,丢掉最高位,就是0000(0)。
简述:
- 原码呢,就是后面不动,第一位表示符号。5是0101,-5是1101.优点是,人能直接念出来1101是-5。缺点呢,你把0101和1101加起来,是啥?反正和0没啥关系吧…对,缺点就是没法直接加。
- 反码的负数是把原码“符号位不变,数值位取反”。如-5原码是1101,所以它的反码就是1010;老师只给了一行课件,我跟它真的不熟,我不知道他有什么用,个人揣测它是原码到补码的一种过渡形态。也就是说,我们可以快速从反码知道原码和补码。
- 补码,用补码表示负数就是反码+1。-5的反码是1010,所以它的补码就是1011。它的优点是,可以把负数直接拿来算加法。
| 码 | 规则 | 正数- | 负数 |
|---|---|---|---|
| 原码 | 左边第一位腾出位置,存放符号,正用0来表示,负用1来表示。 | 0110 1100 | 1110 1100 |
| 反码 | 计算机使用:反码可由原码得到。如果机器数是==正数,则该机器数的反码与原码一样==;如果机器数是负数,则该机器数的反码是对它的 原码符号位不变,各位取反而得到的。 | 0110 1100 | 1001 0011 |
| 补码 | 为给人看的:补码可由原码得到。如果机器数是==正数,则该机器数的补码与原码一样==;如果机器数是负数,则该机器数的补码是对它的原码符号位不变,各位取反,并在未位加1,即反码+1而得到补码的补码就是原码 | 0110 11000 | 1001 0100 |
补码求原码
已知一个数的补码,求原码的操作分两种情况:
如果补码的符号位为“0”,表示是一个正数,所以补码就是该数的原码。
如果补码的符号位为“1”,表示是一个负数,求原码的操作可以是:符号位为1;其余各位取反,然后再整个数加1。
补码加、减运算公式
在做补码加减法时,只需将符号位和数值部分一起参与运算,并且将符号位产生的进位丢掉即可。
补码加法公式
[X+Y]补 = [X]补 + [Y]补
补码减法公式
[X-Y]补 = [X]补-[Y]补 = [X]补 + [-Y]补
其中:[-Y]补称为负补,求负补的办法是:对补码的每一位(包括符合位)求反,且未位加1.
假设字长为8的计算机sbyte类型所能表示的最大数是11111111,若再加1称为100000000(9位),但因只有8位,最高位1自然丢失。又回了00000000,所以字长为8的二进制系统的模为2^8。
详解阅读推荐:
张子秋博客
知乎趣味讨论
思考题1:内存中如果看0xFF,这个数一定是255吗?
不一定,如果是无符号数,才是255. 在计算机中,负整数就是由补码存储的。
例如 5-1,即5+(-1)
0000 0101 -->5的原码
1111 1111 -->-1的补码
---------------------------
0000 0101 --结果是4 (溢出位删除)
运算符
比较运算符
支持链式比较: 4>3>2
成员运算符
in, not in
身份运算符
is , is not
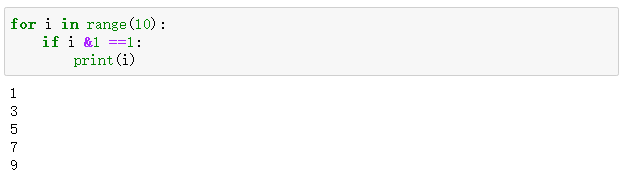
位运算
&: 位与;
|:位或
^:异或
<<:左移
>>: 右移
~:按位取反,包括符号位
内存操作会用到,举例5&3=1:
0000 0101
0000 0011 &与
----------------
0000 0001
5|3=7:
0000 0101
0000 0011 |或
----------------
0000 0111
5^3=6:
0000 0101
0000 0011 |异或,相异出一
----------------
0000 0110
~12 =-13
0000 1100 12
1111 0011 取反(计算机存储的是这个)
---------------------
1000 1101 为给人看,出补码的补码,即原码 -13
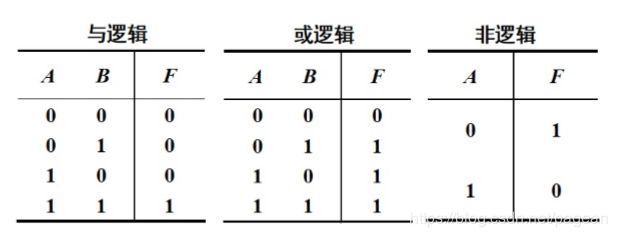
逻辑运算真值表
快速计算法 :与做乘法,或做加法(其中1+1=2->1 作为特例)。
Python运算符优先级:算数运算>比较>逻辑;not>and>or
按照这个规则,可以很容易识别如下执行顺序:
1 + 2 > 3 and 4 + 5 < 10
更详细一点: 算术运算符>位运算符>比较运算符>逻辑
单目运算符>双目运算符 -2 优先于 -2 < -1。
幂>乘除 2*2**3 =16
四则运算>移位>比较。
多用括号,避免阅读歧义
(1 + 2 > 3) and (4 + 5 < 10) #简单易懂,可以不用括号
((1 + 2 == 3) and "a" and (4 + 5 < 10) and 0) or (1 and 0) #复杂的,要用括号注释
and 要将可以短路的0值放到前面;
or要将可以短路的1值放到最前面。
2. 表达式
内置函数
Type
isinstance 的用法
False等价
False 等价布尔值,相当于 bool(value)
- 空容器
-
- 空集合set
-
- 空字典dict
-
- 空列表list
-
- 空元组tuple
空字符串
None
0
Print 的sep和end
取整运算
-
ceil向上;floor向下;
-
// 除, 向下取整
-
int只截取整数部分,正数向下取整;负数向上取整
-
round 四舍六入五取偶
惰性对象range
前包后不包。
for i in range(1,10,2):
print(i)
range倒序输出的实现:
for i in range(10,-1,-2):
print(i)
3. 分支和循环
分支语句
单分支 if
多分支 if …elif(elif隐含上一个if不成立的条件)
循环语句
for 循环的else子语句,在循环没有被break的是才执行
即,被break后,不会else
for i in range(1,10,2):
print(i)
if i > 6:
break
else:
print("这句不会被执行")
>>>
1
3
5
7
3. 线性表
线性表的类别
- 顺序表:使用一大块连续内存顺序存储的元素,这样的成为顺序表。
- 链表:是线性结构的线性表,内存分布上看着不连续,但是内部有指向,所以它是有明确的顺序的。
3.1 Python列表的操作
列表操作原理
详见: https://blog.csdn.net/pagean/article/details/104999730
3.2 Python元组的操作: 待撰
3.3 Python字典的操作 :待撰
3.4 Python集合的操作:待撰
Python入门测试
详见: https://blog.csdn.net/pagean/article/details/105043990