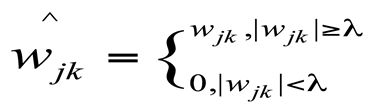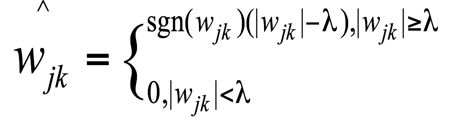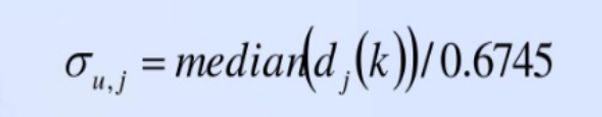小波阈值图像去噪
一、理论依据
图像和噪声在经过小波变换后具有不同的特性,因为将含噪信号在各尺度上进行小波分解后,图像的能量主要集中在低分辨率子带上,而噪声信号的能量主要分布在各个高频子带上。
原始图像信息的小波系数绝对值较大,噪声信息小波系数的绝对值较小,在这种前提下,我们可以通过设定一个合适的阈值门限,采用阈值办法保留有用信号系数。而且这个去噪的过程其实也就是对高频的小波系数进行处理的过程。
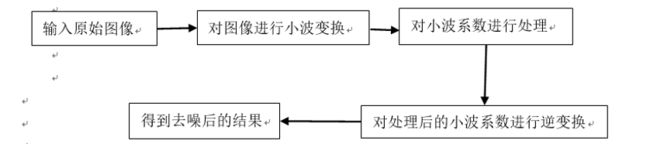
二、去噪过程
三、阈值去噪
小波阈值去噪有硬阈值去噪、软阈值去噪。
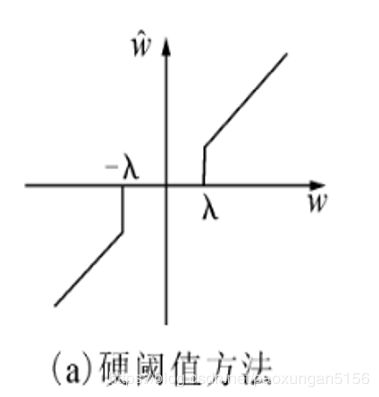
(1)硬阈值去噪
当小波系数小于某个临界阈值时,认为当时的小波系数主要是由噪声引起的,应该舍弃;当小波系数大于这个临界阈值时,认为这时的小波系数主要是由信号引起的,应该把小波系数直接保留下来。
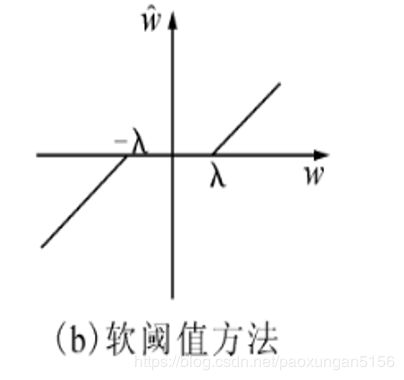
(2)软阈值去噪
进行比较含噪信号的小波系数与选定的阈值大小,大于阈值的点收缩为该点值与阈值的差值,小于阈值相反数的点收缩为该点值与阈值的和,绝对值小于等于阈值的点为0.
四、阈值的计算
目前常见的阈值计算方法有:固定阈值估计、极值阈值估计、无偏似然估计以及启发式估计等(N为信号长度)。下面介绍固定阈值计算
第一步:先求出噪声的方差
第二步:在利用固定阈值公式求出lamda.
![]()
五、算法实现
clear all;
close all;
X=imread('lena.jpg');
[height width]=size(X);
X=im2double(X);
Y1=double(X);
A=imnoise(X,'gaussian',0,0.01);
%A=imnoise(X,'salt & pepper',0.05);%加入椒盐噪声
wname='sym3 ';
n=3;
[c,s]=wavedec2(A,n,wname);
for i=1:3
step(i)=s((i+1),1)*s((i+1),2); %得到高频每层分解系数的长度
end
num(1,1)=s(1,1)*s(1,2)+1; %获取各层各高频分量在c向量中的坐标 H|V|D
num(1,2)=num(1,1)+s(2,1)*s(2,2);
num(1,3)=num(1,2)+s(2,1)*s(2,2);
num(2,1)=num(1,3)+s(2,1)*s(2,2);
num(2,2)=num(2,1)+s(3,1)*s(3,2);
num(2,3)=num(2,2)+s(3,1)*s(3,2);
num(3,1)=num(2,3)+s(3,1)*s(3,2);
num(3,2)=num(3,1)+s(4,1)*s(4,2);
num(3,3)=num(3,2)+s(4,1)*s(4,2);
%m=0.02;
C=c;
Y=c;
for i=1:3
[H,V,D]=detcoef2('a',c,s,i);%提取第i层各高频系数,提取二维信号小波分解的细节分量
B=[H V D];
[L,T]=size(B);
for k=1:L
for w=1:T
sigma=median(abs(B(k,w)))/0.6745;%噪声方差
end
end
th=sigma*sqrt(2*log10(L*T));%计算阈值 采用的是固定阈值的方法
ch=c(1,num(4-i,1):num(4-i,3)+step(4-i)-1);%确定高频系数的范围,为下一步阈值处理和更新高频系数做准备
chl=length(ch);
for j=1:chl
if abs(ch(j))>=th
ch(j)=sign(ch(j))*(abs(ch(j))-th);%软阈值处理函数
ych(j)=ch(j);
else
ch(j)=0;
ych(j)=0;
end
end
C(1,num(4-i,1):num(4-i,3)+step(4-i)-1)=ch(1,1:chl);
Y(1,num(4-i,1):num(4-i,3)+step(4-i)-1)=ych(j);
end
X0=waverec2(C,s,wname);
X1=waverec2(Y,s,wname);
A1= medfilt2(A);
disp('加噪图像信噪比为:'), sny=10*log10(sum(sum(double(X).^2))/sum(sum((double(X)-double(A)).^2)))
disp('软阈值去噪后图像信噪比为:'),sndz=10*log10(sum(sum(double(X).^2))/sum(sum((double(X)-double(X0)).^2)))
disp('硬阈值去噪后图像信噪比为:'),sndz=10*log10(sum(sum(double(X).^2))/sum(sum((double(X)-double(X1)).^2)))
disp('中值去噪后图像信噪比为:'), sndz=10*log10(sum(sum(double(X).^2))/sum(sum((double(X)-double(A1)).^2)))
figure
subplot(121);imshow(X);title('原图像')
subplot(122);imshow(A);title('添加噪声后的图像')
figure
subplot(131);imshow(X0,[]);title('软阈值去噪后图像')
subplot(132);imshow(A1);title('中值去噪后图像')
subplot(133);imshow(X1,[]);title('硬阈值去噪后图像')注:
[c,s]=wavedec2(A,n,wname);
c为各层分解系数,s为各层分解系数长度,也就是大小.
c的结构:c=[A(N)|H(N)|V(N)|D(N)|H(N-1)|V(N-1)|D(N-1)|H(N-2)|V(N-2)|D(N-2)|...|H(1)|V(1)|D(1)]
A(N)代表第N层低频系数,H(N)|V(N)|D(N)代表第N层高频系数,分别是水平,垂直,对角高频,以此类推,到H(1)|V(1)|D(1).
s的结构:是储存各层分解系数长度的
即第一行是A(N)的长度(其实是A(N)的原矩阵的行数和列数),第二行是H(N)|V(N)|D(N)|的长度,第三行是H(N-1)|V(N-1)|D(N-1)的长度,倒数第二行是H(1)|V(1)|D(1)长度,最后一行是X的长度(大小)。
具体参见链接 https://blog.csdn.net/afgh2587849/article/details/6020560