工业机器人运动轨迹规划方法简述

Thanks John J. Craig for his great work of Introduction to Robotics - Mechanics and Control - 3rd Edition.

工业机器人的运动轨迹

1. 点到点运动：不需要在笛卡尔空间规划末端运动轨迹，机器人各个关节运动不需要联动。
2. 轨迹跟踪运动：以点到点为基础，各个关节运动需要联动。

一般而言，运动包括工具相对于工作台的姿态变化和位置变化。

关节空间运动规划

目标：使关节空间轨迹平滑。
一般情况下，关节空间的规划方法便于计算，并且由于关节空间与笛卡尔空间之间并不存在连续的对应关系，因而不会发生机构的奇异性问题。

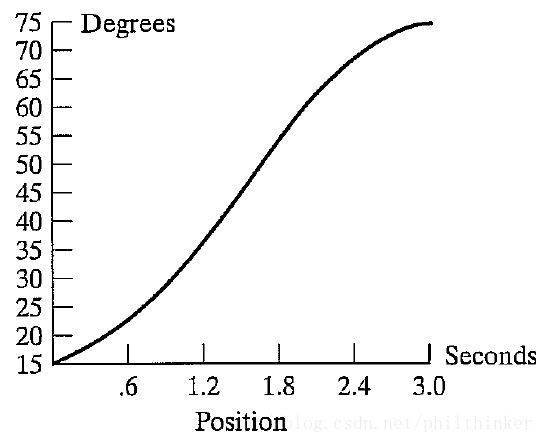
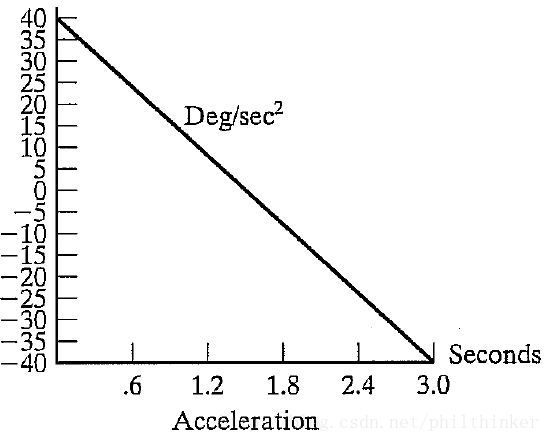
3次多项式插值

做如下假设：某个关节从 t0 时刻的位置 q0 运动到 tf 时刻的位置 qf 。在 t0 和 tf 时刻速度均为0。

q(0)=q0,q(tf)=qf,q˙(0)=0,q˙(tf)=0

利用3次多项式来拟合轨迹：

q(t)=a0+a1t+a2t2+a3t3q˙(t)=a1+2a2t+3a3t2q¨(t)=2a2+6a3t

将边界条件代入即可解出参数 a1,…,a3 。

过路径点的3次多项式插值

假设起点与终点的关节速度不为0时，利用3次多项式进行插值。解法同上，不再赘述。
需要注意，选择路径点的关节速度时，要考虑到保证每个路径点的加速度是连续的。

高阶多项式插值

当考虑到机器人关节空间起始点和目标点的加速度时，需采用高阶多项式插值。即修改边界条件为：

q(0)=q0，q˙(0)=q˙0，q¨(0)=q¨0，q(tf)=qfq˙(tf)=q˙fq¨(tf)=q¨f

因此，6个边界条件对应高阶多项式的6个系数， a0,…,a5 。

q(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

用抛物线过渡的线性插值

直接进行线性插值会导致起始点和终止点的关节运动速度不连续，因此我们可以在中间利用直线线性插值，两端利用抛物线过渡。利用直线段求出关节速度：

q˙tb=qh−qbth−tb

其中 th 为中间时刻， tb 为过渡时刻， qh 为中间位置。假设关节加速度 q¨ 已知，则

qb=q0+12q¨t2b

且我们知道：

q˙b=q¨tb

因此我们可以利用上述3式解出

tb=ff2−q¨2t2f−4q¨(qf−q0)−−−−−−−−−−−−−−√2q¨

为了保证直线存在，加速度不能太小。

过路径点的抛物线过渡线性插值

将邻近路径点用直线相连，路径点附近利用抛物线过渡。求取过渡时间时可以将路径分为第一路径、中间路径和最后路径三种情况分别讨论，原理同上，不再赘述。

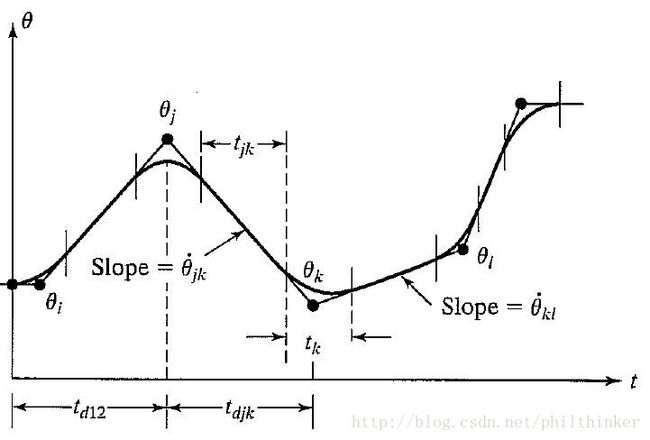
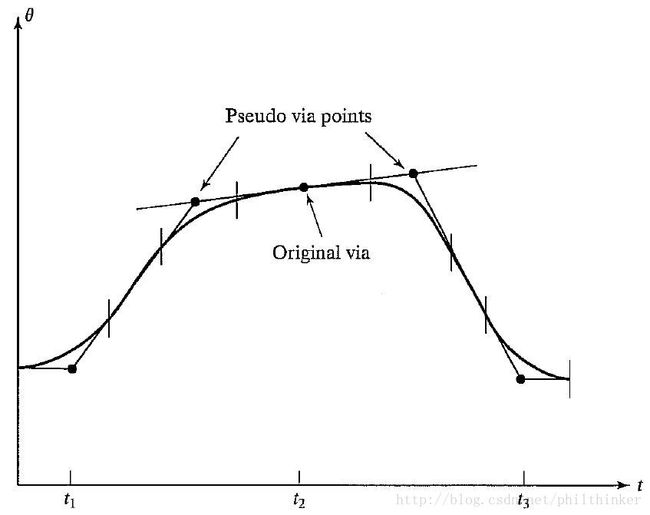
值得注意的是，多段带有抛物线拟合的直线样条曲线实际并没有经过那些中间点，除非操作臂在此处停留。如果用户需要操作臂精确经过某个中间点而不停留，仍可采用前述计算公式，但是需要做如下补充：将操作臂希望经过的中间点替换为位于其两侧的两个伪中间点。

B样条插值

首先简要介绍下B样条：
设 m 为样条的次数，在 m+1 个子区间以外的其他子区间上， B样条的取值均为0。 B样条函数可以采用递归的方式进行定义。假设对于自变量 x 有 m+2 个点 xi,xi+1,…,xi+m+1 构成 m+1 个子区间。首先定义 0 次B样条函数：

Ni,0(x)={1,0,x∈[xi.xi+1)x∉[xi,xi+1)

对于 m 次B样条：

Ni,m(x)=x−xixi+m−xiNi,m−1(x)+xi+m−1−xxi+m−1−xi+1Ni+1,m−1(x)

在区间 [x0,xk] 内的任意函数，可以表达为利用第 m 次B样条函数作为基函数的加权和：

f(x)=∑i=−mkaiNi.m(x)

上式包含了 k+m+1 个参数 a 。在每个子区间上，最多为 m+1 个B样条函数的加权和。在进行曲线插值或拟合时，需要确定这 k+m+1 个参数。

有时候为了消除在非期望点的波动，可以利用相邻期望点的中间点作为控制点。

B样条的主要特点是在局部的修改不会引起样条形状的大范围变化。

笛卡尔空间运动规划

笛卡尔空间的路径规划，就是计算机器人在给定路径上各点处的位置与姿态。
在关节空间中计算出的路径可保证操作臂能够到达中间点和目标点，即使这些路径点事用笛卡尔坐标系来规定的。不过，末端执行器在空间的路径不是直线，而且，其路径的复杂程度取决于操作臂特定的运动学特征。

位置规划

对于直线运动：

P(i)=P1+αi

其中 P 是位置， α 为步长。

对于圆弧运动：
假设圆弧由 P1,P2,P3 点构成，首先利用2平面的交点确定圆心位置，进而计算出半径。利用矢量相加一步步规划出 P1 到 P3 每个中间点的位置。

姿态规划

假设机器人在起始位置的姿态为 R1 ，在目标位置的姿态为 R2 ，则机器人需要调整的姿态 R 为：

R=RT1R2

利用通用旋转变换求取等效转轴与转角，进而求取机器人第 i 步相对于初始姿态的调整量。

在笛卡尔空间中，将机器人的第 i 步的位置与姿态相结合，得到机器人第 i 步的位置与姿态矩阵：

T(i)=(RiR(i)0P(i)1)

在规划和生成笛卡尔空间直线路径时，最好使用带有抛物线拟合的直线样条函数。然而，如果在每个中间点将姿态定义成旋转矩阵，则无法对其分量进行线性插值，因为这样做不一定总能得到有效的旋转矩阵。

笛卡尔路径的几何问题

1.不可达的中间点：尽管操作臂的起始点和目标点都在其工作空间内部，但是很有可能在连接这两点的直线上有些点不在工作空间中。

2.在奇异点附近的高关节速率：在某些未知处无法用有限的关节速度来实现末端执行器在笛卡尔空间的期望速度。

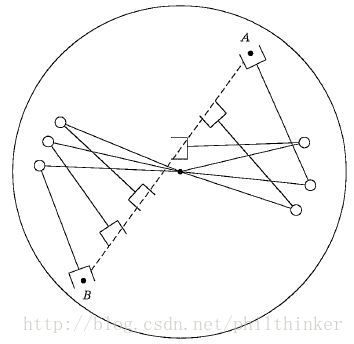
3.不同解下的可达起点和终点：如下图所示，两杆操作臂的两个杆长度相同，但是关节存在约束，这使得机器人到达空间给定点的解数量减少。