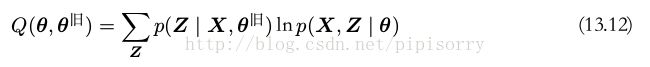HMM:隐马尔科夫模型 - 学习
http://blog.csdn.net/pipisorry/article/details/50722376
隐马尔科夫模型的三个问题
例子
举个常见的例子来引出下文,同时方便大家理解!比如我在不同天气状态下去做一些事情的概率不同,天气状态集合为{下雨,阴天,晴天},事情集合为{宅着,自习,游玩}。假如我们已经有了转移概率和输出概率,即P(天气A|天气B)和P(事情a|天气A)的概率都已知道,那么则有几个问题要问(注意,假设一天我那几件事情中的一件),
1.假如一周内的天气变化是 下雨->晴天->阴天->下雨->阴天->晴天->阴天,那么我这一周 自习->宅着->游玩->自习->游玩->宅着->自习的概率是多大?
2.假如我这一周做事序列是 自习->宅着->游玩->自习->游玩->宅着->自习,不知道天气状态的情况下这个做事序列的概率是多大?
3.假如一周内的天气变化是 下雨->晴天->阴天->下雨->阴天->晴天->阴天,那我们这一周最有可能的做事序列是什么?
4.假如我这一周做事序列是 自习->宅着->游玩->自习->游玩->宅着->自习,那么这一周的天气变化序列最有可能是什么?
wiki上一个关于HMM三个基本问题解释的例子 [wikipedia:隐马尔可夫模型]
HMM的三个基本问题
1. 给定模型(五元组),求某个观察序列O的概率(样例问题2)。
2. 给定模型和观察序列O,求可能性最大的隐藏状态序列(样例问题4)。
3. 对于给定的观察序列O,调整HMM的参数,使观察序列出现的概率最大。
一旦一个系统可以作为HMM被描述,就可以用来解决三个基本问题。
其中前两个是模式识别的问题:给定HMM求一个观察序列的概率(评估);搜索最有可能生成一个观察序列的隐藏状态序列(解码)。第三个问题是给定观察序列生成一个HMM(学习)。
a) 评估(Evaluation)
考虑这样的问题,我们有一些描述不同系统的隐马尔科夫模型(也就是一些( pi,A,B)三元组的集合)及一个观察序列。我们想知道哪一个HMM最有可能产生了这个给定的观察序列。例如,对于海藻来说,我们也许会有一个“夏季”模型和一个“冬季”模型,因为不同季节之间的情况是不同的——我们也许想根据海藻湿度的观察序列来确定当前的季节。
我们使用前向算法(forward algorithm)来计算给定隐马尔科夫模型(HMM)后的一个观察序列的概率,并因此选择最合适的隐马尔科夫模型(HMM)。
在语音识别中这种类型的问题发生在当一大堆数目的马尔科夫模型被使用,并且每一个模型都对一个特殊的单词进行建模时。一个观察序列从一个发音单词中形成,并且通过寻找对于此观察序列最有可能的隐马尔科夫模型(HMM)识别这个单词。
b) 解码( Decoding)
给定观察序列搜索最可能的隐藏状态序列。
另一个相关问题,也是最感兴趣的一个,就是搜索生成输出序列的隐藏状态序列。在许多情况下我们对于模型中的隐藏状态更感兴趣,因为它们代表了一些更有价值的东西,而这些东西通常不能直接观察到。
考虑海藻和天气这个例子,一个盲人隐士只能感觉到海藻的状态,但是他更想知道天气的情况,天气状态在这里就是隐藏状态。
我们使用Viterbi 算法(Viterbi algorithm)确定(搜索)已知观察序列及HMM下最可能的隐藏状态序列。
Viterbi算法(Viterbi algorithm)的另一广泛应用是自然语言处理中的词性标注。在词性标注中,句子中的单词是观察状态,词性(语法类别)是隐藏状态(注意对于许多单词,如wind,fish拥有不止一个词性)。对于每句话中的单词,通过搜索其最可能的隐藏状态,我们就可以在给定的上下文中找到每个单词最可能的词性标注。
C)学习(Learning)
根据观察序列生成隐马尔科夫模型。
第三个问题,也是与HMM相关的问题中最难的,根据一个观察序列(来自于已知的集合),以及与其有关的一个隐藏状态集,估计一个最合适的隐马尔科夫模型(HMM)。
当矩阵A和B不能够直接被(估计)测量时,前向-后向算法(forward-backward algorithm)被用来进行学习(参数估计),这也是实际应用中常见的情况。
针对以下三个问题,人们提出了相应的算法
1 评估问题: 前向算法
2 解码问题: Viterbi算法
3 学习问题: Baum-Welch算法
也就是隐马尔科夫模型通常解决的问题包括:
1. 对于一个观察序列匹配最可能的系统——评估,使用前向算法(forward algorithm)解决;
2. 对于已生成的一个观察序列,确定最可能的隐藏状态序列——解码,使用Viterbi 算法(Viterbi algorithm)解决;
3. 对于已生成的观察序列,决定最可能的模型参数——学习,使用前向-后向算法(forward-backward algorithm)解决。
某小皮
HMM的参数学习
HMM的学习问题就是根据观察序列生成隐马尔科夫模型。根据一个观察序列(来自于已知的集合),以及与其有关的一个隐藏状态集,估计一个最合适的隐马尔科夫模型(HMM),也就是确定对已知序列描述的最合适的参数θ = {π, A, φ}。
监督学习算法
假设已给训练数据包含S个长度相同的观测序列和对应的状态序列{(O1, I1), (O2, I2),..., (Os, Is)},那么可以利用极大似然估计法来估计隐马尔可夫模型的参数。
1,转移概率aij的估计
设样本中时刻t处于状态i,时刻t+1处于状态j的频数为Aij,那么状态转移概率aij的估计是
2,观测概率bj(k)的估计
设样本中状态为j且观测为k的频数是Bjk,那么状态为j且观测为k的概率bj(k)的估计是
3,初始状态概率πi的估计为S个样本中初始状态为qi的频率。
由于监督学习需要使用训练数据,而人工标注训练数据往往代价很高,所以有时会利用非监督学习的方法。
非监督学习算法:EM算法
如果我们观测到一个数据集 X = {x 1 , . . . , x N } ,那么我们可以使用最大似然法确定 HMM 的参数。似然函数通过对联合概率分布(13.10)中的潜在变量进行求和的方式得到,即
由于联合概率分布 p(X, Z | θ) 无法在 n 上进行分解(与混合概率分布的讨论不同),因此我们不能独立地在每个 z n 上进行求和。我们也不能显示地完成这个求和,因为有 N 个变量需要求和,每个都有 K 个状态,从而总计有 K N 个求和项。因此求和式中的项的数量随着链的长度指数增长。事实上,公式(13.11)中的求和对应于在图13.7的晶格图中通过指数多条路径进行的求和。
![]()
用于HMM的最大似然法
于是我们使用期望最大化算法(EM算法)来寻找对隐马尔可夫模型中似然函数进行最大化的有效框架。 EM 算法的开始阶段是对模型参数的某些初始的选择,我们记作 θ 旧 。在 E 步骤中,我们使用这些参数找到潜在变量的后验概率分布 p(Z | X, θ 旧 ) 。然后,我们使用这个后验概率分布计算完整数据似然函数的对数的期望,得到了一个关于参数 θ 的函数 Q(θ, θ 旧 ) ,定义为
引 入 一 些 记 号:我 们 使 用 γ(z n ) 来 表 示 潜 在 变 量 z n 的 边 缘 概 率 分 布, 用 ξ(z n−1 , z n ) 表示两个连续的潜在变量的联合后验概率分布,即
对于每个 n 值,我们可以使用 K 个非负数来存储 γ(z n ) ,这些数的和等于1。类似地,我们可以使用一个由非负数组成的 K × K 的矩阵来存储 ξ(z n−1 , z n ) ,同样加和等于1。我们也会使用 γ(z nk ) 来表示 z nk = 1 的条件概率,类似地使用 ξ(z n−1,j , z nk ) 来表示后面介绍的另一个概率。由于二值随机变量的期望就是取值为1的概率,因此我们有
如果我们将公式(13.10)的联合概率分布 p(X, Z | θ) 代入状态空间模型[顺序数据:状态空间模型 ]公式(13.12),使用 γ 和 ξ 的定义,我们有
交替进行 E 步骤和 M 步骤,直到满足某些收敛准则,例如似然函数的变化低于某个阈值。
E步骤
目标是高效地计算 γ(z n ) 和 ξ(z n−1 , z n ) ,即使用后面的前向后向算法。
M 步骤
我们关于参数 θ = {π, A, φ} 最大化 Q(θ, θ 旧 ) ,其中我们将 γ(z n ) 和 ξ(z n−1 , z n ) 看做常数。
关于 π 和 A 的最大化:
使用拉格朗日乘数法很容易求出结果为
π 和 A 的初始值:一个典型的初始化步骤是在满足加和限制和非负限制的条件下,为这些参数随机选择初始值。注意,对于从左到右的模型的情形,我们无需对 EM 的结果进行特别的修改,只需在 A jk 的适当的元素设置为零即可,因为这些元素在接下来的 EM 更新中也会保持为零。
关于 φ k 最大化 Q(θ, θ 旧 ):
在高斯发射密度的情形下,我们有 p(x | φ k ) = N (x | μ k , Σ k ) ,最大化函数 Q(θ, θ 旧 ) 可得
对于观测变量服从离散多项式分布的情形,观测变量的条件概率分布为
对于服从伯努利分布的观测变量,可以得到类似的结果。
发射概率分布的参数的初始值:
1 一种设置的方式是首先将数据集看成独立同分布的,然后通过最大似然方法调节发射概率密度,之后使用得到的值来初始化 EM 的参数。
2 参数 φ 的初始化依赖于概率分布的形式。对于高斯分布的情形,参数 μ k 可以通过对数据使用 K 均值算法进行初始化, Σ k 可以使用对应的 K 均值聚类的协方差矩阵初始化。
前向后向算法
EM 算法中的 E 步骤,计算 γ(z nk ) 和 ξ(z n−1,j , z nk ) 的高效的方法 。在隐马尔可夫模型这一特定的问题中,这个被称为前向后向算法( forward-backward )算法( Rabiner, 1989 ),或者 Baum-Welch 算法( Baum, 1972 )。其中有很多变体,使用最多的是alpha-beta算法。
首先给出一些条件独立性质( Jordan, 2007 )
其中 X = {x 1 , . . . , x N } 。
这些关系很容易使用 d -划分证明。例如在第二个结果中,我们注意到结点 x 1 , . . . , x n−1 中的任何一个结点到结点 x n 的路径都要通过结点 z n ,它被观测到。由于所有这种路径都是头到尾的,因此这个条件独立性质一定成立。
计算 γ(z nk )
在给定观测数据 x 1 , . . . , x N 的条件下,计算 z n 的后验概率分布 p(z n | x 1 , . . . , x N ) 。这表示一个长度为 K 的向量,它的项对应于 z nk 的期望值。
α(z n ) 表 示 观 测 到 时 刻 n 及 其 之 前 时 刻 的 所 有 数 据 和 z n 的 值 的 联 合 概 率, 而 β(z n ) 表 示 在 给定 z n 的条件下,从时刻 n + 1 到 N 的所有未来数据的条件概率。
高效计算 α(z n ) 和 β(z n ) 的递归关系
α(z n ) 的递归关系
使用公式(13.34)给出的 α(z n ) 的定义,我们有
α 递归的每一步的计算代价为 O(K 2 ) 。
初始条件,形式为
这表明对于 k = 1, . . . , K , α(z 1k ) 的值为 π k p(x 1 | φ k ) 。整体代价是 O(K 2 N ) 。
β(z n ) 的递归关系
起始条件对于所有的 z N 都有 β(z N ) = 1。
Note: M 步方程中, p(X) 可以消去.然而, p(X) 表示似然函数,我们通常在 EM 优化过程中能够监视它的值,比如收敛的判断。
然后使用 n = N 的结果,利用 β(z N ) 是一个元素全部为1的向量这一事实。
通过将似然函数表示为(13.42)的形式,我们将计算代价从关于链长度的指数量级减小到了线性量级,方法是交换了加和与乘积的顺序,从而在每个时间步骤 n 中,我们对通过每个状态 z nk 的所有路径的贡献进行求和,得到了中间的量 α(z n ) 。
ξ(z n−1 , z n ) 的计算
可以使用 α 和 β 的递归结果直接计算 ξ(z n−1 , z n ) 。
我们已经讨论了使用最大似然方法估计 HMM 的参数。这个框架很容易推广到正则化的最大似然函数,方法是引入模型参数 π, A 和 φ 上的先验概率分布,然后通过最大化后验概率的方式估计参数的值。此外,我们可以使用变分方法,得到 HMM 的一个纯粹的贝叶斯方法,其中我们对参数概率分布进行积分或求和( MacKay, 1997 )。
某小皮
HMM 的加和-乘积算法
可以使用加和-乘积算法来求解寻找局部边缘概率的问题。毫不令人惊讶的事实是,这等价于前一节讨论的前向-后向算法,因此加和-乘积算法给我们提供了一种简单的方式推导 alpha-beta 递归公式。
将图13.5所示的有向图变换为因子图,简化因子图表示。
推导过程详见[PRML]。
缩放因子
在 实 际 应 用 中 使 用 前 向 后 向 算 法 之 前, 注 意 到 在 每 一 步 中, 新 的 值 α(z n ) 为 前 一 个 值 α(z n−1 ) 乘以 p(z n | z n−1 ) 和 p(x n | z n ) 。 由 于 这 些 概 率 通 常 远 远 小 于 1, 因 此 随 着 我 们 沿 着 链 向 前 推进, α(z n ) 很快就会指数地趋近于零。对于中等的链长度(例如100左右), α(z n ) 的计算很快就会超出计算机的计算范围,即使使用双精度浮点数也是如此。
定义 α 的一个归一化的版本
α^bar的递归方程
β^bar的递归结果
似然函数
边缘概率
from:http://blog.csdn.net/pipisorry/article/details/50722376
ref: [PRML]