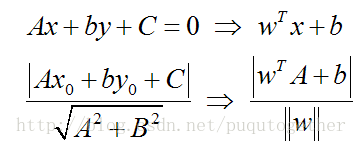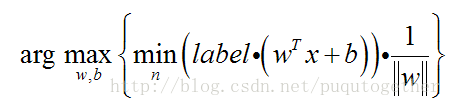理解SVM(一)——入门SVM和代码实现
理解SVM
这篇博客我们来理解一下SVM。其实,之前好多大牛的博客已经对SVM做了很好的理论描述。例如CSDN上july的那篇三层境界介绍SVM的博文,连接如下:
http://blog.csdn.net/v_july_v/article/details/7624837
那么我这里抛去一些复杂的公式推导,给出一些SVM核心思想,以及用Python实现代码,再加上我自己的理解注释。
1. SVM的核心思想
SVM的分类思想本质上和线性回归LR分类方法类似,就是求出一组权重系数,在线性表示之后可以分类。我们先使用一组trainging set来训练SVM中的权重系数,然后可以对testingset进行分类。
说的更加更大上一些:SVM就是先训练出一个分割超平面separation hyperplane, 然后该平面就是分类的决策边界,分在平面两边的就是两类。显然,经典的SVM算法只适用于两类分类问题,当然,经过改进之后,SVM也可以适用于多类分类问题。
我们希望找到离分隔超平面最近的点,确保它们离分隔面的距离尽可能远。这里点到分隔面的距离被称为间隔margin. 我们希望这个margin尽可能的大。支持向量support vector就是离分隔超平面最近的那些点,我们要最大化支持向量到分隔面的距离。
那么为了达到上面的目的,我们就要解决这样的一个问题:如何计算一个点到分隔面的距离?这里我们可以借鉴几何学中点到直线的距离,需要变动的是我们这里是点到超平面的距离。具体转换过程如下:
除了定义距离之外,我们还需要设定两类数据的类别标记分别为1和-1,这样做是因为我们将标记y和距离相乘,不管属于哪一类,乘积都是一个正数,这样有利于我们设计目标函数。
这样我们便可以定义我们SVM的目标函数:
求解这个问题需要经过一系列的转换。具体如下:
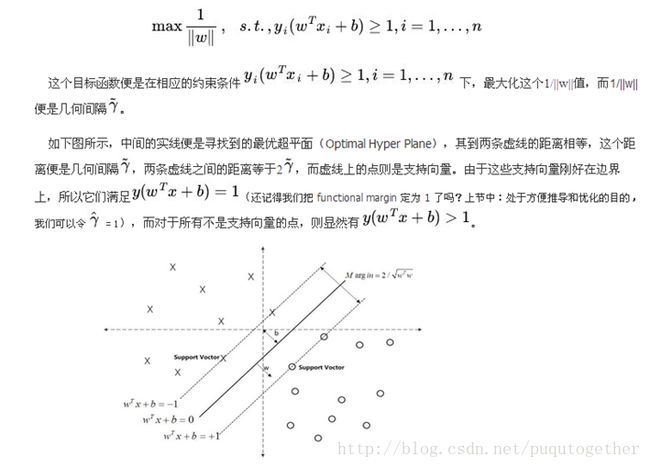
SMO算法的目标是求出一系列alpha和b,一旦求出了这些alpha,就很容易计算出权重向量w,并得到分隔超平面。SMO的工作远离是:每次循环中选择两个alpha进行优化处理,一旦找到一对合适的alpha,那么就增大其中一个,同时减小另一个。选择的alpha要满足在间隔边界之外的条件,而且还没有进行过区间化处理或者不再边界上。
《机器学习实战》中给出了利用Python实现SVM的代码,我加了一些注释便于理解,如下:
from numpy import *
import random
def loadDataSet(fileName): #构建数据库和标记库
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2])) #只有一列
return dataMat, labelMat
def selectJrand(i, m): #生成一个随机数
j=i
while(j==i):
j=int(random.uniform(0, m)) #生成一个[0, m]的随机数,int转换为整数。注意,需要import random
return j
def clipAlpha(aj, H, L): #阈值函数
if aj>H:
aj=H
if ajtoler) and (alphas[i]>0)):
j=selectJrand(i, m) #从m中选择一个随机数,第2个alpha j
fXj=float(multiply(alphas, labelMat).T*dataMatrix*dataMatrix[j, :].T)+b
Ej=fXj-float(labelMat[j])
alphaIold=alphas[i].copy() #复制下来,便于比较
alphaJold=alphas[j].copy()
if(labelMat[i]!=labelMat[j]): #开始计算L和H
L=max(0, alphas[j]-alphas[i])
H=min(C, C+alphas[j]-alphas[i])
else:
L=max(0, alphas[j]+alphas[i]-C)
H=min(C, alphas[j]+alphas[i])
if L==H:
print 'L==H'
continue
#eta是alphas[j]的最优修改量,如果eta为零,退出for当前循环
eta=2.0*dataMatrix[i, :]*dataMatrix[j, :].T-\
dataMatrix[i, :]*dataMatrix[i, :].T-\
dataMatrix[j, :]*dataMatrix[j, :].T
if eta>=0:
print 'eta>=0'
continue
alphas[j]-=labelMat[j]*(Ei-Ej)/eta #调整alphas[j]
alphas[j]=clipAlpha(alphas[j], H, L)
if(abs(alphas[j]-alphaJold)<0.00001): #如果alphas[j]没有调整
print 'j not moving enough'
continue
alphas[i]+=labelMat[j]*labelMat[i]*(alphaJold-alphas[j]) #调整alphas[i]
b1=b-Ei-labelMat[i]*(alphas[i]-alphaIold)*\
dataMatrix[i, :]*dataMatrix[i, :].T-\
labelMat[j]*(alphas[j]-alphaJold)*\
dataMatrix[i, :]*dataMatrix[j, :].T
b2=b-Ej-labelMat[i]*(alphas[i]-alphaIold)*\
dataMatrix[i, :]*dataMatrix[j, :].T-\
labelMat[j]*(alphas[j]-alphaJold)*\
dataMatrix[j, :]*dataMatrix[j, :].T
if(0alphas[i]):
b=b1
elif(0alphas[j]):
b=b2
else:
b=(b1+b2)/2.0
alphaPairsChanged+=1
print 'iter: %d i: %d, pairs changed %d' %(iter, i, alphaPairsChanged)
if(alphaPairsChanged==0):
iter+=1
else:
iter=0
print 'iteration number: %d' %iter
return b, alphas
if __name__=="__main__":
dataArr, labelArr=loadDataSet('testSet.txt')
b, alphas=smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
print b, alphas 还有其他语言实现的SVM,可以在下面网站中找到,以及一些注释:
http://www.csie.ntu.edu.tw/~cjlin/libsvm/
http://www.pami.sjtu.edu.cn/people/gpliu/document/libsvm_src.pdf