LeetCode 5 (Longest Palindromic Substring)
###Longest Palindromic Substring(最大回文字符串)
####1、题目描述:
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example 1:
Input: “babad”
Output: “bab”
Note: “aba” is also a valid answer.
Example 2:
Input: “cbbd”
Output: “bb”
给出一个字符串s,找出长度最大的回文子串,s的最大长度小于1000。
####2、摘要:
下面介绍了几种方法实现:回文,动态规划和字符串操作。回文的定义:**一个字符串从两个方向读,它的内容是相同的。**例如:**S = "aba"是回文字符串,而S = “abc”**不是回文字符串。
####3、解决方法:
######方法1:Brute Force(暴力破解)
很明显,暴力破解就是找到所有子串验证它是否是回文字符串。
Java实现:
public boolean isPalindrome(String s) {
String ss = new StringBuilder(s).reverse().toString();
if (ss.equals(s)) {
return true;
}
return false;
}
public String longestPalindrome(String s) {
int longestLength = 0;
String longestSubString = "";
for (int i = 0; i < s.length(); i++) {
for (int j = i+1; j <= s.length(); j++) {
String subString = s.substring(i,j);
if (isPalindrome(subString) && subString.length()>longestLength){
longestLength = subString.length();
longestSubString = subString;
}
}
}
return longestSubString;
}
时间复杂度:
两个for循环中嵌套了一个判断回文的过程,回文判断我使用的是StringBuilder的reverse()方法,时间复杂度一共是O(n^3)。比较不理想,提交上去会出现时间超时。
空间复杂度:两个变量,复杂度为O(1)。
######方法2:Longest Common Substring(最长的公共子串)
一些人可能会想出一个最快的方法,倒序字符串s,然后与原字符串对比,然后找出最长的公共子串,这个子串一定就是最长的回文子串。
从表面上看这个方法是正确的,但是仔细想来并不是完全正确,例如S = “abacdfgdcaba”,他和倒序的公共最长字符为 “abacd”,然而这个并不是回文字符串。导致出现这个情况的原因是原字符串中存在一个非回文倒序副本。如果要排除这个影响,就要在候选字符串中 检查子串的索引是否与反向子串的原始索引相同,相同就保留,不同就舍弃。
首先实现寻找最长的公共子串,具体步骤参考:
https://blog.csdn.net/u010397369/article/details/38979077
具体实现思路就是把两个字符串组成一个二维数组 ,如果两个对应字符相等,就执行 temp[ i ][ j ] = temp[ i - 1 ][ j - 1] + 1。因为i-1或者j-1会越界,所以可以单独处理。temp[ i ][ j ] 保存的就是公共子串的长度。
Java实现
public String longestPalindrome_2(String s) {
if (s.equals("")) {
return "";
}
String ss = new StringBuilder(s).reverse().toString(); //倒序
int longestlength = 0;
int maxEnd = 0;
int[][] temp = new int[s.length()][ss.length()];
char[] s_char = s.toCharArray();
char[] ss_char = ss.toCharArray();
//原字符串做列,倒序后的子串作为行
for (int i = 0; i < ss_char.length; i++) {
for (int j = 0; j < s_char.length; j++) {
if (s_char[i] == ss_char[j]) {
if (i == 0 || j == 0) {
temp[i][j] = 1;
} else {
temp[i][j] = temp[i - 1][j - 1] + 1;
}
}
if (temp[i][j] > longestlength) {
longestlength = temp[i][j];
maxEnd = i;
}
}
}
return s.substring(maxEnd - longestlength + 1, maxEnd + 1);
}
以上算法只能实现寻找最长的公共子串,如果s=“abc435cba”,公共子串为"abc",但是这个不是回文字符串。为了解决这个问题,我们还要对比子串在倒序后的字符串的位置和原字符串的位置是否对应。
举个例子,如果s=“caba”,s’ = “abac”,他们的最长回文串为**“aba”,“aba”**在原字符串中的位置为 1 2 3 ,在s’中的位置为 0 1 2,所以 aba 就是我们需要找的。当然我们不需要每个字符都判断,我们只需要判断末尾字符就可以。
如图:
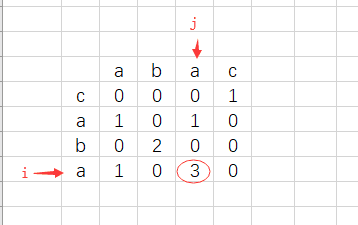
i所指的字符a在原字符串中的位置为beforeRev = length - i- 1 = 0,beforeRev就是在j中为第一个字符位置,且 beforeRev + temp[i][j] - 1 =2代表j中最后一个字符的位置,如果位置与j相等,aba就是要找的。我们可以写出如下代码:
//动态规划 (获取最长回文串) 需要和原字符对比位置
public String longestPalindrome_3(String s) {
if (s.length() <= 1) {
return s;
}
String ss = new StringBuilder(s).reverse().toString(); //倒序
int longestlength = 0;
int maxEnd = 0;
int[][] temp = new int[s.length()][ss.length()];
char[] s_char = s.toCharArray();
char[] ss_char = ss.toCharArray();
//原字符串做列,倒序后的子串作为行
for (int i = 0; i < ss_char.length; i++) {
for (int j = 0; j < s_char.length; j++) {
if (s_char[i] == ss_char[j]) {
if (i == 0 || j == 0) {
temp[i][j] = 1;
} else {
temp[i][j] = temp[i - 1][j - 1] + 1;
}
}
if (temp[i][j] > longestlength) {
/*******************增加的部分***********************/
int beforeRev = s.length() - i - 1;
if (beforeRev + temp[i][j] - 1 == j) {
longestlength = temp[i][j];
maxEnd = i;
}
}
}
}
return s.substring(maxEnd - longestlength + 1, maxEnd + 1);
}
时间复杂度:两个嵌套循环,O(n^2)
空间复杂度:一个二维数组,O(n^2)
仔细观察可以发现,我们判断字符相等的只用到了temp[i][j],一行用过之后就弃置不用了。所以我们可以把空间复杂度优化到O(n),只需要把一个一维数组重新赋值即可,因为正序赋值有可能覆盖改后面需要使用的数据
比如a[3] = a[2]+1时,计算a[4]的时候a[3]的值就不是原来的了。所以我们需要从后往前计算,代码如下:
public String longestPalindrome_4(String s) {
if (s.equals("")) {
return "";
}
String ss = new StringBuilder(s).reverse().toString(); //倒序
int longestlength = 0;
int maxEnd = 0;
int[] temp = new int[s.length()];
char[] s_char = s.toCharArray();
char[] ss_char = ss.toCharArray();
for (int i = 0; i < s_char.length; i++) { //初始化第一行
temp[i] = (s_char[0] == ss_char[i]) ? 1 : 0;
}
for (int i = 0; i < s_char.length; i++) {
for (int j = ss.length() - 1; j >= 0; j--) {
if (s_char[i] == ss_char[j]) {
if (i == 0 || j == 0) {
temp[j] = 1;
} else {
temp[j] = temp[j - 1] + 1;
}
if (temp[j] > longestlength) {
/*******************增加的部分***********************/
int beforeRev = s.length() - j - 1;
if (beforeRev + temp[j] - 1 == i) {
longestlength = temp[j];
maxEnd = i;
}
}
} else {
temp[j] = 0;
}
}
}
return s.substring(maxEnd - longestlength + 1, maxEnd + 1);
}
时间复杂度:两个嵌套循环,O(n^2)
空间复杂度:一个一维数组,O(n)
######方法3:扩展中心
我们观察到一个回文串是从一个中心到两边的镜像。所以,回文串可以从一个字符(奇数)或两个字符(偶数)的为中心拓展,它的中心总共有2n-1个。以i为中心左边为left,右边为right,先令left=right=i,满足**left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)**时,left–;right++;向外拓展,直到结束。回文的长度就是right - left - 1。实现如下:
Java实现:
//方法 扩展中心
public int expandAroundCenter(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--;
right++;
}
return right - left - 1;
}
public String longestPalindrome_6(String s) {
if (s == null || s.length() < 1)
return "";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i); //奇数
int len2 = expandAroundCenter(s, i, i + 1);//偶数
int len = Math.max(len1, len2);
if (len > end - start) {
//重新计算start 和end
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
运行时间如下:
因为只识别回文序列,过滤掉了很大部分情况,虽然时间复杂度为o(n^2),但是执行效率更高。
时间复杂度:两个嵌套循环,最坏的情况下,O(n^2)
空间复杂度:O(1)
参考:
https://leetcode.com/problems/longest-palindromic-substring/solution/
http://windliang.cc/2018/08/05/leetCode-5-Longest-Palindromic-Substring/