罗德里格斯公式 理解、推导
罗德里格斯公式(Rodriguez formula)是计算机视觉中的一大经典公式,在描述相机位姿的过程中很常用。公式:
R = I + s i n ( θ ) K + ( 1 − c o s ( θ ) ) K 2 R = I + sin(\theta)K + (1 - cos(\theta))K^{2} R=I+sin(θ)K+(1−cos(θ))K2
在三维空间中,旋转矩阵 R R R可以对坐标系(基向量组)进行刚性的旋转变换。
R = [ r x x r x y r x z r y x r y y r y z r z x r z y r z z ] R = \begin{bmatrix} r_{xx} & r_{xy} & r_{xz}\\ r_{yx} & r_{yy} & r_{yz}\\ r_{zx} & r_{zy} & r_{zz} \end{bmatrix} R=⎣⎡rxxryxrzxrxyryyrzyrxzryzrzz⎦⎤
通常为了方便计算,基向量组中的向量是相互正交的且都为单位向量,那么 R R R就是一个标准正交矩阵。两个重要性质:
- R T R = R − 1 R = E R^{T}R = R^{-1}R = E RTR=R−1R=E
- ∣ R ∣ = 1 |R| = 1 ∣R∣=1
假设原坐标系基向量矩阵为 B B B,旋转后的坐标系基向量矩阵为 C C C。
B = [ b x b y b z ] = [ 1 0 0 0 1 0 0 0 1 ] B = \begin{bmatrix} b_{x} & b_{y} & b_{z} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} B=[bxbybz]=⎣⎡100010001⎦⎤
C = R B C = R B C=RB
其变换过程如图所示:
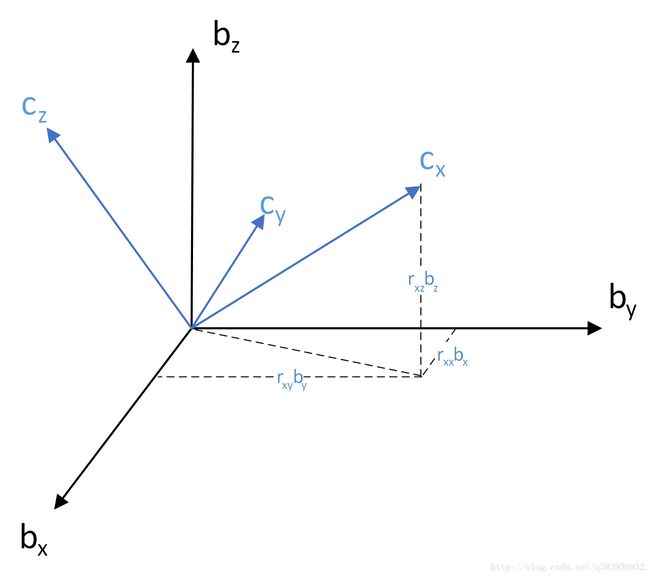
C = [ r x x r x y r x z r y x r y y r y z r z x r z y r z z ] [ b x b y b z ] C = \begin{bmatrix} r_{xx} & r_{xy} & r_{xz}\\ r_{yx} & r_{yy} & r_{yz}\\ r_{zx} & r_{zy} & r_{zz} \end{bmatrix}\begin{bmatrix} b_{x} & b_{y} & b_{z} \end{bmatrix} C=⎣⎡rxxryxrzxrxyryyrzyrxzryzrzz⎦⎤[bxbybz]
根据线性代数的定义,旋转矩阵 R R R就是从基向量矩阵 B B B到基向量矩阵 C C C的过渡矩阵。由于旋转矩阵 R R R是标准3阶正交矩阵,故旋转矩阵 R R R的自由度为3,这说明最少可以用三个变量来表示旋转矩阵 R R R,这就是**罗德里格斯公式(Rodriguez formula)**存在的基础。
**罗德里格斯公式(Rodriguez formula)**首先要确定一个三维的单位向量 k = [ k x k y k z ] T k = \begin{bmatrix} k_{x} & k_{y} & k_{z} \end{bmatrix}^T k=[kxkykz]T(两个自由度)和一个标量 θ \theta θ (一个自由度)。
**证明方法一:**
(图片摘自Wiki)
先考虑对一个向量作旋转,其中 v v v 是原向量,三维的单位向量 k = [ k x k y k z ] T k = \begin{bmatrix} k_{x} & k_{y} & k_{z} \end{bmatrix}^T k=[kxkykz]T是旋转轴, θ \theta θ 是旋转角度, v r o t v_{rot} vrot是旋转后的向量。
先通过点积得到 v v v 在 k k k 方向的平行分量 v ∥ v_{\parallel } v∥。
v ∥ = ( v ⋅ k ) k v_{\parallel } = (v \cdot k)k v∥=(v⋅k)k
再通过叉乘得到与 k k k 正交的两个向量 v ⊥ v_{\perp} v⊥ 和 w w w 。
v ⊥ = v − v ∥ = v − ( v ⋅ k ) k = − k × ( k × v ) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ( 1 ) v_{\perp} = v - v_{\parallel } = v - (v \cdot k)k = -k \times (k \times v) \cdot \cdot \cdot \cdot \cdot \cdot (1) v⊥=v−v∥=v−(v⋅k)k=−k×(k×v)⋅⋅⋅⋅⋅⋅(1) w = k × v w = k \times v w=k×v
这样,我们就得到了3个相互正交的向量。不难得出:
v r o t = v ∥ + c o s ( θ ) v ⊥ + s i n ( θ ) w v_{rot} = v_{\parallel } + cos(\theta)v_{\perp} + sin(\theta)w vrot=v∥+cos(θ)v⊥+sin(θ)w
再引入叉积矩阵的概念:记 K K K 为 k = [ k x k y k z ] T k = \begin{bmatrix} k_{x} & k_{y} & k_{z} \end{bmatrix}^T k=[kxkykz]T 的叉积矩阵。显然 K K K 是一个反对称矩阵。
K = [ 0 − k z k y k z 0 − k x − k y k x 0 ] K = \begin{bmatrix} 0 & -k_{z} & k_{y}\\ k_{z} & 0 & -k_{x}\\ -k_{y} & k_{x} &0 \end{bmatrix} K=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤
他有如下性质:
k × v = K v k \times v = K v k×v=Kv
为了利用该性质,需要将 $v_{rot} $ 代换为 $v $ 与 $k $ 的叉积关系,先根据(1)式做代换:
v ∥ = v + k × ( k × v ) v_{\parallel } = v+ k \times (k \times v) v∥=v+k×(k×v)
然后得到:
v r o t = v + k × ( k × v ) − c o s ( θ ) k × ( k × v ) + s i n ( θ ) k × v v_{rot} =v+ k \times (k \times v) - cos(\theta) k \times (k \times v) + sin(\theta)k \times v vrot=v+k×(k×v)−cos(θ)k×(k×v)+sin(θ)k×v
根据叉积矩阵性质:
v r o t = v + ( 1 − c o s ( θ ) ) K 2 v + s i n ( θ ) K v v_{rot} =v+ (1 - cos(\theta) )K^{2}v + sin(\theta)K v vrot=v+(1−cos(θ))K2v+sin(θ)Kv v r o t = ( I + ( 1 − c o s ( θ ) ) K 2 + s i n ( θ ) K ) v v_{rot} =(I+ (1 - cos(\theta) )K^{2} + sin(\theta)K )v vrot=(I+(1−cos(θ))K2+sin(θ)K)v
最后将 v 、 v r o t v、v_{rot} v、vrot 换为 B 、 C B、C B、C,就是罗德里格斯公式的标准形式。
B = ( I + ( 1 − c o s ( θ ) ) K 2 + s i n ( θ ) K ) C ⇔ R = I + ( 1 − c o s ( θ ) ) K 2 + s i n ( θ ) K B =(I+ (1 - cos(\theta) )K^{2} + sin(\theta)K )C \Leftrightarrow R = I+ (1 - cos(\theta) )K^{2} + sin(\theta)K B=(I+(1−cos(θ))K2+sin(θ)K)C⇔R=I+(1−cos(θ))K2+sin(θ)K
这里我取 k = [ 3 − 0.5 3 − 0.5 3 − 0.5 ] T k = \begin{bmatrix} 3^{-0.5} & 3^{-0.5} & 3^{-0.5} \end{bmatrix}^T k=[3−0.53−0.53−0.5]T ,可以看到通过罗德里格斯公式作基变换 C = R B C = R B C=RB的过程。
绘图用的Matlab代码:
在这里插入代码片
% Rodriguez formula
% 作者:龚冰剑
% 时间:2017年12月29日 16:39:14
clc
clear all
close all
%
W_vec = [3^(-0.5) 3^(-0.5) 3^(-0.5)];
W_mat = [0 -W_vec(3) W_vec(2);
W_vec(3) 0 -W_vec(1);
-W_vec(2) W_vec(1) 0 ];
%
zeta = 0 : pi / 180 : pi / 3;
%
origin_point = [0 0 0];
vector_x = [1 0 0];
vector_y = [0 1 0];
vector_z = [0 0 1];
% color
color_table = linspecer(length(zeta));
for i = 1 : length(zeta)
%hold off
plot3([origin_point(1) W_vec(1)],[origin_point(2) W_vec(2)],[origin_point(3) W_vec(3)], 'r--o', 'linewidth',2)
hold on
% 绘制原基向量
plot3([origin_point(1) vector_x(1)],[origin_point(2) vector_x(2)],[origin_point(3) vector_x(3)], 'r')
plot3([origin_point(1) vector_y(1)],[origin_point(2) vector_y(2)],[origin_point(3) vector_y(3)], 'r')
plot3([origin_point(1) vector_z(1)],[origin_point(2) vector_z(2)],[origin_point(3) vector_z(3)], 'r')
%
Rot_mat = diag([1 1 1]) + sin(zeta(i)) * W_mat + (1 - cos(zeta(i))) * W_mat * W_mat;
vector_x_Rot = vector_x * Rot_mat;
vector_y_Rot = vector_y * Rot_mat;
vector_z_Rot = vector_z * Rot_mat;
% 绘制变换后的基向量
plot3([origin_point(1) vector_x_Rot(1)],[origin_point(2) vector_x_Rot(2)],[origin_point(3) vector_x_Rot(3)], '-*','color', color_table(i, :))
plot3([origin_point(1) vector_y_Rot(1)],[origin_point(2) vector_y_Rot(2)],[origin_point(3) vector_y_Rot(3)], '-*','color', color_table(i, :))
plot3([origin_point(1) vector_z_Rot(1)],[origin_point(2) vector_z_Rot(2)],[origin_point(3) vector_z_Rot(3)], '-*','color', color_table(i, :))
axis([-0.5 1 -0.5 1 -0.5 1])
view(100, 30);
drawnow()
title(sprintf('θ = %.3f 度', zeta(i) * 180 / pi))
grid on
pause(0.05)
end
颜色表“linspecer.m”文件(推荐使用)
% function lineStyles = linspecer(N)
% This function creates an Nx3 array of N [R B G] colors
% These can be used to plot lots of lines with distinguishable and nice
% looking colors.
%
% lineStyles = linspecer(N); makes N colors for you to use: lineStyles(ii,:)
%
% colormap(linspecer); set your colormap to have easily distinguishable
% colors and a pleasing aesthetic
%
% lineStyles = linspecer(N,'qualitative'); forces the colors to all be distinguishable (up to 12)
% lineStyles = linspecer(N,'sequential'); forces the colors to vary along a spectrum
%
% % Examples demonstrating the colors.
%
% LINE COLORS
% N=6;
% X = linspace(0,pi*3,1000);
% Y = bsxfun(@(x,n)sin(x+2*n*pi/N), X.', 1:N);
% C = linspecer(N);
% axes('NextPlot','replacechildren', 'ColorOrder',C);
% plot(X,Y,'linewidth',5)
% ylim([-1.1 1.1]);
%
% SIMPLER LINE COLOR EXAMPLE
% N = 6; X = linspace(0,pi*3,1000);
% C = linspecer(N)
% hold off;
% for ii=1:N
% Y = sin(X+2*ii*pi/N);
% plot(X,Y,'color',C(ii,:),'linewidth',3);
% hold on;
% end
%
% COLORMAP EXAMPLE
% A = rand(15);
% figure; imagesc(A); % default colormap
% figure; imagesc(A); colormap(linspecer); % linspecer colormap
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% by Jonathan Lansey, March 2009-2013 �Lansey at gmail.com %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
%% credits and where the function came from
% The colors are largely taken from:
% http://colorbrewer2.org and Cynthia Brewer, Mark Harrower and The Pennsylvania State University
%
%
% She studied this from a phsychometric perspective and crafted the colors
% beautifully.
%
% I made choices from the many there to decide the nicest once for plotting
% lines in Matlab. I also made a small change to one of the colors I
% thought was a bit too bright. In addition some interpolation is going on
% for the sequential line styles.
%
%
%%
function lineStyles=linspecer(N,varargin)
if nargin==0 % return a colormap
lineStyles = linspecer(64);
% temp = [temp{:}];
% lineStyles = reshape(temp,3,255)';
return;
end
if N<=0 % its empty, nothing else to do here
lineStyles=[];
return;
end
% interperet varagin
qualFlag = 0;
if ~isempty(varargin)>0 % you set a parameter?
switch lower(varargin{1})
case {'qualitative','qua'}
if N>12 % go home, you just can't get this.
warning('qualitiative is not possible for greater than 12 items, please reconsider');
else
if N>9
warning(['Default may be nicer for ' num2str(N) ' for clearer colors use: whitebg(''black''); ']);
end
end
qualFlag = 1;
case {'sequential','seq'}
lineStyles = colorm(N);
return;
otherwise
warning(['parameter ''' varargin{1} ''' not recognized']);
end
end
% predefine some colormaps
set3 = colorBrew2mat({[141, 211, 199];[ 255, 237, 111];[ 190, 186, 218];[ 251, 128, 114];[ 128, 177, 211];[ 253, 180, 98];[ 179, 222, 105];[ 188, 128, 189];[ 217, 217, 217];[ 204, 235, 197];[ 252, 205, 229];[ 255, 255, 179]}');
set1JL = brighten(colorBrew2mat({[228, 26, 28];[ 55, 126, 184];[ 77, 175, 74];[ 255, 127, 0];[ 255, 237, 111]*.95;[ 166, 86, 40];[ 247, 129, 191];[ 153, 153, 153];[ 152, 78, 163]}'));
set1 = brighten(colorBrew2mat({[ 55, 126, 184]*.95;[228, 26, 28];[ 77, 175, 74];[ 255, 127, 0];[ 152, 78, 163]}),.8);
set3 = dim(set3,.93);
switch N
case 1
lineStyles = { [ 55, 126, 184]/255};
case {2, 3, 4, 5 }
lineStyles = set1(1:N);
case {6 , 7, 8, 9}
lineStyles = set1JL(1:N)';
case {10, 11, 12}
if qualFlag % force qualitative graphs
lineStyles = set3(1:N)';
else % 10 is a good number to start with the sequential ones.
lineStyles = cmap2linspecer(colorm(N));
end
otherwise % any old case where I need a quick job done.
lineStyles = cmap2linspecer(colorm(N));
end
lineStyles = cell2mat(lineStyles);
end
% extra functions
function varIn = colorBrew2mat(varIn)
for ii=1:length(varIn) % just divide by 255
varIn{ii}=varIn{ii}/255;
end
end
function varIn = brighten(varIn,varargin) % increase the brightness
if isempty(varargin),
frac = .9;
else
frac = varargin{1};
end
for ii=1:length(varIn)
varIn{ii}=varIn{ii}*frac+(1-frac);
end
end
function varIn = dim(varIn,f)
for ii=1:length(varIn)
varIn{ii} = f*varIn{ii};
end
end
function vOut = cmap2linspecer(vIn) % changes the format from a double array to a cell array with the right format
vOut = cell(size(vIn,1),1);
for ii=1:size(vIn,1)
vOut{ii} = vIn(ii,:);
end
end
%%
% colorm returns a colormap which is really good for creating informative
% heatmap style figures.
% No particular color stands out and it doesn't do too badly for colorblind people either.
% It works by interpolating the data from the
% 'spectral' setting on http://colorbrewer2.org/ set to 11 colors
% It is modified a little to make the brightest yellow a little less bright.
function cmap = colorm(varargin)
n = 100;
if ~isempty(varargin)
n = varargin{1};
end
if n==1
cmap = [0.2005 0.5593 0.7380];
return;
end
if n==2
cmap = [0.2005 0.5593 0.7380;
0.9684 0.4799 0.2723];
return;
end
frac=.95; % Slight modification from colorbrewer here to make the yellows in the center just a bit darker
cmapp = [158, 1, 66; 213, 62, 79; 244, 109, 67; 253, 174, 97; 254, 224, 139; 255*frac, 255*frac, 191*frac; 230, 245, 152; 171, 221, 164; 102, 194, 165; 50, 136, 189; 94, 79, 162];
x = linspace(1,n,size(cmapp,1));
xi = 1:n;
cmap = zeros(n,3);
for ii=1:3
cmap(:,ii) = pchip(x,cmapp(:,ii),xi);
end
cmap = flipud(cmap/255);
end
参考:
1.Rodrigues’ rotation formula - Wiki
2.《视觉SLAM十四讲》P49
3.关于罗德里格斯公式的简单推导 新浪博客
4.DERIVATION OF THE EULER–RODRIGUES FORMULA FOR THREE-DIMENSIONAL ROTATIONS…
