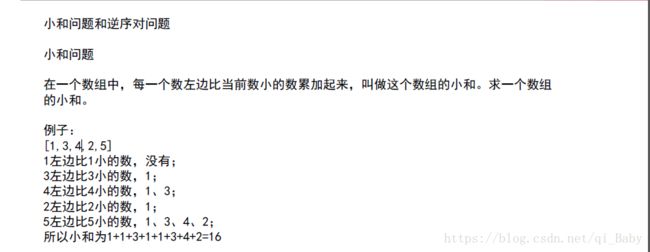
java 数组小和问题
看的牛客网左神的关于数组求小和问题,自己总结一下思路
如果第一次做的话,肯定是遍历求解,作为普通程序员第一眼就是这个思路,时间复杂度o(n*n)。哎!!
首先转变思路,其实这些都是套路,新手没办法,做多应该就会了。
比如1,我们求它在该数字中的所有小和,分别比它大的是,3 4 2 5 数字,1+1+1+1=4
3的小和,分别比它大的是 4 5 数字,3 +3=6
以此类推 4 , 2 , 5 数字小和分别为4,2,
以此思路正好符合归并排序,来解决这个问题,好吧我表达不好,粘贴别人的代码
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return mergeSort(arr, 0, arr.length - 1);
}
public static int mergeSort(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
//左侧部分的小和 + 右侧部分的小和 + 合并过程中的小和
return mergeSort(arr, l, mid) + mergeSort(arr, mid + 1, r) + merge(arr, l, mid, r);
}
public static int merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;//关键就是这个红色代码,其他的都是归并排序,其中(r-p2+1)表示在合并中,比如(1 3 4) 和(2 5)合并排序中,1 在(1 3 4)局部的小和已经 help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
return res;
}作为一个程序员,还是要脚踏实地理解这些东西,表达不好,更多是自己的理解然而表达不出来。坚持