fasttext做文本分类阶段性学习总结
fasttext做文本分类阶段性学习总结
- 预备知识
- logistic回归与softmax回归
- logistic回归
- sigmoid函数
- 决策边界
- 代价函数
- 正则化代价函数
- softmax回归
- 从二分类到多分类(one vs rest)
- softmax假设函数与代价函数
- logistic回归与softmax回归的关系
- 分层softmax (hierarchical softmax)
- 基本原理
- 层次之间的映射
- 模型的训练
- 神经网络结构
- 前向传播(输入->输出)
- 反向传播算法(BP)--学习权重矩阵
- fasttext源码分析
- 使用fasttext对文本进行分类
- 模型训练及测试
- 实验结果
- 参考
预备知识
logistic回归与softmax回归
logistic回归
logistic回归是一种有监督的统计学习方法,主要用于对样本进行分类。对于监督学习问题而言,常常会给定数据以及数据对应的标签值。比如我们可以通过logistic回归算法得到一个映射函数 f:X→y ,其中 X 为特征向量,X={x0,x1,x2,…,xn},y 为预测的结果。在逻辑回归这里,标签 y为一个离散值(y0,y1,y2,…,yn)。
sigmoid函数
如果希望分类器输出值在0和1之间: 0 ≤ h θ ( x ) ≤ 0 0≤h_{θ}(x)≤0 0≤hθ(x)≤0 ==> 引入 h θ ( x ) = g ( θ T x ) h_{θ}(x)=g(θ^{T}x) hθ(x)=g(θTx) ,其中: g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,则: h θ ( x ) = 1 1 + e − θ T x h_{θ}(x)=\frac{1}{1+e^{-θ^{T}x}} hθ(x)=1+e−θTx1
θ θ θ 为特征向量X={x0,x1,x2,…,xn}的参数,它是一个n维向量(在线性回归和logistic回归中, θ θ θ称参数,在神经网络中, θ θ θ称模型的权重)。
g ( z ) g(z) g(z)称为sigmoid函数(或称logistic函数),它的函数图像如下:
根据图像可知,sigmoid函数具有如下特点:
- 当z为0左右时,函数值为0.5左右
- z越大于0时,函数值越大于0.5越收敛于1
- z越小于0时,函数值越小于0.5越收敛于0
因此可以将sigmoid函数作为二分类问题的假设函数,将其转化为概率问题描述就变成了:
- 当 θ T x ≥ 0 θ^{T}x≥0 θTx≥0 时,样本标记的类型为某一类型的概率会等于或高于0.5,即: h θ ( x ) ≥ 0.5 h_{θ}(x)≥0.5 hθ(x)≥0.5 ==> 预测 y = 1 y=1 y=1
- 当 θ T x < 0 θ^{T}x<0 θTx<0 时,样本标记的类型为某一类型的概率会低于0.5,即: h θ ( x ) < 0.5 h_{θ}(x)<0.5 hθ(x)<0.5 ==> 预测 y = 0 y=0 y=0
则针对二分类问题而言: p ( y = 0 ∣ x ; θ ) + p ( y = 1 ∣ x ; θ ) = 1 p(y=0|x;θ)+p(y=1|x;θ)=1 p(y=0∣x;θ)+p(y=1∣x;θ)=1
决策边界
sigmoid函数 h θ ( x ) = g ( θ T x ) h_{θ}(x)=g(θ^{T}x) hθ(x)=g(θTx) 中,方程 θ T x = 0 θ^{T}x=0 θTx=0 表示决策边界,在二分类问题中,决策边界一边为A类,另一边划分为B类。如下例所示:
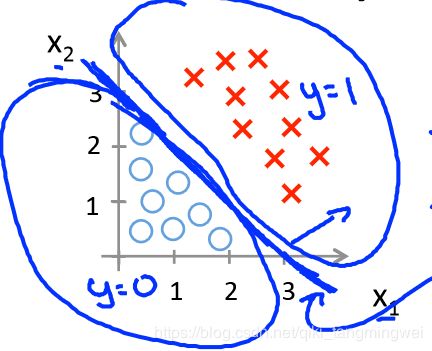
【例1】设 h θ ( x ) = g ( θ T x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_{θ}(x)=g(θ^{T}x)=g(θ_{0}+θ_{1}x_{1}+θ_{2}x_{2}) hθ(x)=g(θTx)=g(θ0+θ1x1+θ2x2) 其中 θ = ( − 3 1 1 ) θ=\begin{pmatrix}-3\\1 \\1\end{pmatrix} θ=⎝⎛−311⎠⎞
则: h θ ( x ) = g ( θ T x ) = g ( − 3 + x 1 + x 2 ) h_{θ}(x)=g(θ^{T}x)=g(-3+x_{1}+x_{2}) hθ(x)=g(θTx)=g(−3+x1+x2) , 当 θ T x = 0 θ^{T}x=0 θTx=0 时,即决策边界为: − 3 + x 1 + x 2 = 0 -3+x_{1}+x_{2}=0 −3+x1+x2=0,如下图所示:
图中加粗的蓝线即为 决策边界,可看出,在给定合适的 θ θ θ 参数前提下,模型能很好得对数据集做二分类。那么如何能自动得出合适的 θ θ θ 参数呢?可通过代价函数实现。
代价函数
代价函数又称“平方误差函数”,它是解决回归问题的常用手段,它通常是一个 凸函数(碗状)具有全局最优解(如正态函数)。
代价函数的功能就是用来拟合logistic回归模型参数 θ θ θ
对于sigmoid函数 g ( θ T x ) = 1 1 + e − θ T x g(θ^{T}x)=\frac{1}{1+e^{-θ^{T}x}} g(θTx)=1+e−θTx1, 需要为它找到一个代价函数 J ( θ ) J(θ) J(θ),使得 J ( θ ) J(θ) J(θ)为一个完整的凸函数,方便收敛以找到全局最优值(这里是最小值)。则定义: C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) y = 1 − l o g ( 1 − h θ ( x ) ) y = 0 Cost(h_{θ}(x),y)=\left\{ \begin{array}{rcl} -log(h_{θ}(x)) & & {y=1}\\ -log(1-h_{θ}(x)) & & {y=0}\\ \end{array} \right. Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))y=1y=0
函数曲线如下图所示:
- 【 i f if if y = 1 y=1 y=1 】 当 h θ ( x ) h_{θ}(x) hθ(x) -> 0 , C o s t Cost Cost -> ∞ ∞ ∞,则预测 p ( y = 1 ∣ x ; θ ) = 0 p(y=1|x;θ)=0 p(y=1∣x;θ)=0
- 【 i f if if y = 0 y=0 y=0 】 当 h θ ( x ) h_{θ}(x) hθ(x) -> 1 , C o s t Cost Cost -> ∞ ∞ ∞,则预测 p ( y = 0 ∣ x ; θ ) = 0 p(y=0|x;θ)=0 p(y=0∣x;θ)=0
合成一个表达式,则logistic回归代价函数表达式如下: C o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) Cost(h_{θ}(x),y)=-ylog(h_{θ}(x))-(1-y)log(1-h_{θ}(x)) Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
针对所有的m个标签数据集而言,则有:
J ( θ ) = − 1 m ∑ i = 1 m [ y i l o g ( h θ ( x i ) ) + ( 1 − y i l o g ( 1 − h θ ( x i ) ) ) ] J(θ)=-\frac{1}{m}\sum_{i=1}^{m}[y^{i}log(h_{θ}(x^{i}))+(1-y^{i}log(1-h_{θ}(x^{i})))] J(θ)=−m1i=1∑m[yilog(hθ(xi))+(1−yilog(1−hθ(xi)))]
正则化代价函数
当遇到特征参数很多,但是数据集较少等容易出现 过拟合(模型千方百计找到一个决策边界用以拟合训练数据,导致其无法泛化到其他新的样本中的现象)的情况时,解决方案分为两种:
- 减少 一些相关性较强的特征参数,缺点是容易丢掉一部分必要信息
- 保留所有变量,减少相关 θ i θ_{i} θi参数的值,即针对某些参数加入惩罚项(正则化)
正则化后的代价函数如下(m为样本个数,n为特征参数个数): J ( θ ) = [ − 1 m ∑ i = 1 m y i l o g ( h θ ( x i ) ) + ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(θ)=[-\frac{1}{m}\sum_{i=1}^{m}y^{i}log(h_{θ}(x^{i}))+(1-y^{i})log(1-h_{θ}(x^{i}))]+\frac{λ}{2m}\sum_{j=1}^{n}θ^{2}_{j} J(θ)=[−m1i=1∑myilog(hθ(xi))+(1−yi)log(1−hθ(xi))]+2mλj=1∑nθj2
对 ( θ 0 , θ 1 , θ 2 , . . . , θ n ) 加 惩 罚 项 , 防 止 相 关 项 过 大 导 致 过 拟 合 (θ_{0},θ_{1},θ_{2},...,θ_{n})加惩罚项,防止相关项过大导致过拟合 (θ0,θ1,θ2,...,θn)加惩罚项,防止相关项过大导致过拟合
接下来就可以使用梯度下降法(或其他更高级的算法如L-BFGS对代价函数求最优化解,直至收敛。
softmax回归
上面主要介绍了使用logistic回归做二分类,下面介绍的多分类思想也可用相似的思维方式来解决。
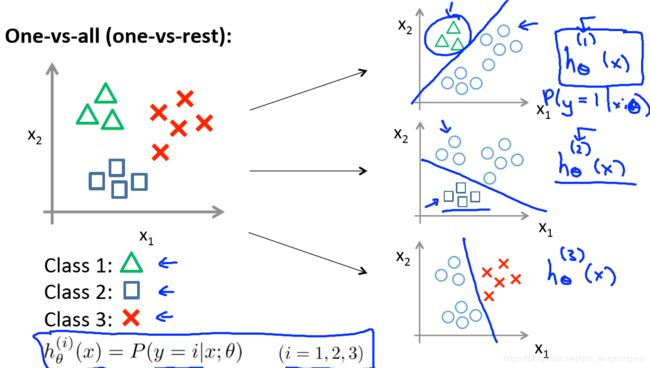
从二分类到多分类(one vs rest)
针对某一类型的概率,可以将一对一(二分类)扩展为一对多(one vs rest):
- 将类型class1看作正样本,其他类型全部看作负样本,然后我们就可以得到样本标记类型为该类型的概率p1;
- 然后再将另外类型class2看作正样本,其他类型全部看作负样本,同理得到p2;然后再将另外类型class2看作正样本,其他类型全部看作负样本,同理得到p2;
- 以此循环,我们可以得到该待预测样本的标记类型分别为类型class i时的概率pi,最后我们取pi中最大的那个概率对应的样本标记类型作为我们的待预测样本类型。
softmax假设函数与代价函数
在Softmax回归中,类标是大于2的,因此在我们的训练集 ( x 1 , y 1 ) , . . . , ( x m , y m ) {(x^{1},y^{1}),...,(x^{m},y^{m})} (x1,y1),...,(xm,ym)中的 y i ∈ ( 1 , 2 , . . . , K ) y^{i}∈{(1,2,...,K)} yi∈(1,2,...,K)。
给定一个测试输入x,我们的假设应该输出一个K维的向量,向量内每个元素的值表示x属于当前类别的概率。
假设函数如下:
h θ ( x ) = [ p ( y = 1 ∣ x ; θ ) p ( y = 2 ∣ x ; θ ) . . . p ( y = K ∣ x ; θ ) ] = 1 ∑ j = 1 K e θ ( j ) T x [ e θ ( 1 ) T e θ ( 2 ) T . . . e θ ( K ) T ] h_{θ}(x)= \left[ \begin{matrix} p(y=1|x;θ) \\ p(y=2|x;θ) \\ ...\\ p(y=K|x;θ) \end{matrix} \right] =\frac{1}{\sum_{j=1}^{K}e^{θ(j)^{T}x}}\left[\begin{matrix} e^{θ(1)^{T}} \\ e^{θ(2)^{T}} \\ ...\\ e^{θ(K)^{T}} \end{matrix} \right] hθ(x)=⎣⎢⎢⎡p(y=1∣x;θ)p(y=2∣x;θ)...p(y=K∣x;θ)⎦⎥⎥⎤=∑j=1Keθ(j)Tx1⎣⎢⎢⎡eθ(1)Teθ(2)T...eθ(K)T⎦⎥⎥⎤
代价函数如下
J ( θ ) = − [ ∑ i = 1 m ∑ k = 1 K 1 { y ( i ) = k } l o g e θ ( k ) T x i ∑ j = 1 K e θ ( j ) T x ( i ) ] J(θ)=-[{\sum_{i=1}^{m}\sum_{k=1}^{K}1{\{y^{(i)}=k\}log\frac{e^{θ(k)^{T}x^{i}}}{\sum_{j=1}^{K}e^{θ(j)^{T}x^{(i)}}}}}] J(θ)=−[i=1∑mk=1∑K1{y(i)=k}log∑j=1Keθ(j)Tx(i)eθ(k)Txi]
其中 1 { } 1\{\} 1{}是指示函数,即1=1,1=0
logistic回归与softmax回归的关系
下面是logistic回归代价函数的推导:
J ( θ ) = − [ ∑ i = 1 m y i l o g ( h θ ( x i ) ) + ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) ] = − [ ∑ i = 1 m ∑ k = 0 1 1 { y ( i ) = k } l o g p ( y ( i ) = k ∣ x ( i ) ; θ ) ] = − [ ∑ i = 1 m ∑ k = 0 1 1 { y ( i ) = k } l o g e θ ( k ) T x i ∑ j = 1 K e θ ( j ) T x ( i ) ] J(θ)=-[\sum_{i=1}^{m}y^{i}log(h_{θ}(x^{i}))+(1-y^{i})log(1-h_{θ}(x^{i}))] \\=-[{\sum_{i=1}^{m}\sum_{k=0}^{1}1{\{y^{(i)}=k\}logp(y^{(i)}=k|x^{(i)};θ)}}] \\=-[{\sum_{i=1}^{m}\sum_{k=0}^{1}1{\{y^{(i)}=k\}log\frac{e^{θ(k)^{T}x^{i}}}{\sum_{j=1}^{K}e^{θ(j)^{T}x^{(i)}}}}}] J(θ)=−[i=1∑myilog(hθ(xi))+(1−yi)log(1−hθ(xi))]=−[i=1∑mk=0∑11{y(i)=k}logp(y(i)=k∣x(i);θ)]=−[i=1∑mk=0∑11{y(i)=k}log∑j=1Keθ(j)Tx(i)eθ(k)Txi]
因此,可以说 Softmax回归是logisitic回归的推广,logistic回归是softmax回归在K=2时的特例。
分层softmax (hierarchical softmax)
标准的Softmax回归中,要计算 y = j y=j y=j 时的Softmax概率,我们需要对所有的K个概率做归一化,这在 ∣ y ∣ |y| ∣y∣很大时非常耗时。于是,分层Softmax诞生了,它的基本思想是使用树的层级结构替代扁平化的标准Softmax,使得在计算 y = j y=j y=j 时的Softmax概率时,只需计算一条路径上的所有节点的概率值,无需在意其它的节点。
基本原理
- 根据标签(label)和频率建立霍夫曼树;(label出现的频率越高,Huffman树的路径越短)
- Huffman树中每一叶子结点代表一个label;
- 采用了二元逻辑回归的方法,即规定沿着左子树走,那么就是负类(霍夫曼树编码1),沿着右子树走,那么就是正类(霍夫曼树编码0)。判别正类和负类的方法是使用sigmoid函数。
层次之间的映射
- 将输入层中的词和词组构成特征向量
- 将特征向量映射到隐藏层,隐藏层通过求解最大似然函数,然后根据每个类别的权重和模型参数构建Huffman树,将Huffman树作为输出。(参考:层次softmax函数(hierarchical softmax))
模型的训练
Huffman树中每一叶子结点代表一个label,在每一个非叶子节点处都需要作一次二分类,走左边的概率和走右边的概率,这里用logistic回归的公式表示:

神经网络结构
当样本规模很大时,仅采用单薄的logistic回归算法/softmax回归算法并不适用于处理n很大的场景,需借助神经网络结构。在本文介绍场景下的神经元是指带有logistic激活函数的人工神经元。神经网络一般分为三层,分别是输入层(input layer)、隐藏层(hidden layer)、输出层(output layer),在监督学习中,能看到输入和输出,而隐藏层的值在训练集里看不到,神经网络不止一个隐藏层。
前向传播(输入->输出)
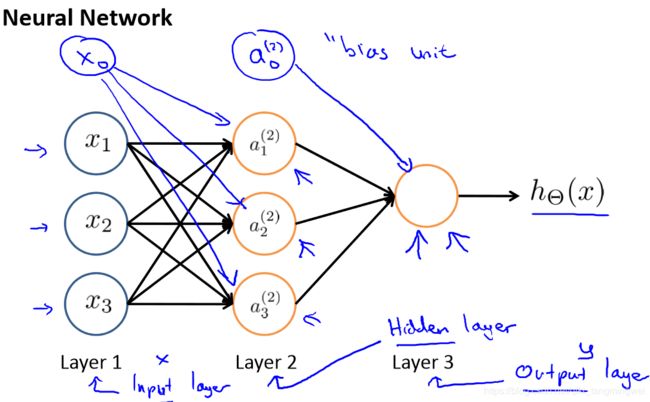
输入是如何计算而获得输出呢?先假设我们已经获得了权重矩阵 Θ Θ Θ(前文所述的各带有标签数据的x(i)对应的θ(i)参数),结合下图一种简单的神经元网络架构,对前向传播做个简单介绍。
图中:
- a i ( j ) a^{(j)}_{i} ai(j):第 j j j层第 i i i个神经元的激活项(由一个具体神经元计算输出的值)
- Θ ( j ) Θ^{(j)} Θ(j):权重矩阵,控制从某一层到另一层的映射
- x 0 x_{0} x0和 a 0 ( 2 ) a^{(2)}_{0} a0(2)为偏置单元,对于为什么会有偏置单元的设定本人理解为:对模型获得的决策边界作一定程度偏置的移动。理解可参考文章《神经网络中w,b参数的作用(为何需要偏置b的解释)》
则前向传播中,各激活项更新过程为:
前向传播是在获得权重矩阵 Θ Θ Θ的前提下,对输出模型函数,那么如何获取合适的权重矩阵参数呢?可通过反向传播算法实现。
反向传播算法(BP)–学习权重矩阵
【算法思想】在学习权重矩阵和过程中,我们首先 随机初始化权重矩阵 ( Θ ) (Θ) (Θ) ,然后feed训练样本到我们的模型,执行前向传播算法,对任意 x ( i ) x^{(i)} x(i)的值得到相应的 h Θ ( x ( i ) ) h_{Θ}(x^{(i)}) hΘ(x(i)),即得出输出值 y y y的向量,并观测我们期望输出 y y y和真实输出的误差。接着,我们计算误差关于权重矩阵的梯度,并在梯度的方向纠正它们。
【回顾】
回想一下logistic回归正则化的代价函数:
J ( θ ) = [ − 1 m ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(θ)=[-\frac{1}{m}\sum_{i=1}^{m}y^{(i)}log(h_{θ}(x^{(i)}))+(1-y^{(i)})log(1-h_{θ}(x^{(i)}))]+\frac{λ}{2m}\sum_{j=1}^{n}θ^{2}_{j} J(θ)=[−m1i=1∑my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
再回想一下,在神经网络中,可能有许多输出节点(如多分类)。我们把 h Θ ( x ) k h_{Θ}(x)_{k} hΘ(x)k表示为导致第k个输出的假设。我们的神经网络的代价函数将会是我们用于logisitc回归的一个综合泛化。神经网络的代价函数为:
J ( θ ) = [ − 1 m ∑ i = 1 m ∑ k = 1 K y k ( i ) l o g ( ( h θ ( x ( i ) ) ) k ) + ( 1 − y k ( i ) ) l o g ( 1 − ( h θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j , i ( l ) ) 2 J(θ)=[-\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{K}y^{(i)}_{k}log((h_{θ}(x^{(i)}))_{k})+(1-y^{(i)}_{k})log(1-(h_{θ}(x^{(i)}))_{k})]+\frac{λ}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s^{l}}\sum_{j=1}^{s^{l+1}}(Θ^{(l)}_{j,i})^{2} J(θ)=[−m1i=1∑mk=1∑Kyk(i)log((hθ(x(i)))k)+(1−yk(i))log(1−(hθ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θj,i(l))2
就像我们之前在logisitic回归中使用梯度下降所做的一样:
- 我们的目标是最小化代价函数: m i n Θ J ( Θ ) min_{Θ}J(Θ) minΘJ(Θ)
- 我们希望使用theta中的一组最优参数来最小化我们的成本函数 J J J
- 寻找最小的参数,需要使用梯度下降法,而梯度下降法最重要的是计算梯度 ∂ ∂ Θ i , j l J ( Θ ) \frac{∂}{∂Θ^{l}_{i,j}}J(Θ) ∂Θi,jl∂J(Θ) ,为了计算这个偏导数,我们使用反向传播算法
-
前向传播
a ( 1 ) = x a^{(1)}=x a(1)=x = > => => z 2 = Θ ( 1 ) × a ( 1 ) z^{2}=Θ^{(1)}×a^{(1)} z2=Θ(1)×a(1)
a ( 2 ) = g ( z ( 2 ) ) a^{(2)}=g(z^{(2)}) a(2)=g(z(2))(add a 0 ( 2 ) a^{(2)}_{0} a0(2)) = > => => z ( 3 ) = Θ ( 2 ) × a ( 2 ) z^{(3)}=Θ^{(2)}×a^{(2)} z(3)=Θ(2)×a(2)
a ( 3 ) = g ( z ( 3 ) ) a^{(3)}=g(z^{(3)}) a(3)=g(z(3))(add a 0 ( 3 ) a^{(3)}_{0} a0(3)) = > => => z ( 4 ) = Θ ( 3 ) × a ( 3 ) z^{(4)}=Θ^{(3)}×a^{(3)} z(4)=Θ(3)×a(3)
a ( 4 ) = g ( z ( 4 ) ) = h Θ ( x ) a^{(4)}=g(z^{(4)})=h_{Θ}(x) a(4)=g(z(4))=hΘ(x) -
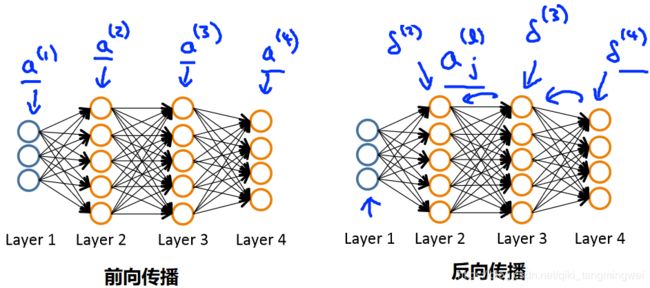
反向传播
- δ j l δ^{l}_{j} δjl :在第 l l l 层第 j j j 个神经节点激活值的误差
以第四层为例:
则在上图中, δ j ( 4 ) = a j ( 4 ) − y j = ( h θ ( x ) ) j − y j δ^{(4)}_{j}=a^{(4)}_{j}-y_{j}=(h_{θ}(x))_{j}-y_{j} δj(4)=aj(4)−yj=(hθ(x))j−yj
向量化表达: δ ( 4 ) = a ( 4 ) − y δ^{(4)}=a^{(4)}-y δ(4)=a(4)−y
第三层: δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) × g ′ ( z ( 3 ) ) = ( Θ ( 3 ) ) T δ ( 4 ) . ∗ a ( 3 ) . ∗ ( 1 − a ( 3 ) ) δ^{(3)}=(Θ^{(3)})^{T}δ^{(4)}×g^{'}(z^{(3)})=(Θ^{(3)})^{T}δ^{(4)}.*a^{(3)}.*(1-a^{(3)}) δ(3)=(Θ(3))Tδ(4)×g′(z(3))=(Θ(3))Tδ(4).∗a(3).∗(1−a(3))
第二层: δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) × g ′ ( z ( 2 ) ) = ( Θ ( 2 ) ) T δ ( 3 ) . ∗ a ( 2 ) . ∗ ( 1 − a ( 2 ) ) δ^{(2)}=(Θ^{(2)})^{T}δ^{(3)}×g^{'}(z^{(2)})=(Θ^{(2)})^{T}δ^{(3)}.*a^{(2)}.*(1-a^{(2)}) δ(2)=(Θ(2))Tδ(3)×g′(z(2))=(Θ(2))Tδ(3).∗a(2).∗(1−a(2))
则第 l l l层: δ ( l ) = ( Θ ( l ) ) T δ ( l + 1 ) . ∗ a ( l ) . ∗ ( 1 − a ( l ) ) δ^{(l)}=(Θ^{(l)})^{T}δ^{(l+1)}.*a^{(l)}.*(1-a^{(l)}) δ(l)=(Θ(l))Tδ(l+1).∗a(l).∗(1−a(l))
进一步,每个样本的误差合计: Δ i , j ( l ) : = Δ i , j ( l ) + a j ( l ) δ i ( l + 1 ) Δ^{(l)}_{i,j}:=Δ^{(l)}_{i,j}+a^{(l)}_{j}δ^{(l+1)}_{i} Δi,j(l):=Δi,j(l)+aj(l)δi(l+1)(其中, “ Δ ” “Δ” “Δ”是 “ δ ” “δ” “δ”的大写表示)
反向传播算法步骤
- 给定训练集 { ( x ( 1 ) , y ( 1 ) ) , . . . , x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),...,x^{(m)},y^{(m)})\} {(x(1),y(1)),...,x(m),y(m))}
- 初始化样本误差合计 Δ i , j ( l ) = 0 Δ^{(l)}_{i,j}=0 Δi,j(l)=0 (for all i i i j j j l l l)
- f o r for for i = 1 i=1 i=1 t o to to m : { m:\{ m:{
令: a ( 1 ) = x ( i ) a^{(1)}=x^{(i)} a(1)=x(i)
执行前向传播用来计算每一层的激活值: a ( l ) a^{(l)} a(l)( f o r for for l = 1 , 2 , . . . , L l=1,2,...,L l=1,2,...,L)
使用 y ( I ) y^{(I)} y(I)计算最后一层的误差 δ ( L ) = a ( L ) − y ( I ) δ^{(L)}=a^{(L)}-y^{(I)} δ(L)=a(L)−y(I)
反向计算: δ ( L − 1 ) δ^{(L-1)} δ(L−1), δ ( L − 2 ) δ^{(L-2)} δ(L−2),…, δ ( 2 ) δ^{(2)} δ(2) (使用公式: δ ( l ) = ( Θ ( l ) ) T δ ( l + 1 ) . ∗ a ( l ) . ∗ ( 1 − a ( l ) ) δ^{(l)}=(Θ^{(l)})^{T}δ^{(l+1)}.*a^{(l)}.*(1-a^{(l)}) δ(l)=(Θ(l))Tδ(l+1).∗a(l).∗(1−a(l)))
计算得到每层的样本误差合计: Δ i , j ( l ) : = Δ i , j ( l ) + a j ( l ) δ i ( l + 1 ) Δ^{(l)}_{i,j}:=Δ^{(l)}_{i,j}+a^{(l)}_{j}δ^{(l+1)}_{i} Δi,j(l):=Δi,j(l)+aj(l)δi(l+1) } \} } - 然后计算正则化: D i , j ( l ) : = 1 m ( Δ i , j ( l ) + λ Θ i , j ( l ) ) D^{(l)}_{i,j}:=\frac{1}{m}(Δ^{(l)}_{i,j}+λΘ^{(l)}_{i,j}) Di,j(l):=m1(Δi,j(l)+λΘi,j(l)) ( j ≠ 0 j≠0 j̸=0,即不含偏置单元)
D i , j ( l ) : = 1 m Δ i , j ( l ) D^{(l)}_{i,j}:=\frac{1}{m}Δ^{(l)}_{i,j} Di,j(l):=m1Δi,j(l) ( j = 0 j=0 j=0,偏置单元) - 误差-增量 矩阵D被用作累加器来累加误差,并最终计算得到我们所需要的偏导数: ∂ ∂ Θ i , j l J ( Θ ) = D i , j ( l ) \frac{∂}{∂Θ^{l}_{i,j}}J(Θ)=D^{(l)}_{i,j} ∂Θi,jl∂J(Θ)=Di,j(l)
fasttext源码分析
关于fasttext源码分析移步大神的github:fastText 源码分析
使用fasttext对文本进行分类
下面开始使用fasttext对文本做分类,考虑到实际项目的数据量实在是太庞大,而且本人参与的是一个关于多标签分类的项目,从阅读fasttext源码可知, fastText 的架构实际上只有支持一个 label,所以 它不太适合做多标签的分类(一条数据同时属于多个分类)。 虽然github上有issue提到可以通过更改数据label格式实现多分类,但经过尝试发现fasttext的多分类效果不是很理想 (PS:如果有好的建议,欢迎读者朋友留言指导^^)。但不可否认的是fasttext在处理单label分类还是非常棒的!
在这之后,笔者自己从网上下了些单标签的语料来训练模型,语料是来自清华大学的新闻文本。news_fasttext_train.txt
news_fasttext_test.txt
处理后的数据形式为词与词之间用空格分开,词语与标签默认用label分隔,如下图所示:

模型训练及测试
mport logging
import fasttext
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
classifier = fasttext.supervised("./news_fasttext_train.txt", "./fasttext-result.model", label_prefix="__label__")
result = classifier.test("./news_fasttext_test.txt")
print(result.precision)
print(result.recall)
精准率:0.923419980845
召回率:0.923419980845
由于fasttext貌似只提供全部结果的p值和r值,想要统计不同分类的结果,就需要自己写代码来实现了。
#-*- coding:utf-8 -*-
import logging
import fasttext
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
classifier = fasttext.load_model('./fasttext-result.model.bin', label_prefix='__label__',encoding='utf-8')
labels_right = []
texts = []
# ## 非多类别数据,一个数据只有一个label
with open('./news_fasttext_test.txt', 'r') as testfile:
for line in testfile:
line = line.rstrip()
#if(len(line.split("\t")[0])>2):
labels_right.append(line.split("\t")[1].replace("__label__", ""))
# predict 的时候,输入的是 list,每一个元素是一个要预测的实例;
texts.append(line.split("\t")[0])
#texts_file = open("./texts_file.txt","w+")
#print("=========print texts=============")
#print >> texts_file,texts
# 预测结果为二维形式,输出每一个类别的概率,按概率从大到小排序
labels_predict = [e[0] for e in classifier.predict(texts)] ##预测输出结果为二维形式
text_labels = list(set(labels_right))
text_predict_labels = list(set(labels_predict))
#text_labels_file = open("./text_labels_file.txt","w+")
print("=========text_labes==========")
print(text_labels)
#text_predict_labels_file = open("./text_predict_labels_file.txt","w+")
print("=========text_predict_labels=======")
print(text_predict_labels)
A = dict.fromkeys(text_labels, 0) # 预测正确的各个类的数目
B = dict.fromkeys(text_labels, 0) # 测试集中各个类的数目
C = dict.fromkeys(text_predict_labels, 0) # 预测结果中各个类的数目
for i in range(0, len(labels_right)):
B[labels_right[i]] += 1
C[labels_predict[i]] += 1
if labels_right[i] == labels_predict[i]:
A[labels_right[i]] += 1
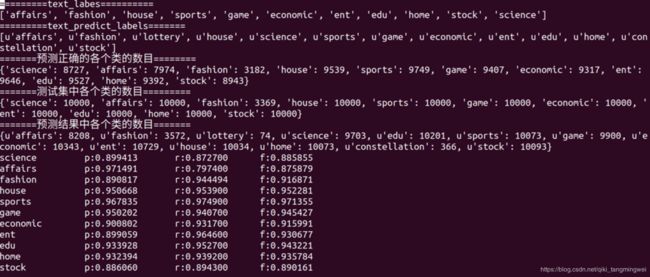
print("=======预测正确的各个类的数目========")
print(A)
print("=======测试集中各个类的数目=========")
print(B)
print("=======预测结果中各个类的数目=======")
print(C)
# 计算正确率,召回率,以及 F-score
for key in B:
try:
r = float(A[key]) / float(B[key])
p = float(A[key]) / float(C[key])
f = p * r * 2 / (p + r)
# 类别左对齐,占 15 个字符(为了美观)
print("%-15s p:%.6f\t r:%f\t f:%f" % (key, p, r, f))
except:
print("error:", key, "right:", A.get(key, 0), "real:", B.get(key, 0), "predict:", C.get(key,0))
实验结果
从结果上,看出fasttext的分类效果还是不错的,没有进行对fasttext的调参,结果都基本在90以上,多出了一个分类constellation的原因参看文档。文本分类(六):使用fastText对文本进行分类–小插曲
参考
- 吴恩达机器学习课程.
- fastText原理及实践(达观数据王江)
- 逻辑回归和softmax回归联系与区别.
- coursera-斯坦福-机器学习-吴恩达-第5周笔记-反向传播
- 层次softmax函数(hierarchical softmax)
- fastText 源码分析
- fasttext文本分类与原理
- 文本分类(六):使用fastText对文本进行分类–小插曲