三、基于MATLAB的数字图像处理————频率域滤波(一)
(三)基于MATLAB的数字图像处理————频率域滤波
一、二维离散傅里叶变换
令f(x,y)表示一幅大小为M*N像素的图像,其中x=0,1,2,…,M-1,y=0,1,2,…N-1。
由**F(u,v)*表示的二维离散傅里叶变换(DFT)为:
![]()
式中,u=0,1,2…,M-1,v=0,1,2,…,N-1。显然,F也是大小为MN的矩形区域,通常称为频率矩形。
离散傅里叶反变换(IDFT)的形式为:
![]()
式中,x=0,1,2,…,M-1和y=0,1,2,…,N-1。由 F(u,v) 可以得到 f(x,y)。
对于 f(x,y) 为实函数,他的 DFT 变换具有周期性:
![]()
他的 IDFT 也具有周期性:
![]()
令 R(u,v) 和 I(u,v) 分别表示 F(u,v) 的实部和虚部,则傅里叶谱定义为
![]()
变换的相角定义为
![]()
F(u,v) 还能表示为:
![]()
二、观察DFT的相关函数
在MATLAB中,一个图像数组的DFT可以用函数 fft2 得到
F=fft2(f)
若需要进行零填充,得到大小为P*Q的结果则有语法:
F=fft2(f,P,Q)
S=abs(F) %得到F的傅里叶谱
Fc=fftshift(F) %将变换的原点移动到频率矩形的中心
F=ifftshift(Fc) %将居中的结果反转
phi=angle(F) %得到DFT的相角
phi=atan2(imag(F),real(F)) %同样得到DFT的相角
F=S.*exp(i*phi) %由 给出的傅里叶谱和相角得到DFT
因为 fft2 把输入图像毫无缩放地变成了double类,但它值的范围仍然是 [0 255] 这样在进行图像显示时就会出错,我们定义 tofloat 函数将输入图像转化为范围为 [0 1] 内的浮点数,然后在过程的末尾用 tofloat 的 revertclass 特性将结果转换成与初始图像相同的类。代码如下:
function [out,revertclass]=tofloat(in)
identity=@(x) x;
tosingle=@im2single;
table={'uint8',tosingle,@im2uint8
'uint16',tosingle,@im2uint16
'int16',tosingle,@im2int16
'logical',tosingle,@logical
'double',identity,identity
'single',identity,identity};
classindex=find(strcmp(class(in),table(:,1)));
if isempty(classindex)
error('unsupported input image class.');
end
out=table{classindex,2}(in);
revertclass=table{classindex,3};
三、频率域滤波
1,基本原理
空间域滤波和频率域滤波的基础都是卷积,卷积定理表述为:空间域乘积的DFT为频域卷积;空间域卷积的DFT为频域内的乘积。
在进行滤波处理时我们经常用到的是后者:
![]()
令 H(u,v) 为滤波器传递函数,频域滤波的思想就是选择一个滤波器传递函数去对原图像的DFT进行处理(相乘),将结果再IDFT,得到的即为滤波之后的结果。
为了进行DFT运算,构造一个将大小为AD的f(x,y)和CD的h(x,y)构造成大小均为P*Q的扩展函数,要求
![]()
和
![]()
实现的函数代码:
function PQ=paddedsize(AB,CD,PARAM)
if nargin == 1
PQ=2*AB;
elseif nargin == 2 &&~ischar(CD) %CD为字符串返回真
PQ=AB+CO-1;
PQ=2*ceil(PQ/2); %ceil(x)返回大于等于x的最小整数
elseif nargin==2
m=max(AB);
p=2^nextpow2(2*m); %nextpow2(n)返回大于或等于n的绝对值的2的最小整数次幂
PQ=[P,P];
elseif (nargin==3) && strcmpi(PARAM,'pwr2')
m=max([AB CD]);
P=2^nextpow2(2*m);
PQ=[P,P];
else
error('wrong number of inputs.')
end
2,基本步骤
a,使用tofloat函数把输入图像转换为浮点图像
[f,revertclass]=tolfloat(f);
b,使用函数paddedzsize获得填充参数
PQ=paddedzsize;
c,得到的有填充图像的傅里叶变换
F=fft2(f,PQ(1),PQ(2));
d,生成一个大小为PQ(1)*PQ(2)的滤波器函数。(如果滤波器函数是居中的,则在使用滤波器之前要令H=ifftshift(H))。
e,用滤波器乘以该变换
G=H.*F;
f,获得G的IFFT:
g=ifft2(G);
g,将左上部的矩形修剪为原始大小:
g=g(1:size(f,1),1:size(f,2));
h,需要时,将滤波后的图像转换成原始输入图像的类:
g=revertclass(g);
3,用于频域滤波的M函数
假定滤波器函数的大小已被适当的调整,这时,我们将滤波后的图像转换成与输入想同的类,或者我们需要处理浮点型结果。定义一个M函数:
function g=dftfilt(f,H,classout)
[f,revertclass]=tofloat(f);
F=fft2(f,size(H,1),size(H,2));
g=ifft2(H.*F);
g=g(1:size(f,1),1:size(f,2));
if nargin==2||strcmp(classout,'original')
g=revertclass(g);
elseif strcmp(classout,'fltpoint')
return
else
error('undefined class for the output image')
end
4,从空间滤波器获得频率域滤波器
图像处理函数 freqz2可以实现从空间滤波器获得频率域滤波器的转换。
H=freqz2(h,R,C)
其中,h是一个二维空间滤波器,H是相应的二维频率滤波器。R是行数,C 是我们希望的滤波器的列数。通常,我们令R=PQ(1),C=PQ(2)。
做一个空间滤波和频率域滤波的比较
f=tofloat(f);
>> F=fft2(f);
>> S=fftshift(log(1+abs(F)));
>> imshow(S,[])
>> h=fspecial('sobel')
>h =
1 2 1
0 0 0
-1 -2 -1
>> PQ=paddedsize(size(f));
>> H=freqz2(h,PQ(1),PQ(2));
>> H1=ifftshift(H);
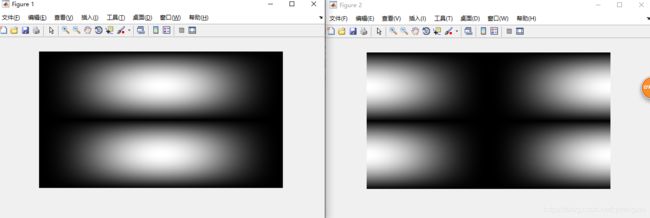
>> imshow(abs(H),[])
>> figure,imshow(abs(H1),[])
原始图像以及傅里叶谱为
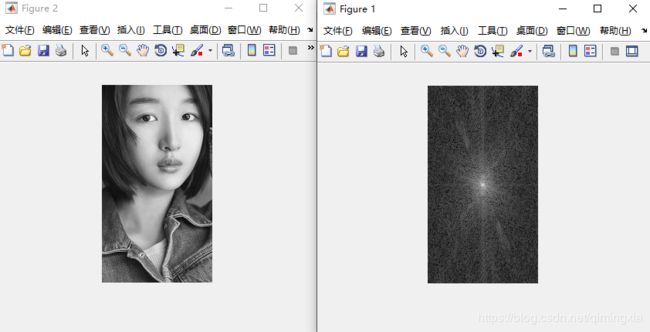
由空间滤波器得到的频率域滤波器的傅里叶谱及其ifftshift处理后的傅里叶谱
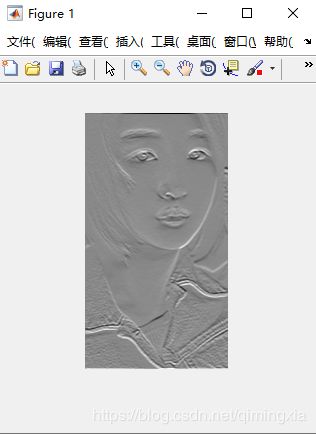
进行空间滤波
gs=imfilter(f,h);
imshow(gs,[])
gf=dftfilt(f,H1);
imshow(gf,[])
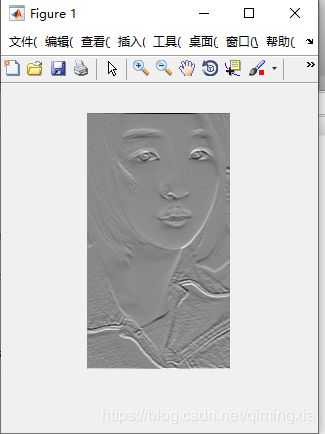
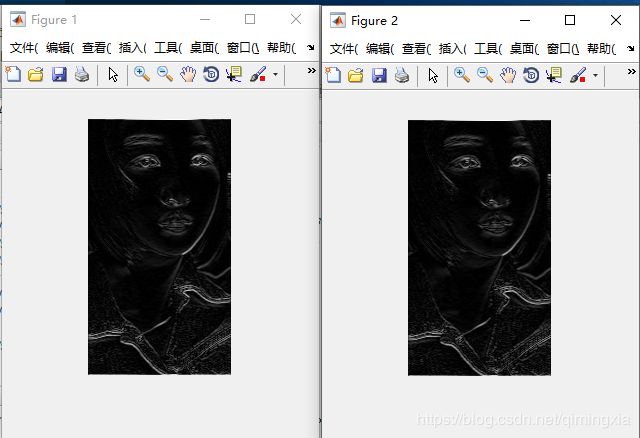
图像中的灰色调是由于gs和gf的负数值引起的,通过标定命令imshow,负数值会使得平均值增大。上面生成的Sobel模板h通过使用响应的绝对值来检测图像的水平边缘,更有意义。
imshow(abs(gs),[])
figure,imshow(abs(gf),[])
使用空间滤波和频率域滤波得到的图像所有实用目的是相同的,通过计算他们的差值,我们证明这一事实:
d=abs(gs-gf);
>> max(d(:))
ans =
single
8.0466e-07 %在这里 这个值的大小可以忽略不计。
>> min(d(:))
ans =
single
0
这个例子说明对于一幅图像的滤波,无论是选择空间滤波,还是选择这种空间滤波相应的频域滤波,最后得到的结果都是相同的。