博弈论总结
我只是个搬运工……
博弈论小结
by xaphoenix
写在前面
第一次写一个专题的总结,由于笔者水平有限,所以里面肯定会有很多不恰当之处,希望读者不吝赐教。此外,这个小结中,有大约2000字的直接复制粘贴的知识介绍,有几道题的题目分析或者题意概括来源于网上各位大牛的博客,所以笔者不具有著作权,具体的参考资料在本文最后列出。另外,为了节省页数(准备把这个带到现场),所以排版比较凌乱,字体基本都是五号字,仅仅是在标题处用加粗作为标记,希望读者能理解。本文几乎囊括了所有笔者知道的ACM中有关博弈论的知识内容,如有疏漏之处,希望能在csdn博客上私信我。例如本文由于笔者没有接触到关于纳什均衡和混合纳什均衡(WC2014上介绍过)相应的题目,所以没有深入的学习。例题部分包括了hdu、poj、zoj、bzoj中大多数经典的题目,当然主要的题目列表来源于cxlove的博弈论总结。笔者也会在之后的学习中不断添加例题。由于博弈论是一个需要经验和严谨证明的领域,所以希望能列出较为丰富的题目,能够从中学习掌握到大部分的博弈论知识和技巧。洋洋洒洒23000字,用时两周多完成,笔者也希望能借助此文,和更多对博弈论题目有兴趣的朋友相互交流、学习。
思路清晰的题目
例题 poj1678 I Love thisGame!
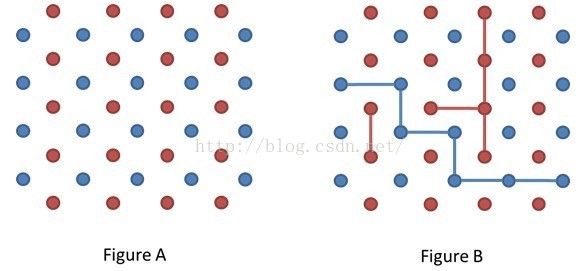
题意:给你一个有n个元素的集合。给定一个区间[a,b] (0 分析:很显然的动态规划思路。 例题 hdu3863 No Gambling 题意: 先手连接蓝色的点,从左向右要连出一个桥,如FigureB所示,后手连接红色的点,目的是不让先手完成任务,且红色边与蓝色边不能有任何接触。 分析:显然,先手必胜。先手的初始思路是沿一条不是底端直线的直线连过去,如果后手选择用两边的红点阻挡,显然先手可以选择连接出这条红边其下的一条蓝边。之后再把这些“脱离队伍”的边用纵向的蓝边连起来即可,因为这些边已有一个蓝点,所以后手无法占领或阻挡。 分析决策前后的不变量 (一)考虑奇偶性的变化 例题 hdu1079 Calendar Game 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1079 题意:从当前日期开始,玩家可以选择移动到下一天或者下一个月的同一天(如果月份加1超过12,则进入新的一年;如果移动使得新的日期不合法,则不能移动)。如果一个玩家移动到2001年11月4日,则该玩家胜利;如果一个玩家移动到2001年11月4日以后,则该玩家失败,问先手必胜还是后手必胜。 分析:我们发现,进行一次移动后,日期与月份之和的奇偶性总发生改变(除了9月30日和11月30日)。那么,如果不考虑这两天的情况下,如果初始日期月份与日期之和为偶数,则先手必胜。如果初始日期为9月30日或者11月30日,先手可以选择奇偶性不变的一次日期变化。这样就又成了先手必胜的情况。下面我们考虑是否中间会遇到这两个特殊点。如果初始状态为先手必胜,则先手总存在办法,不到达这个两个特殊点,即(8月30日和10月30日时不选择增加月份,9月29日和11月29日时不选择日期)。如果初始状态为先手必败,同样,后手总有办法不到达这两个特殊点。所以只可能在初始时除于这两个特殊点。即,读入日期后,我们判断日期与月份之和为偶数或为9月30日或为11月30日,先手必胜;否则,后手必胜。 例题 hdu1564 Play a game 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1564 题意:给你一个n*n的棋盘,游戏开始时有一块在拐角处的石子。两个玩家轮流移动该石子,移动时只能移动到相邻且未访问过的点,问先手必胜还是后手必胜。 分析:我们对该棋盘用1*2的长方形进行覆盖。若n为偶数,那么必存在一个覆盖方案。此时先手选择走向与当前状态同处一个长方形内的另一点。这样,无论先手怎么移动,先手必存在一种移动方法。由于这个游戏无平局,所以先手必胜。若n为奇数,我们考虑同样的方法,将n*n的棋盘除去起点的n*n-1格进行覆盖。之后无论先手怎么走,后手都存在一种移动方案,所以先手必败。 例题 hdu4203 Doubloon Game 题意:有n枚硬币,再给你一个数k,每次只能拿k^m枚(m为自然数),两人轮流拿,先拿完者胜。如果先手必败,输出0,否则输出先手保证必胜的情况下第一步最少拿的硬币数。 分析:先考虑k为奇数的情况,此时k的m次方一定为奇数。也就是说,如果n为奇数,那么最后一枚硬币一定是先手拿的,且第一轮只用拿1枚即可。若n为偶数,则先手必败。然后再考虑k为偶数的情况,首先我们可以手算出n=0,1,0,1,```,0,1,k。之后接下来用数学归纳法证明其周期为(k+1)。 例题 bzoj2927 多边形之战 题目:给定一个凸多边形的三角剖分,其中一个三角形被涂成了黑色,每次可以一刀割下一个三角形,割下黑色三角形的人胜利。 分析:建立其对偶图,问题转化为一颗树上有一个黑色节点,每次删去一个叶节点,删去黑色叶节点的人胜利。如果一开始黑色节点就是叶节点,那么先手必胜。其他情况,黑色点必须剩两个白点连在其旁边保证它不为叶节点,否则对方必胜。由于每次只能删去一个叶节点,这种情况下,胜负就只与n的奇偶性相关了。 例题 bzoj1443 游戏Game 题意:给定一个矩阵,一些位置由障碍,先手放置在某个位置,后手移动,先手再移动,一个格子只能经过一次,问是否先手必胜。 分析:在格子上移动,我们很容易想到黑白二染色。这样就转化为了经典的二分图博弈问题。接下来我们考虑移动的方法:对于任意一个点,如果存在一个最大匹配中这个点没有被匹配,则先手从这个点开始存在必胜策略。先手放置后,后手无论走到哪个点,先手一定能沿着匹配边走回去。如果不存在这样的一条边,说明找到了一条增广路,矛盾!所以一定存在匹配边。同理,当二分图存在完备匹配时,先手必败。题目还要求输出所有先手选择后必胜的点,枚举每个未匹配的点,沿着出边、匹配边、出边······这样的顺序深搜,深搜到的所有左侧的点就是左侧的可选点集。 (二)考虑总量的不变性 例题 hdu3544 Alice’s Game 题意:给n块的巧克力,每一块分别是xi*yi的,先手只能竖着切一刀,后手只能横着切一刀。谁不能切谁输,问先手是否有必胜策略。 分析:我们知道,如果一块巧克力被彻底切开,无论切的方式怎样,横切的总长度一定为(x-1)*y,竖切的总长度一定为x*(y-1)。而为了让对方切的次数变少,我们应该尽量让对方每次切的长度长,所以我们采用从中间切开的策略,使得对方每次切的都比较长。相应的,对方每次都选择切长度最小的。 对称构造 例题 hdu3951 Coin Game 题意:n个硬币围成一个圆,每次可以取连续的1~k个硬币,问先手是否有必胜策略。 分析:我们很容易能想到利用对称构造的思路来进行对抗。但是对称构造需要的是两个不相干且完全相同的子问题。本题是一个环,所以我们需要破环为两条相同长度的链。首先我们很容易发现,如果n<=k的话,先手可以一次取完。那么其他情况下,先手取完后会留下一条链。如果该链的长度为奇数,那么后手选取最中间的那一点即可,之后与先手进行对称构造;如果该链的长度为偶数,那么后手应该选取最中间的两点,但是注意k=1的情况需要特殊讨论,之后进行对称构造即可。 例题 poj2484 A Funny Game 题意:有N个硬币围成一圈,两个玩家轮流从中拿1个或者相邻的两个。先拿完者胜利,问是否先手必胜。 分析:如果n<2,显然先手必胜。如果n>=3,一定后手必胜:若n为偶数,则先手取完1个或两个后,后手选取同样的个数,所拿的硬币需要与先手拿的呈中心对称,这样就变成了两条完全相同的链,后手必胜。如果n为奇数,则先手取完1个或两个后,后手选取不同的个数,所拿的硬币同样需要与先手所拿的硬币呈中心对称。同样后手必胜。 从特殊情况入手 (一)从最简单的必胜态入手 例题 hdu1525Euclid’s Game 题意:给定两个正整数a,b。每次操作,可以将大的数减掉小的数的整数倍(减去后不能为负数)。如果一个操作者,将a,b中一个数变成0时游戏结束,并且该玩家胜利。求先手必胜还是后手必胜。 分析:不妨设a>=b,我们很容易发现,当a%b=0时,当前操作者必胜。如果a>=2*b时,当前操作者依然有必胜策略:如果a%b,b是必胜态,则先手将a,b变成a%b+b,b,这样后手只能将其变成a%b,b,然后先手必胜;如果a%b,b是必败态,则先手将a,b变成a%b,b,然后后手会输掉比赛。如果b 例题 poj1740 A New StoneGame / bzoj1982 Moving Pebbles 题意:有n堆石子,两个人轮流操作,每次操作分两步,第一步从某堆中去掉至少一个,第二步,可以把该堆剩余石子的一部分分给其它的某些堆(可省略)。问是否先手必胜。 分析:1堆显然是一个必胜点。考虑两堆的状况,双方的目的都是逼对方至两堆都是1的情况。如果一开始两堆的状况相同,那么后手可以模仿先手的做法,这样后手必胜。其他情况下,先手可以将两堆的情况传化为两堆相同,此时先手必胜。3堆时,先手可以通过对石子数最多的那一堆进行操作,使得情况传化为两堆相同的情况。此时先手必胜。猜想对于n堆石子,当且仅当n为偶数,且n对石子可以分成n/2对两两相同的堆时先手必败。对于必胜态:n为奇数时,选最大和最小的两堆,易知可以对最大堆操作,使得剩下的偶数堆两两相等。n为偶数且不满足n/2对两两相同时,根据同样的做法,同样可以转移到必败态上。对于必败态:无论取哪堆都不能使得剩下的石子变成n/2对两两相同的状态。 (二)从最简单的必败态入手 例题 hdu2147 kiki’s game 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2147 题意:在一个n*m的矩阵中起始位置(1,m),走到终止位置(n,1);游戏规则是只能向左,向下,左下方向走,想走到终点的为获胜者。 分析:最容易想到的必败态就是1*1的矩阵,此时先手必败。那么1*2,2*1,2*2都为先手必胜。假设先手当且仅当面对n和m全为奇数的矩阵时必败,利用数学归纳进行考虑。如果当前状态为两偶,则其沿对角线走,对手面对的将是两奇,此时先手必胜;如果当前状态为一奇一偶,则其沿偶的那个方向走,对手面对的仍然是两奇,此时先手必胜;如果当前状态为两奇,无论其怎么走,也不能给对手留下两奇的状态,此时先手必败。 (三)从固定参数的情况进行讨论 例题 hdu1538 A Puzzle forPirates 题意:有n个海盗,分m块金子,其中他们会按一定的顺序提出自己的分配方案,如果50%以上的人赞成,则方案通过,开始分金子,如果不通过,则把提出方案的扔到海里,下一个人继续。 分析:经典的海盗分金问题。看了cxlove大神的博客才会的。我们先考虑n<=2*m的情况:如果只有1号和2号,那么根据50%的规则,无论2号提出什么条件都能通过,所以2号可以100:0分配。如果有1号2号3号三人,3号为了获得1号的支持,只用给1号一枚金币即可,剩下金币都给自己。同理,4号存在时,会贿赂2号一枚金币,剩下全留给自己。5号存在时会贿赂1号3号各一枚金币,其余留给自己。以此类推。如果n=2*m+1:那么n号海盗为了让其他人支持来保命,会选择把m个金币,给前面2m个人中的m个人,这样就能获得50%以上的支持。下来考虑n>2*m+1的情况。首先,第2*m+1号人的做法同上,第2*m+2号人为了获得支持,将给第2*m+1号人的分配方案中没分配到的m个人金币,这样就能拥有50%的支持。第2*m+3号人无法获得支持,所以他提出的方案一定无法通过,只能选择支持后面的人。2*m+4号有了前2*m个人中m个人的支持,和2*m+3号的支持,他的方案也能通过。第2*m+4、2*m+5、2*m+6、2*m+7同样获得不了足够的支持,而2*m+8的人拥有了50%的支持率,他的方案可以通过。以此类推。我们可以发现,2*m+2^k号海盗的方案可以通过,处在这样两个特殊海盗中间的其他海盗的方案无法通过。 (四)分析参数之间的大小关系 例题 bzoj4147 Euclidean Nim 题意:Euclid和Pythagoras在玩取石子游戏,一开始有n颗石子。Euclid为先手,他们按如下规则轮流操作:若为Euclid操作,如果n 分析:首先我们会发现,如果p和q有最大公约数d,那么当n不是d的倍数时,游戏永远不会停止,反之,我们可以把这个公约数消去,使得p和q互质,并且这种情况下,游戏一定能结束。下面我们分情况讨论: 1、p=q。此时p只能为1,则先手必胜。 2、p>q,n 3、p>q,n>=p。如果先手操作后x>=q,那么后手可以将石子数变成xmod q,就转化为了状态2,先手必败。所以先手只能取成n mod p,然后后手+q,先手-p,这样不停进行下去。所以当(p-q)|(n mod p)且n mod p>q 时先手必胜。 4、若p 5、若p 博弈树 (一)博弈树基础 用搜索去处理一个点的后继状态,如果后继态中有一个必败态,则该点为必胜态,否则为必败态。 例题 hdu1760 A New TetrisGame 题意:给定一个n*m的棋盘(n,m<=50),棋盘的每一格用0,1表示,0表示未占用,1表示已占用,其中0的个数不超过40。现在两个玩家,轮流放置一个2*2的俄罗斯方块,放置的方块之间不能有重叠,且不能放到已占用的格子上。问是否先手必胜。 分析:由于0的个数很少,我们可以用搜索进行递归处理,在每一层中,遍历整个棋盘,枚举放下2*2俄罗斯方块的位置。返回值为0或1,当且仅当后继状态有一个返回值为0时返回1,其他情况返回0。 例题 hdu4155 The Game of 31 题意:有24张牌,最多由4张1,2,3,4,5,6组成。两个玩家轮流选一张牌,总的牌的点数不能超过31,谁不能选牌谁输。 分析:dfs求解即可。 例题 bzoj3404 Cow Digit Game又见数字游戏 题意:给你一个数,两个玩家轮流操作,可以给原数减去一个原数各个位上最大的数字,也可以给原数减去一个原数各个位上最小的非0数。问是否先手必胜。 分析:暴力求PN表即可。 例题poj2068 Nim 题意:有2n个人,两方各n个人,交叉坐,每个人可以取的石子有一个最大限制,总共有S颗石子,哪一方取了最后一颗石子就输了,问是否先手必胜。 分析:记忆化搜索求PN态即可。 (二)简单优化 例题 zoj2686 Cycle Game 题意:N个点形成一个环,相邻点之间有权值。从0号点开始,可以选择往两边移动,前提是权值为正,移动之后,可以将权值减少一个任意的正数。最后无法移动者输,问是否先手必胜。 分析:对搜索进行优化。我们发现,如果有一个方向上有连续的奇数个非0数,那么先手可以将权值降为0,后手就无法返回了,如果后手也将权值降为0,则最终先手必胜,反之,如果后手不降为0,那么先手返回一步,将权值降为0,出现两边都是0的情况,后手无法移动,此时先手必胜。在这个优化下可以搜索出答案。 例题 zoj3057 Beans Game 题意:有三堆石子,每堆石子的个数都不超过300,两个玩家轮流操作,每次可以从一堆石子拿任意多石子,也可以从两堆石子拿任意多相同的石子。问是否先手必胜。 分析:同样思路是求PN态,但是数据比较大,所以我们需要用dp来递推。 例题 zoj1039 Number Game 题意:我们在2-20这19个数字上进行游戏。两个玩家轮流取数,取完这个数后,这个数的倍数不能再取,而且某两个不能取的和,也不能再取。 分析:利用状压dp来表示每个数字是否被选,然后暴力求pn表即可。 (三)极大极小搜索和alpha-beta剪枝 极大极小搜索:利用估价函数,考虑每一步行动后对先手的价值。那么每次先手搜索时,都会从估价最高的行动策略开始搜索。相应地,每次后手搜索时,都会从估价最低的行动策略开始搜索。 alpha_beta剪枝:alpha记录的是博弈树搜索到当前深度时的最大估价值,也就是最好的情况。beta记录的是博弈树搜索到当前深度时最小的估价值,最坏的情况,利用这两个信息进行剪枝,使得搜索加快。 例题 poj1085 Triangle War 题意:给出10个点,总共18条边,两个玩家轮流加入一条边,如果形成一个三角形,则三角形归当前玩家所有,并且可以额外再走一步。最后三角形多的人获胜,问是否先手必胜。 分析:构建估价函数,利用极大极小搜索和alpha-beta剪枝来优化博弈树搜索。 经典博弈问题及其拓展问题 (一)巴什博奕(BashGame) 游戏情形:n个物品组成一堆,两个人轮流从这堆物品中取物,规定每次至少取一个,最多取m个,最后取尽物体一方赢。 对抗策略分析:考虑n对m+1取模的余数。如果为0,那么如果先手取k个(0 例题 hdu1846 Play a game /hdu2188 悼念512汶川大地震遇难同胞——选拔志愿者 / hdu2149 Public Sale 题意/分析:巴什博奕原型 例题 poj2368 Buttons 题目链接:http://poj.org/problem?id=2368 题意:有一堆物品,给你物品的个数k,让你找出最小的那个L(每个玩家最多取的物品的个数),使得先手必败,如果不能则输出0。 分析:根据巴什博奕,我们需要找出一个最小的L使得k%(L+1)=0,暴力找出k的所有因数即可。 例题 hdu1847 Good Luck inCET-4 Everybody! 题意:n张牌,两位玩家每次能抓取的牌数为2的自然数次幂。问先手必胜还是后手必胜。 分析:注意到2的幂中包含1和2两个,我们可以考虑n模3的情况。如果n%3=0,则后手总有办法保持n%3=0这个状态,先手必败。如果n%3!=0,则先手总有办法将当前状态转移为n%3!=0上,先手必胜。 例题 hdu2897 邂逅明下 题意:n个硬币,两人轮流取,最少取p个,最多取q个。最后取的人输,问是否先手必胜。 分析:我们利用巴什博奕的思路,将n化成(p+q)*k+r的形式。如果r==0,那么先手取q个,若后手取x,先手则取p+q-x,这样最后给后手留下p个硬币,必须一次取完,此时先手必胜;如果0 例题 hdu1517 AMultiplication Game 题意:初始p=1,两位玩家轮流,给p乘上一个2到9的数,谁先使得p超过给定的n谁胜利。 分析:如果刚开始的数时位于2-9之间的,那么先手必胜。如果刚开始的数时位于10-18的,那么先手必败,因为无论先手选什么,后手只要乘以2就能够到达10-18之内的所有数。如果刚开始的数位于19-162,那么先手必胜,可以这么想,先手选一个9,那么后手乘以一个数后,Num>=18,此时先手再乘以9,那么就大于162之内的任何数了。如果刚开始的数位于163-324时,那么先手必败,可以这么考虑,后手可以控制一个数到达9-18之间,那么先手如果乘个2的话(乘以大的那就更不用说了),那么就会到达18-36这个区间,此时后手再乘以9,那么就可到达163-324之间的任何数。以此类推,不断除2、除9循环,找到其所在区间即可。 (二)威佐夫博弈(Wythoff Game) 游戏情形:有两堆数量各若干的物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取尽物体一方赢。 对抗策略分析:我们用(ak,bk)(ak<=bk,k=0,1,2,···,n)表示两堆物品的数量并称其为局势。如果甲面对(0,0),那么甲已经输了,这样的局势我们称为奇异局势。前几个奇异局势为:(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。可以看出,a0=b0=0,ak是未在前面出现过的最小的自然数,而bk=ak+k。奇异局势有如下三个性质: 【性质1】 任何自然数都包含在一个且仅有一个奇异局势中。 【性质2】 任意操作都可以将奇异局势变为非奇异局势 【性质3】 采用适当的方法,可以将非奇异局势变为奇异局势 分析:假设面对的局势是(a,b)。 如果b=a,则同时从两堆中取走a个物体,就变成了奇异局势(0,0)。 如果a=ak,b>bk,则取走b-bk个物体,则变为奇异局势。 如果a=ak,b 如果a>ak,b=ak+k,则从第一堆中拿走多余的数量a-ak即可。 如果a a=aj(j ‚a=bj(j 从上述分析得知,两个人如果都采用正确操作,那么面对非奇异局势,先拿者必胜;反之,则后拿着必胜。 我们如何判断一个局势是否为奇异局势? 公式: 则我们可以先求出。若,那么,。若,那么,。若都不是,那么就不是奇异局势。 或者我们判断a是否等于 例题poj1067 取石子游戏 / hdu1527 取石子游戏 题意/分析:威佐夫博弈原型 例题hdu2177 取(2堆)石子游戏 题意/分析:威佐夫博弈原型,要求输出第一步 (三)尼姆博奕(NimmGame) 游戏情形1:有N堆物品,其中第i堆有Pi个物品,每次从某一堆里选出若干物品去掉(但不能不取)。两人轮流取物,谁不能继续取就输了。该问题称为Nim问题。 游戏情形2:有N堆物品,其中第i堆有Pi个物品,每次从某一堆里选出若干物品去掉(但不能不取)。两人轮流取物,谁不能继续取就赢了。该问题称为Anti-Nim问题。 对抗策略分析1:假设某个初始局面为先手必胜,那么先手每一步都必须使对手落在必败点,因此,对于每个局面,要么为胜局面,要么为负局面。我们用非0表示胜局面,用0表示负局面。对于某一个局面,若为非0局面,它的任务就是要寻找某一种取法,使局面变为0局面。即他的对手无论怎么取,都会使局面又变成0局面。那么这种对弈又有什么规律呢? 【定理】如果一个局面先手必胜,就称之为N局面,反之称之为P局面。对于一个局面,令。若S=0,则为P局面,否则为N局面。 证明:1)当时,S=0,为P局面,满足条件。 2)当S=0,即。若取堆i中的物品,使得堆i中的物品发生变化,显然它的子局面P的异或和不为0,即为N局面。 3)当S<>0,设S的二进制位是A1···An,考虑第一位是1的情况。在P中取出该位同是1的局面不妨设为P1。可知,令,可知,即N局面至少存在一个子局面是P局面。 例题 poj2234 Matches Game /hdu1849 Rabbit and Grass 题意/分析:尼姆博奕原型 例题 poj2975 Nim / hdu1850Being a Good Boy in Spring Festival / hdu2176 取(m堆)石子游戏 题意:有n堆石子,两人轮流从任一堆中取任意个石子(至少一个),最后一个取石子的人为赢家。题目给出了如何判断当前形势为必胜态的方法。问最后有多少种赢法。 分析:首先求n堆石子数异或后的结果t。如果t=0,则为必败态。否则,我们可以使它变成必败态然后让对手决策。由于双方都是最优策略,第一步决定后,以后的决策也就定了。所以有多少种赢法取决于第一步可以创造多少必败态。我们只要枚举每堆石子的个数,判断有多少组t^a[i] 例题 hdu1730 Northcott Game 题意:在一个n行m列的棋盘上进行一个游戏:每行都有一黑一白两棋子,先手只能移动黑色棋子,后者只能移动白色棋子。每次移动时,都可以将自己的一个棋子移动到同一行的任意位置,但是移动的过程中不能穿过对方的棋子。问是否先手必胜。 分析:首先我们很容易发现,n行的游戏是互不干扰的,此外,我们发现,每一行的游戏情况和取石子是同样的。把每一行两个棋子之间的距离-1作为每一堆的石子个数进行nim游戏,和这个游戏是完全等价的。现在我们考虑为什么对于一行移动棋子等价于取石子。如果A要取k个石子,即要缩短两个棋子之间k的距离,如果B不愿意这样修改,一定会沿反方向移动他的棋子,那么A可以沿B移动的方向移动自己的棋子,始终保持同样的距离。由于棋盘有边界,所以总有一刻B无法这样做。经过这样的变换,题目中描述的游戏就完全等价于Nim游戏了。 例题 zoj3529 A Game BetweenAlice and Bob 题意:给你n个数ai(ai<=5000000),两个玩家轮流操作,可以将其中一个数换成一个非自己的因数。问是否先手必胜。 分析:很容易发现,将一个数替换成一个因数,相当于从原数中去掉几个质因子,所以我们只需要知道每个数的质因子个数,就可以转化成经典的Nim游戏模型了。 例题 zoj3591 Nim 题意:根据题目给出的代码,构造出a数组,问多少种方案使得,将a数组中连续的一段作为Nim游戏每个堆的石子数,先手必胜。 分析:我们考虑先手必败的个数:我们求出a[i]的前缀异或和,我们只要知道在新的a数组中有多少对a[i]、a[j]相等即可,这里我们可以用map简单的维护下。同时还要减去新的a数组中a[i]=0的个数。 例题 bzoj2819 Nim 题意:给定一个棵树,每个节点是一堆石子,给定两种操作:1、改变x号节点的石子数量;2、用从x到y的路径上的所有堆石子玩一次Nim游戏,询问先手是否有必胜策略。 分析:简单的Nim游戏,不过需要用树链剖分来维护下,需要支持单点修改和区间查询。 例题 bzoj3759 Hungergame 题意:给定n个箱子(n<=20),每个箱子里有一些石子,两个人轮流操作,每个人可以进行以下操作之一:1.打开任意多的箱子2.从一个打开的箱子中拿走任意多的石子。不能操作者输,问是否先手必胜。 分析:先给出结论:先手必胜当且仅当给出的数字集合存在一个异或和为零的非空子集,则先手必胜。先证这样一个必败态:当前所有打开的箱子中的石子数异或和为零,且所有关闭的箱子中的石子数的集合中不存在一个异或和为零的非空子集。当前玩家有两种操作,第一种是从一个打开的箱子中拿走一些石子,那么对方可以按照Nim游戏的玩法,使得状态再次回到这种情况上。第二种是打开一些箱子,由于剩下的部分不存在异或和为0的子集,所以当前状态下的异或和必不为0.那么对方同样可以通过操作使得状态回到这种情况上。所以,如果初始状态下,不存在一个异或和为零的子集,先手必败,否则先手必胜。下来我们考虑如何求是否存在这样的子集。由于n很小,我们可以用meetin the middle的方法,将之前得到的装填存在一个map里,不过要注意特判两边什么都不选的这种特殊情况。 对抗策略分析2: 所有物品的数目都为1:显然,若有偶数堆物品堆,则必胜,否则必败。 ‚如果恰好只有一堆物品数目大于1。我们可以把这堆物品取完或取得只剩下1,使得只剩下奇数堆数目为1的物品留给对方,由情况可知,必胜。 ƒ如果有至少两堆物品的数目大于1。考虑异或值:若异或值不为0,则按照Nim走法取石,这样,当对手某次取完物品后,肯定会出现情况‚,必胜。 证明:按照Nim走法,则取完物品后,必定会给对手留下异或值为0的局面,因此不可能给对手留下情况‚的局面,而对手一次最多将一堆物品数大于1的物品堆处理掉。因此情况‚肯定会出现。 例题 zoj2507 Let’s play agame / hdu1907 John / poj3480 John / hdu2509 Be the Winner / bzoj1022 小约翰的游戏John 题意/分析:Anti-Nim原型 (四)巴什博奕的扩展——k倍动态减法游戏 游戏情形:有一个整数S(>=2),先行者在S上减掉一个数x,至少是1,但小于S。之后双方轮流把S减掉一个正整数,但都不能超过先前一回合对方减掉的数的k倍,减到0的一方获胜。问:谁有必胜策略。具有该问题背景的游戏称为k倍动态减法游戏。 对抗策略分析:曹钦翔的《从“k倍动态减法游戏”出发探究一类组合游戏问题》中提到了动态规划的优化算法。这里不再累述。这里介绍下另一种纯数学方法: 1. k=1的情况 我们将石子数n转化为二进制下的表示,那么,先拿者拿走最后一个1,后者一定拿不到比他高的1,那么先拿者一定会赢。当然,如果n最初为2的j次方,那么先拿者当然不能拿走唯一的1,此时先拿者必输,因为无论怎么拿,新的局面将成为之前所述,后拿者拥有了必胜策略。 2.k=2的情况 此时博弈也称为FIB博弈。我们知道任何一个非斐波那契数n都可以写为多个两两不相邻的斐波那契数的和(其中大的那个数必然大于小的那个数的2倍),这样的话,先取者A先拿走一个小的斐波那契数x,那后取者就无法取到另一个较大的斐波那契数y,这样又给A留下了一个斐波那契数,一直递归下去,A一定就是赢着。但是,如果A最初面临的就是一个斐波那契数Fn,而Fn只能写为Fn-1+Fn-2,如果取Fn-2,由于Fn-1<2*Fn-2,所以B可以取完;如果取其他任意一个非斐波那契数m,B得到的剩下的数Fn-m就相当于上面A最初面临的n,即B必胜。 3. k的一般情况 按照之前的思路我们的目的就是要让n写为的形式,而且两两相邻之间的倍数关系应该大于k。这样,先拿者A取走小一点的数n1,后拿者B必然不能取走n2。这样的话,B自然不能取完,所以A获胜。 在解题时,我们应该求出某个数列a[],这个数列要求任何一个不在这个数列里面的数都可以用这个数列里多项的和表示,但须满足前一项的k倍小于后一项的前提条件。为了求出这个数组a,我们引入另一个数组b[],b[i]表示a[0],a[1],a[2],···,a[i]可以找到两项a[x]和a[y]满足a[x]*k 接下来的问题就是要解决先拿者第一回合应取走的最小石头数:先从n里减去小于n的最大的a[i],然后递归求这个剩下的n里最大的a[k],n=n-a[k],递归过程一直进行到n=0为止。最后被减去的a[k]即为问题的解。 例题 hdu2516 取石子游戏 题意/分析:k=2时,k倍动态减法游戏原型 例题 zoj2290 Game 题意/分析:FIB博弈,要求输出第一回合应取走的最小石头数。 例题 poj3922 A simple stonegame / hdu2486 A simple stone game / hdu2580 a simple stone game / zoj3599 Game 题意/分析:k倍动态减法游戏原型 (五)尼姆博弈的三种扩展形式 扩展形式1:限定每次取物上限 问题背景:有N堆物品,其中第i堆有pi个物品,每次去掉某一堆最多m个物品,两人轮流取物品,谁不能继续取谁就输了。 【结论1】令S为Pi对m+1取模后异或和的结果,若S=0则为P局面,否则为N局面。 证明:将pi分解为ri和ki,其中ki为(m+1)的倍数。如果对手在ri内取物,则按照Nim游戏的走法,若不然,假设A取x个,那么B就取(m+1-x)个,使得游戏保持原有必胜态或必败态。 例题 hdu1851 A Simple Game 题意/分析:Nim扩展形式1原型。 扩展形式2:每次允许从k堆中取物(Nimk问题) 问题背景:有N堆物品,其中第i堆有pi个物品,每次最多可以从k堆中选出若干物品去掉,两人轮流取物,谁不能继续取谁就输了。 【结论2】我们把pi这n个数转成二进制,然后每位分别相加,每位和%(k+1)即可。如果每一位结果都是0,则为P局面,否则为N局面。 证明:这里直接给出具体做法:设P1P2P3···Pn为n堆物品的数目。Pi为已标记的物品对,D0[i]和D1[i]分别表示所有已标记的物品堆中第i位为0和1的总数。 1)找出加法结果非0的最高位,设为W。 2)找出一个二进制第W位为1、而且未标记的物品堆Pi,将Pi标记,并把它的第W位由1改为0。对于Pi的第1到(W-1)位,逐个判断:第j位如果为0,则D0[j]++;否则D[1]++。 3)若更新后的S某一位非0,且S[i]+D0[i]>K,或S[i]-D1[i]<1,可以通过修改以前已标记的物品堆。 4)如果加法结果已经全部为0,则确认所有已经做得更改,并结束,否则转到1 。 扩展形式3:规定取物方向(阶梯博弈) 游戏情形:博弈在一列阶梯上进行,每个阶梯上放着若干个自然数,两个人进行阶梯博弈,每一步则是将一个阶梯上的若干个自然数移到前面去。以此类推,最后没有点可移动的人输。具有该问题背景的博弈称为阶梯博弈。 【结论3】把所有奇数阶梯看成N堆石子,把石子从奇数堆移动到偶数堆可以理解为拿走石子,即几个奇数堆的石子在做Nim游戏。 证明:假设我们是先手,所给的阶梯石子状态的奇数堆做Nim游戏,先手能必,按照能赢的步骤将奇数堆的石子移动到偶数堆。如果对手也是移动奇数堆,我们继续移动奇数堆。如果对手将偶数堆的石子移到奇数堆,那么我们将这些石子,再移到下一个偶数堆,这样就保持了奇数堆不变,保持了Nim游戏的性质。 例题 poj1704 Georgia and Bob/ hdu4315 Climbing the Hill 题意:从左到右n个格子,某些有石子,每格永远只能有一个石子,每次可以将某个石子向左移若干格,但不能跨越任何石子。两人轮流操作,谁无路可走谁输。 分析:奇异局势必定是两两棋子相邻为一组,前者移动左边的棋子,后者只需紧贴就可以了。所以无需考虑组与组之间的空隙,而组内棋子之间的距离相当于取石子。即阶梯博弈中,第i枚棋子与第i+1枚棋子的距离对应奇数堆的石子数,组和组之间的距离对应偶数堆的石子数。 例题 hdu3389 Game 题意:有n个编号为1到n的盒子,当两个盒子编号满足B 分析:我们将全部盒子分为两类,一类为编号%6余0,2,5的,一类为编号%6余1,3,4的,不难证明,所有操作都是在这两类之间进行,就化成了经典的阶梯博弈。 SG函数 (一)SG-组合游戏 应用SG函数解决问题时,组合游戏需要满足的条件: 1. 游戏有两个人参与,二者轮流做出决策。且这两个人的决策都对自己最有利。 2. 当有一人无法做出决策时游戏结束,无法做出决策的人输。无论二者如何做出决策,游戏可以在有限步内结束。 3. 游戏中的同一个状态不可能多次抵达。且游戏不会有平局出现。 4. 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关,而与游戏者无关。 我们使用SG函数评估游戏中的每一个子状态,其定义如下: 其中mex (minimal excludant)是定义在整数集合上的操作。它的自变量是任意整数集合,函数值是不属于该集合的最小自然数:。 事实上,在所有SG-组合游戏中,各状态之间都存在相应的联系,我们完全可以根据这种拓扑关系来逐一算出每个状态点的SG函数(事实上我们只要知道该状态点的SG函数值是否为0即可)。这样,我们就可以知道对于某一个状态,是先手必胜局还是先手必败局。上述方法的瓶颈在于没有充分利用SG-组合游戏问题的特殊性质。 (二)SG-组合游戏问题的特殊性质 【定义1】 考虑任意多个同时进行的SG-组合游戏,这些SG-组合游戏的和是这样一个游戏,在它进行的过程中,游戏者可以任意挑选其中的一个单一游戏进行决策,最终,没有办法进行决策的人输。 【性质1】 对于任意的局面,如果它的SG值为0,那么它的任何一个后继局面的SG值不为0 。 【性质2】 对于任意的局面,如果它的SG值不为0,那么它一定有一个后继局面的SG值为0 。 【定理1】 (SG定理)在我们每次只能进行一步操作的情况下,对于任何游戏的异或和,我们若将其中的任一单一SG-组合游戏换成数目为它的SG值的一堆物品,该单一SG-组合游戏的规则变成Nim游戏的规则,则游戏的异或和的胜负情况不变。 三类特殊的SG游戏: (1)、Anti-SG游戏 【定义2】Anti-SG游戏规定,决策集合为空的游戏者赢。其他规则与SG游戏相同。 【定理2】 (Anti-SG定理)对于任意一个Anti-SG游戏,如果我们规定当局面中所有的单一游戏的SG值为0时,游戏结束,则先手必胜当且仅当: 1)游戏的SG函数不为0时且游戏中某个单一游戏的SG函数大于1。 2)游戏的SG函数为0且游戏中没有单一游戏的SG函数大于1。 (2)、Multi-SG游戏 【定义3】Multi-SG游戏规定,在符合拓扑原则的前提下,一个单一游戏的后继可以为多个单一游戏,其他规则与SG游戏相同。 【定理3】Multi-SG游戏的仍然可以用SG函数来定义局面。 例题poj3537 Crosses and Crosses 题意:给定一个长度为n的棋盘,两人轮流下棋。并且每次下的棋不能与之前下的棋相邻。问是否先手必胜。 分析:简单的Multi-SG游戏,记忆化搜索求SG函数即可。 (3)、Every-SG游戏 【定义4】Every-SG游戏规定,对于还没有结束的单一游戏,游戏者必须对该游戏进行一步决策,其他规则与SG游戏相同。 【定义5】 在通过拓扑关系计算某一个状态点的SG函数时,对于SG值为0的点,我们需要知道最快几步能将游戏带入终止状态,对于SG值不为0的点,我们需要知道最慢几步游戏会被带入终止状态,我们用step函数表示这个值。 【定理4】 对于Every-SG游戏先手必胜当且仅大单一游戏中最大的step为奇数。 例题 hdu3595 GG and MM 题意:有N个游戏同时进行,每个游戏有两堆石子,每次从个数多的堆中取走数量少的数量的整数倍的石子。最后取完的胜利。问是否先手必胜。 分析:假设x>y,如果x/y=1,那么这一步是固定的,如果x/y>=2,那么谁拥有第一对这样的xy,就可以将所有的x/y>=2控制在自己手中,到了最后一个,便可以控制奇偶,让自己获胜,以此得到最大的步数,判断奇偶。 (三)经典的SG组合游戏 (1)“翻硬币”游戏 游戏情形:N枚硬币排一排,有的正面朝上(H),有的反面朝上(T),我们从左开始对硬币按1到N编号。游戏者根据某些约束翻硬币,但他所翻动的硬币中,最右边的必须是从正面翻到反面。谁不能翻谁输。 【结论】局面的SG值为局面中每个正面朝上的棋子单一存在时的SG值的异或和。 证明:我们先确定数学归纳法的顺序。对于任何一个正面朝上的硬币,我们设它的分值为2的k次方(它为从左数第k枚硬币),一个局面的分值为所有正面朝上的硬币的分值和。显然,对于任意一个局面,它的所有后继局面的分值小于它。我们以局面的分值作为归纳顺序。 1)分值为0和1的局面符合要求(对应只有一枚硬币的情况) 2)假设分值小于等于k的局面符合要求。我们证明分值为(k+1)的局面符合要求。 对于分值为(k+1)的局面,我们考虑它的某一次决策,可以认为最右边的改动位是去掉一个正面朝上的硬币,其他改动是添加了一个正面朝上的硬币。这样,可以将决策看成去掉了某一堆石子(最右边的改动位),添加了一个它的后继石子堆(其他改动位),使得这个决策与Nim游戏完全等价。 由该结论得到,我们只需要计算每个类似于SG(TH)、SG(TTH)···SG(TT···TH)这样的值,异或起来即可。下面转自欢娘的博客。 约束条件1:每次只能翻一个硬币。 很容易得到结论,当正面朝上的硬币为奇数个时,SG值为1,先手必胜;否则SG值为0,先手必败。 约束条件2:每次能翻转一个或两个硬币(不用连续)。 每个硬币的SG值为它的编号,初始编号为0,与NIM游戏是一样的。 如果对于一个局面,把正面硬币的SG值异或起来不等于0,既a1^a2^a3^…^an==x,对于an来说一定有an'=an^x 如果an'==0,意思就是说,把an这个值从式子中去掉就可以了。对应游戏,就是把编号为an的正面硬币翻成背面就可以了。因为an^x==0,而a1^a2^a3^…^an==x,即an^a1^a2^a3^…^an==0,即a1^a2^a3^…^an-1==0,只要在原来的x里面去掉an就可以了。 如果an'!=0,意思就是说,把an这个值从式子中去掉后再在式子中加上an',an' an'=a1^a2^a3^…^an-1,所以在x中去掉an后,要对an'进行异或,也就是翻转,正转反,反转正。 约束条件3:每次必须连续翻转k个硬币。 我们以k==3为例。 我们计算的是个数为N的硬币中,其中最后一个硬币为正面朝上,的sg值。 当N==1时,硬币为:正,先手必输,所以sg[1]=0。 当N==2时,硬币为:反正,先手必输,所以sg[2]=0。 当N==3时,硬币为:反反正,先手必胜,所以sg[3]=1。 当N==4时,硬币为:反反反正,先手操作后为:反正正反,子状态局面的SG=0^1=1,那么sg[4]=0。 当N==5时,硬币为:反反反反正,先手操作后为:反反正正反,子状态局面的SG=1^0=1,那么sg[5]=0。 当N==6时,硬币为:反反反反反正,先手操作后为:反反反正正反,子状态局面的SG=0^0=0,那么sg[6]=1。 根据观察,可以知道,从编号为1开始,sg值为:001001 001 001…… 根据观察,可以知道,sg的形式为000…010…01,其中一小段0的个数为k-1。 约束条件4:每次翻动一个硬币后,必须翻动其左侧最近三个硬币中的一个,即翻动第x个硬币后,必须选择x-1,x-2,x-3中的其中一个硬币进行翻动,除非x是小于等于3的。(SubtractionGames) 当N==1时,硬币为:正,先手必赢,所以sg[1]=1。 当N==2时,硬币为:反正,先手必赢,因为先手可以翻成反反或正反,可能性为2,所以sg[2]==2。 当N==3时,硬币为:反反正,先手操作后可以为:反正 位置x:1 2 3 4 5 6 7 8 9 10 11 12 13 14... sg[x]: 1 2 3 0 1 2 3 0 1 2 3 0 1 2… 这个与每次最多只能取3个石子的取石子游戏的SG分布一样,同样还有相似的这类游戏,约束条件5也是一样。 约束条件5:每次必须翻动两个硬币,而且这两个硬币的距离要在可行集S={1,2,3}中,硬币序号从0开始。(Twins 游戏) 当N==1时,硬币为:正,先手必输,所以sg[0]=0。 当N==2时,硬币为:反正,先手必赢,所以sg[1]=1。 当N==3时,硬币为:反反正,先手必赢,所以sg[2]=2。 当N==4时,硬币为:反反反正,先手必赢,所以sg[3]=3。 当N==5时,硬币为:反反反反正,先手必输,所以sg[4]=0。 位置x:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14... sg[x]: 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2… 约束条件6:每次可以翻动一个、两个或三个硬币。(Mock Turtles游戏) 初始编号从0开始。 当N==1时,硬币为:正,先手必胜,所以sg[0]=1. 当N==2时,硬币为:反正,先手必赢,先手操作后可能为:反反或正反,方案数为2,所以sg[1]=2。 当N==3时,硬币为:反反正,先手必赢,先手操作后可能为:反反反、反正反、正反正、正正反,方案数为4,所以sg[2]=4。 位置x:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14... sg[x]: 1 2 4 7 8 111314 16 19 21 22 25 26 28… 看上去sg值为2x或者2x+1。我们称一个非负整数为odious,当且仅当该数的二进制形式的1出现的次数是奇数,否则称作evil。所以1,2,4,7是odious因为它们的二进制形式是1,10,100,111.而0,3,5,6是evil,因为它们的二进制形式是0,11,101,110。而上面那个表中,貌似sg值都是odious数。所以当2x为odious时,sg值是2x,当2x是evil时,sg值是2x+1. 这样怎么证明呢?我们会发现发现, evil^evil=odious^odious=evil evil^odious=odious^evil=odious 假设刚才的假说是成立的,我们想证明下一个sg值为下一个odious数。注意到我们总能够在第x位置翻转硬币到达sg为0的情况;通过翻转第x位置的硬币和两个其它硬币,我们可以移动到所有较小的evil数,因为每个非零的evil数都可以由两个odious数异或得到;但是我们不能移动到下一个odious数,因为任何两个odious数的异或都是evil数。 假设在一个Mock Turtles游戏中的首正硬币位置x1,x2,…,xn是个P局面,即sg[x1]^…^sg[xn]=0.那么无可置疑的是n必定是偶数,因为奇数个odious数的异或是odious数,不可能等于0。而由上面可知sg[x]是2x或者2x+1,sg[x]又是偶数个,那么x1^x2^…^xn=0。相反,如果x1^x2^…^xn=0且n是偶数,那么sg[x1]^…^sg[xn]=0。这个如果不太理解的话,我们可以先这么看下。2x在二进制当中相当于把x全部左移一位,然后补零,比如说2的二进制是10,那么4的二进制就是100。而2x+1在二进制当中相当于把x全部左移一位,然后补1,比如说2的二进制是10,5的二进制是101。现在看下sg[x1]^…^sg[xn]=0,因为sg[x]是2x或者2x+1,所以式子中的2x+1必须是偶数个(因为2x的最后一位都是0,2x+1的最后一位都是1,要最后异或为0,2x+1必须出现偶数次)。实际上的情况可能是这样的: MT游戏当中的P局面是拥有偶数堆石子的Nim游戏的P局面。 约束条件7:每次可以连续翻动任意个硬币,至少翻一个。(Ruler游戏) 初始编号从1开始。 那么这个游戏的SG函数是g(n)=mex{0,g(n-1),g(n-1)^g(n-2),…,g(n-1)^…^g(1)} 根据SG函数可以得到SG值表如下。 位置x:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16... g(x): 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16… 所以sg值为x的因数当中2的能达到的最大次幂。比如14=2*7,最大1次幂,即2;16=2*2*2*2,最大4次幂,即16。 这个游戏成为尺子游戏是因为SG函数很像尺子上的刻度。 约束条件8:每次必须翻转4个对称的硬币,最左与最右的硬币都必须是从正翻到反。(开始的时候两端都是正面)(Grunt游戏) 这是Grundy游戏的变种,初始编号从0开始。 当首正硬币位置为0,1,2时是terminal局面,即 终结局面,sg值都是0。当首正硬币位置n大于等于3的时候的局面可以通过翻0,x,n-x,n四个位置得到(其中x 这就像是把一堆石子分成两堆不同大小石子的游戏,也就是Grundy游戏。 例题hdu3537 Daizhenyang’s Coin 题意/分析:约束条件6原型。 二维 游戏情形:在一个n*n的方格阵中,每个格子里放一枚硬币,有的正面朝上(H),有的反面朝上(T)。两个人做游戏,轮流翻硬币。规则是这样的:选一个跟方格阵平行的矩形,将它四个角上的硬币翻转,并且要求矩形的右下角必须从正面翻到反面。不能操作的人就输了。判断某一种状态是先手必胜还是后手必胜。 基本理论: 1)Nim和⊕ 若x可以分解为独立的若干状态x1,x2,···,xk,则 2)Nim积 定义: 它是一种二元运算,运算法则如下: 【Tartan定理】如果的游戏,其中是第i个游戏为xi时的SG函数值(1<=i<=n),那么这个游戏的SG函数值就是各个子游戏SG函数值的Nim积。 计算Nim积的方法:利用对于的运算性质,递归处理,将其转化为小的数,再用定义去计算。 考虑原来一维的情况。n个硬币排成一行,每次可以去一个正面朝上的硬币,和它左边的任一枚硬币,将它们翻转。两人轮流操作,不能操作者输。由于每个状态可以分解成只有一个反面朝上的子状态,我们只要考虑这种情况的SG()函数即可。设H坐标有n个T的状态:,根据SG(x)的定义,我们可以得出:。 回到二维情况:根据游戏论理论,对于表示在(x,y)格中有唯一H状态的SG函数值,则 。这样我们只需要计算每一个二维状态正面朝上的所有位置的的值,求它们的Nim和。 例题 hdu3404 Switch lights 题意/分析:二维的翻硬币游戏。 例题 poj3533 Light SwitchingGame 题意:给定一个边长为1000的立方体最初的灯状态,每次可以翻动一个立方体内的灯,要求(x2,y2,z2)灯必须亮着。不能走的人输。给你n个亮灯的坐标,问后手是否能赢。 分析: (2)图游戏模型 如果我们把游戏中的某一个局面看作一个顶点,把局面之间的转换用边来表示,那么很多游戏都可以转化为图游戏模型。 一些图游戏可以通过SG函数来判定先手的胜负情况。一个图G=(V,E)的SG函数定义在v上的一个非负整数函数: 【性质】对于一个图游戏,如果图的当前状态等于0,那么先手必败,否则必胜。 例题poj2599 A funny game 题意:机场作为节点,航线作为边,组成一棵含n-1条边的无向树,两个人从某节点出发,轮流顺边移动,做过的节点不能再走,直至有一个人不能走了,该人算输。计算先手的输赢。 分析:利用dfs计算SG函数即可。 例题hdu1524 / poj2425 A Chess Game 题意:在一个有向无环图上,分布着一些棋子,两个玩家轮流操作,每次可以将一个棋子沿边移动一步,问是否先手必胜。 分析:利用dfs计算每个棋子对应的SG函数,异或起来即可。 (3)无向图的删边游戏 <1> 树的删边游戏 规则:给出一个有N个点的树,有一个点作为树的根节点。游戏者轮流从树中删去边,删去一条边后,不与根节点相连的部分将被移走。谁无路可走谁输。 【定理】 叶子节点的SG值为0;中间节点的SG值为它的所有子节点的SG值加1后的异或和。 证明:1.一个节点和两个节点的情况显然成立。 2.我们假设小于K个节点的任意情况都成立,下面证明(K+1) 个节点的情况也成立。下分两部分证明:证明根节点只有一个孩子的情况符合要求;‚证明根节点有多个孩子的情况符合要求。 先证第一部分:我们假设树G的根为A,A只与B相连,图中共有N+1个节点,去掉A后以B为根节点的图为G’ 再证明第二部分: 第二部分的证法类似于NIM和,不再累述。 例题 hdu3094 A tree game 题意/分析:树删边游戏原型。 例题 hdu3197 Game 题意/分析:多个树的树删边游戏。 例题 hdu3590 PP and QQ 题意/分析:多个树删边,Anti-SG游戏。 例题 poj3710 Christmas Game 题意:有N个局部连通的图,Harry和Sally轮流从图中删边,删去一条边后,不与根节点相连的部分将被移走。Sally为先手。图是通过从基础树中加一些边得到的。所有行程环保证不共用边,且只与基础树有一个公共点。谁无路可走谁输。 分析:我们分析其中的一个性质:环不共用边且与基础树只有一个公共点。所以体题中所有的环都是从树中某一个点连出又连回同一个点的简单环。我们得到如下性质:1、对于长度为奇数的环,去掉其中任意一个边之后,剩下的两个链长度同奇偶,异或之后的SG值不可能为奇数,所以它的SG值为1;2、对于长度为偶数的环,去掉其中任意一个边之后,剩下的两个链长度奇偶性不同,异或之后的SG值不能为0,所以它的SG值为0。通过这两条性质,我们可以去掉所有偶环,将所有奇环变为长度为1的链。然后利用树删边游戏的结论计算即可。 <2>无向图的删边游戏 无向图的删边游戏:一个无向联通图,有一个点作为图的根。游戏者轮流从图中删去边,删去一条边后,不与根节点相连的部分将被移走。谁无路可走谁输。 【FusionPrinciple定理】 我们可以对无向图做如下改动:将图中的任意一个偶环缩成一个新点,任意一个奇环缩成一个新点加一个新边;所有连到原先环上的边全部改为与新点相连。这样的改动不会影响图的SG值。 通过这个定理,我们可以将任意一个无向图转化为树结构,将问题转化为了树删边游戏。 (四)其他题目 例题 hdu3032 Nim or not Nim? 题意: 有n堆石子,两人轮流从任一堆中取任意个石子(至少一个),或者将一堆分成两个小的堆。取走最后一个石子的人为赢家。问先手是否有必胜策略。 分析:由SG的性质可知,我们只要求出每一堆的SG的值异或起来就可以得到答案。考虑每一堆的情况。当n=0时,SG(0)=0;当n=1时,SG(1)=1;当n=2时,后继状态有0,1,(1,1),SG值分别为0,1,0,我们可以得到SG(2)=2;当n=3时,后继状态有0,1,2,(1,2),SG值分别为0,1,2,3,我们得到SG(3)=4;当n=4时,后继状态有0,1,2,3,(1,3),(2,2),SG值分别为0,1,2,4,2,0,我们得到SG(4)=3。接下来用数学归纳法可得到SG(4*k)=4*k-1,SG(4*k+1)=4*k+1,SG(4*k+2)=4*k+2,SG(4*k+3)=4*k+4。 例题 hdu1404 / zoj2725Digital Deletions 题意:一串由0~9组成的数字,可以进行两个操作:1、把其中一个数变为比它小的数;2、把其中一个数字及其右边的所以数字删除。两人轮流进行操作,最后把所以数字删除的人获胜,问前者胜还是后者胜。 分析:用记忆化搜索暴力求SG即可。 例题 hdu1536/hdu1944/poj2960S-Nim 题意:Nim游戏,不过每次取走的石子数必须是集合S中的元素。 分析:用记忆化搜索暴力求SG即可。 例题 zoj2083 Win the Game 题意:给定一个长度为n的线段,两个玩家轮流截出一段长度为2的线段,不能操作者输。问是否先手必胜。 分析:用记忆化搜索暴力求SG即可。 例题 hdu1848 Fibonacci againand again 题意:Nim游戏,不过每次取走的石子数必须是Fibonacci数。 分析:用记忆化搜索暴力求SG即可。 例题 poj2311 Cutting Game 题意:给定一个n*m的纸片,每一次可以把一部分剪成两部分,谁剪出1*1就赢了,问是否先手必胜。 分析:暴力求SG函数即可。 例题 hdu2873 Bomb Game 题意:给你一个n*m的地图,地图上有一些炸弹。两个玩家轮流操作,选择一个炸弹,将其分裂成两个分别拥有相同行数和相同列数,且对应行数、列数小于被选的那个的炸弹的值。如果该炸弹处在边界上,则只分裂为1个。分裂后的炸弹的位置由当前玩家选择。如果两个炸弹遇到了一起,或者炸弹被放置在(1,1)点,则该点所有炸弹都将消失。问是否先手必胜。 分析:利用SG定理,并求出每个炸弹对应的SG值异或起来即可。 例题 hdu2999 Stone Game, Whyare you always there? 题意:给出一串石头,和一个集合,每次取出若干连续的石头(数量必须为集合中的),最后取完的获胜,问是否先手必胜。 分析:对于每一次决策,都将一串连续的石头分割成两部分(每一部分都可以为0),递归求解SG函数,不过要注意优化常数。 例题 hdu3980 Paint Chain 题意:两个人在一个由n个玻璃球组成的一个圆环上玩涂色游戏,游戏的规则是:1、每一轮,每轮选择一个长度为m的连续的、没有涂过色的玻璃球串涂色。2、不能涂色的那个人输掉游戏。 分析:和hdu2999题目基本一样,固定每次只能取m个,第一次破链为环,之后就跟hdu2999完全一样了,用记忆化搜索暴力求SG函数。 例题 hdu4111 Alice and Bob 题意:有n堆石子,每堆石子有一个数目,现有两个人博弈,一共两种操作:1、从某非空堆拿掉一个石子。2、合并两个非空堆的石子。先取完着胜利。问是否先手必胜。 分析:如果每堆石子数都大于1,那么最后结果肯定相当于所有的堆合并为一堆后,然后再一个一个拿掉的结果,且对手无法阻止。如果有一些堆石子数量为1的话,则不满足之前的性质,但是我们可以单独考虑这些,即我们用(x,y)来表示当前状态,其中x表示石子数为1的堆数,y表示其它堆合并并取完的步数。 例题 hdu1729 Stone Game 题意:给出一些盒子,盒子有容量限制,给出初始石子数,每次给某一个盒子中添加石头。添加的数量小于等于盒子中已有的石子数的平方。 分析:我们知道对于容量S,当然石子数C,如果C+C*C 使用数学工具surreal number应对不平等的组合游戏 (一)surreal number的构造 【定义1】一个surrealnumber由两个集合组成。我们称这两个集合“左集合”与“右集合”。通常情况下,我们会将surreal number写作{L|R},其中L表示左集合,R表示右集合。这两个集合中的元素也为surreal number,且右集合中不存在一个元素x,使得左集合中存在一个元素y满足x<=y。 【定义2】对于surrealnumber 和 ,我们称x<=y当且仅当不存在使得以及不存在使得。 不难看出上面的两个定义都是基于递归的形式给出的,通过上面的两个定义,我们可以尝试构造surreal number。 由定义1可知,一个surrealnumber 由左集合与右集合组成,且这两个集合的元素也必须为surreal number。但是我们目前连一个surrealnumber 也不知道, 因此只能令 L为空集,R为空集,得出。我们令其为0 ,并称其为在0天出生的。我们下来可以构造出两个新的集合{|0}=-1,{0|}=1,我们称其是在第一天出生的。利用0,1,-1作为左集合,右集合的元素,我们可以构造出17个合法的surrealnumber,我们称这17个surreal number是在第2天出生的。利用定义2,我们可以证明1<{1|}和-1>{|-1},因此我们令{1|}=2,{|-1}=-2。另外我们发现0<{0|1}<1,由于在稍后的加法运算中会有{0|1}+{0|1}=1,因此我们令{0|1}=1/2。同理{-1|0}=-1/2。 因此我们现在有7个surrealnumber:-2,-1,-1/2,0,1/2,1,2,虽然在第2天出生的合法的surrealnumber还有13个,但是它们值等价于这7个中的一个。例如{-1|1}=0。以此类推,我们可以构造出所有形如j/2^k的有理数。我们可以定义如下函数来建立部分有理数与surreal number的对应关系,我们称这个函数为达利函数: (二)surreal number 的一些基本定理 【定理1】 对于一个surrealnumber x={L|R},x大于L中的任意一个元素且小于R中的任意一个元素。 【定理2】 对于一个surrealnumber x={L|R},若集合L中有最大元素lmax,那么{lmax|R}=x;类似地,若集合R中有最小元素rmax,那么{L|rmax}=x。 【定理3】 设a到b之间最早出生的surrealnumber是在第i天出生,那么在a到b之间且在第i天出省的surrealnumber 只有一个。 【定理4】 如果a (三)surreal number的运算法则 【定义3】 对于surrealnumber 和,它们的加法运算被定义为: 其中对于集合X与surrealnumber y,。其结束条件为。 【定义4】 对于surrealnumber ,x的相反数为: ,其中对于集合X,。其结束条件为:-0=-{|}={|}=0。 【定义5】 对于surrealnumber x和y,x-y=x+(-y) 【定理5】 对于surrealnumber 和, 也是一个合法的surreal number。 【定理6】surreal number 的加法满足交换律,即x+y=y+x. 【定理7】surreal number 的加法满足结合律,即(x+y)+z=x+(y+z)。 (三)组合游戏的定义与表示 在介绍surreal number 在组合游戏中的应用之前,我们先来看看这里所讲的组合游戏的定义: 1、游戏有2 名参与者,通常称为玩家L和玩家R。 2、游戏过程中的任意时刻有确定的状态。 3、参与者操作时将游戏从当前状态转移到另一状态,规则规定了在任意一个状态时,参与者可以到达的状态集合。 4、参与者轮流进行操作。 5、在游戏处于某状态,当前参与者不能进行操作时,游戏结束。本节只讨论最先不能进行操作者输的情况。 6、无论参与者做出怎样的操作,游戏总会在有限步数之内结束(没有平局)。 7、参与者拥有游戏本身,和游戏过程的所有信息,比如规则、自己和对手之前的操作。 由上面的定义可以看出,我们这里所讲的游戏是由状态组成的。对于一个游戏,如果它当前处于状态P,玩家L可以转移到的状态的集合为PL,玩家R可以转移到的状态的集合为PR,那么我们把这个游戏写作P={PL|PR}。所有的surrealnumber 都是游戏,但是并非所有的游戏都是surreal number,因为对于游戏P={PL|PR},并没有要求集合PL中的任意元素都要小于集合PR中的任意元素。因此我们下面讨论的游戏,都是可以表示为surreal number的游戏。 (四)surreal number 在组合游戏中的应用 对于一个游戏G,如果玩家L和玩家R都采用最优策略进行游戏,且游戏G等价于surreal number x,那么有如下结论: 1、如果x > 0,那么无论先手还是后手,玩家L都会获胜。 2、如果x < 0,那么无论先手还是后手,玩家R都会获胜。 3、如果x = 0,那么谁后手谁获胜。 上面的结论可以用类似于数学归纳法的思想来证明: 当x > 0时,如果是玩家L先手,从x是surrealnumber可知,玩家L总可以将x转移到一个大于等于0的状态;如果是玩家R先手,那么玩家R只能将x转移到一个大于0的状态,因此任意时刻玩家L的可选决策集合都不为空集,所以这种情况无论先手还是后手,玩家L都会获胜。 当x < 0时,玩家L只能将x转移到一个小于0的状态,而玩家R总可以将x转移到一个小于等于0的状态,因此任意时刻玩家R的可选决策集合都不为空集,所以无论先手还是后手,玩家R都会获胜。 当x = 0时,如果是玩家L先手,那么他只能将x转移到一个小于0的状态,这样玩家R会获胜;如果是玩家R先手,那么他只能将x转移到一个大于0的状态,这样玩家L会获胜。所以,对于x= 0的情况,谁后手谁获胜。 很多时候,一个游戏G会被分解成n个不相交的子游戏G1,G2, … Gn,对G的每次操作等价于从n个子游戏中选取一个来进行操作。这种情况,我们称游戏G是游戏G1, G2, …Gn的和,写作G = G1 + G2 +…+Gn。有n堆石子的Nim游戏就是一个经典的例子。 对于这类可分解的游戏,surreal number能够对其较好地进行分析,因为有如下定理: 【定理8】 如果游戏G等价于surreal number x,游戏H等价于surreal number y,那么游戏G+H等价于surrealnumber x+y。 (五)例题poj2931 Procrastination 题意: 有一个叫Procrastination的游戏,规则如下: 游戏一开始有四座由正方体叠成的塔,且所有的正方体要么是黑色,要么白色。 有两个玩家L和R,游戏开始后,两个玩家轮流进行操作。 每次操作,玩家要选定一个正方体,然后拿走该正方体以及位于该正方体上面的所有正方体,并且规定玩家L只能选定白色的正方体,玩家R只能选定黑色的正方体。 最先不能进行操作的人输。 对于一个初始局面,如果玩家L无论先手还是后手都能获胜,那么我们称这是一个W-configuration。另外我们定义子局面C表示一个由三座塔组成的局面。一个完整的游戏局面可以由一个子局面C以及一座塔T构成,写作(C, T)。对于两个子局面C1和C2,我们称C1不差于C2当且仅当对于任意的一座塔T,在(C2, T)为W-configuration时(C1, T)也为W-configuration。 给出两个子局面C1和C2,问是否C1不差于C2。数据规模:对于每座给出的塔,它的高度n满足0<=n<=50。 分析: 我们对每个柱子进行估价: 1)柱子最下面所有的正方体分值的绝对值都是1,上面的正方体分值的绝对值依次为它下面的正方体分值的绝对值的一半。 2)黑色正方体的分值为负数,白色正方体的分值为正数。 3)柱子的得分为它上面所有正方体的分数和。 局面的分值为所有柱子的分值和。 我们先证明三个结论: 【结论1】 白手作出的决策只会使局面的分值变小,黑手作出决策只会使局面的分值变大。 证明:白手拿走的正方体的分数一定大于它上面的所有正方体的分数和,所以局面的分值一定变小,黑手同理。 【结论2】 如果当前分值大于0,白手可以保证他做出决策之后,局面的分值大于等于0。 证明:如果所有的柱子都为同色柱子,则当前的分值至少为1,显然,白手拿走最上面的一个白子能使得最后的分值大于等于0,符合要求;否则,至少有一堆为异色柱子。我们找最上面的正方体分值最小的柱子,设分值为K,显然当前的分值大于等于K;我们拿走最上面的白色正方体,则局面的分值减小K,由“当前的分值大于等于K”可知,取完后,局面的分值大于等于0。 【结论3】 一个局面的分值大于0时,白手必胜(不论先后手);一个局面的分值小于0时,黑手必胜(不论先后手);一个局面的分值等于0时,先手必败。 证明:当局面的分值大于0时,如果白手先手,他可以使得他操作完之后,局面的分值大于等于0,之后黑手操作,局面的分值一定变为大于0,那么最后一定是黑手先五路可走;如果白手后手,黑手操作完之后,局面的分值一定大于0,与上种情况相同,最后一定还是黑手先无路可走。当局面的分值等于或小于0时,类比上面的证明,不难得出本结论。 【定理】 “对于任意的柱子CC,若AC为白手先手必胜局,则BC一定为白手先手必胜局”当且仅当BB的分值大于等于AA的分值。 有了这个定理,我们就可以通过估值来解题了。 参考资料: 1. 《程序设计解题策略》 吴永辉 王建德 2. 《博弈类题目》 cxlove 3. 《组合游戏略述——浅谈SG游戏的若干拓展及变形》贾志豪 4. 《从“k倍动态减法游戏”出发探究一类组合游戏问题》曹钦翔 5. 《翻硬币游戏》 欢娘 6. 《浅谈如何解决不平等博弈问题》 方展鹏 7. cxlove的部分题解 8. PoPoQQQ的部分题解