C#数据结构-八大排序算法
阅读目录
1. 冒泡排序
2. 选择排序
3. 插入排序
4. 希尔排序
5. 快速排序:初始快速排序、三向切分的快速排序(快速排序的优化版)
6. 堆排序
7. 归并排序:数组版本、List版本
8. 桶排序
下面所有的代码,都已经经过vs测试。
首先,通用的交换函数Swap:
private static void Swap(ref int a, ref int b)
{
int temp = a;
a = b;
b = temp;
}1. 冒泡排序
基本思想:依次比较相邻的两个元素,如果前面的数据大于后面的数据,就将两个数据进行交换
C#算法实现:
///
/// 冒泡排序
/// 依次比较相邻的两个元素,如果前面的数据大于后面的数据,就将两个数据进行交换
/// 测试用例:4 3 2 1
/// i = 0;
/// j = 1; 3 4 2 1
/// j = 2; 3 2 4 1
/// j = 3; 3 2 1 4
///
/// i = 1;
/// j = 1; 2 3 1 4
/// j = 2; 2 1 3 4
///
/// i = 2;
/// j = 1; 1 2 3 4
///
private static void BubbleSort(int[] arr, int length)
{
for (int i = 0; i < length - 1; i++)
{
for (int j = 1; j < length - i; j++)
{
if (arr[j] < arr[j - 1])
{
Swap(ref arr[j - 1], ref arr[j]);
}
}
}
}2. 选择排序
基本思想:在要排序的一组数中,假设第一个元素时最小值,依次与后面的元素比较,如果有更小的值,交换。继续遍历元素,依次找到最小的值,进行交换,最后完成排序。
C#算法实现:
///
/// 选择排序
/// 在要排序的一组数中,选出最小的一个数与第i个位置的数交换,之后依次类推(i=0,1,2,3...)
/// 测试用例:49 38 65 32
/// i = 0,min = 3, 32 38 65 49
/// i = 1, min = 1, 32 38 65 49
/// i = 2, min = 3, 32 38 49 65
///
private static void SelectSort(int[] arr, int length)
{
for (int i = 0; i < length - 1; i++)
{
int min = i;
for (int j = i + 1; j < length; j++)
{
if (arr[j] < arr[min])
{
min = j;
}
}
//当在此次遍历中,如果没有比arr[i]更小的值,则不用交换
if (min != i)
{
Swap(ref arr[i], ref arr[min]);
}
}
}3. 插入排序
基本思想:将原来的无序数列看成含有一个元素的有序序列和一个无序序列,将无序序列中的值依次插入到有序序列中,完成排序。
C#算法实现:
///
/// 插入排序
/// 将原来的无序数列看成含有一个元素的有序序列和一个无序序列,将无序序列中的值依次插入到有序序列中,完成排序
/// 测试用例: 49 38 65 32
/// i = 1, j = 0; a[0] > a[1] YES 交换 38 49 65 32
/// i = 2, j = 1; a[1] > a[2] NO 不交换
/// i = 2, j = 0; a[0] > a[1] NO 不交换
/// i = 3, j = 2; a[2] > a[3] YES 交换 38 49 32 65
/// i = 3, j = 1; a[1] > a[2] YES 交换 38 32 49 65
/// i = 3, j = 0; a[0] > a[1] YES 交换 32 38 49 65
///
private static void InsertionSort(int[] arr, int length)
{
//将a[0]作为有序序列,从索引1开始遍历无序序列
for (int i = 1; i < length; i++)
{
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--)
{
Swap(ref arr[j], ref arr[j + 1]);
}
}
}4. 希尔排序
基本思想:在插入排序的基础上加入了分组策略,将数组序列分成若干子序列分别进行插入排序。
C#算法实现:
///
/// 希尔排序
/// 在插入排序的基础上加入了分组策略
/// 将数组序列分成若干子序列分别进行插入排序
/// 测试用例: 49 38 65 32
/// gap = 2;
/// i = 2, j = 0; a[0] > a[2] NO
/// i = 3, j = 1; a[1] > a[3] YES 交换 49 32 65 38
///
/// gap = 1;
/// i = 1, j = 0; a[0] > a[1] YES 交换 32 49 65 38
/// i = 2, j = 1; a[1] > a[2] NO
/// i = 3, j = 2; a[2] > a[3] YES 交换 32 49 38 65
/// i = 3, j = 1; a[1] > a[2] YES 交换 32 38 49 65
/// i = 3, j = 0; a[0] > a[1] NO
///
///
///
private static void ShellSort(int[] arr, int length)
{
for (int gap = length / 2; gap > 0; gap = gap / 2)
{
//插入排序
for (int i = gap; i < length; i++)
{
for (int j = i - gap; j >= 0 && arr[j] > arr[j + gap]; j -= gap)
{
Swap(ref arr[j], ref arr[j + gap]);
}
}
}
}5. 快速排序
基本思想:采用分治的思想,对数组进行排序,每次排序都使得操作的数组部分分成以某个元素为分界值的两部分,一部分小于分界值,另一部分大于分界值。分界值一般称为“轴”。一般是以第一个元素为轴,将数组分成左右两部分,然后对左右两部分递归操作,直至完成排序。
C#算法实现:
///
/// 快速排序
/// 采用分治的思想,对数组进行排序,每次排序都使得操作的数组部分
/// 分成以某个元素为分界值的两部分,一部分小于分界值,另一部分大于分界值。分界值一般称为“轴”
/// 一般是以第一个元素为轴,将数组分成左右两部分,然后对左右两部分递归操作,直至完成排序。
/// 测试用例: 14 11 25 37 9 28
/// 1.以第一个元素L = 0为最初的轴,pivot = 14
/// 2.从下标R = 5开始,从后向前找到比pivot 14小的数9,此时L = 0,R = 4,赋值给arr[L] = arr[R], L++
/// 9 11 25 37 9 28
/// 3.从下标L = 1开始,从前向后找到比pivot 14大的数25,此时L = 2,R = 4,赋值给arr[R] = arr[L],R--
/// 9 11 25 37 25 28
/// 4.在新的L = 2位置上设置新的轴, pivot = 14, arr[L] = pivot
/// 9 11 14 37 25 28
/// 5.然后,对比新的轴小的部分和比新的轴大的部分分别递归排序,直至完成排序
///
///
/// 数组的0下标
/// 数组的Length - 1下标
private static void QuickSort(int[] arr, int left, int right)
{
if (left < right)
{
int L = left;
int R = right;
int pivot = arr[L];
while (L < R)
{
//从后向前找出比pivot小的数
while (L < R && arr[R] > pivot)
{
R--;
}
//找到比pivot小的数,赋值给arr[L]
if (L < R)
{
arr[L] = arr[R];
L++;
}
//从前向后找出比pivot大的数
while (L < R && arr[L] < pivot)
{
L++;
}
//找到比pivot大的数,赋值给arr[R], 也就是之前比pivot小的数的位置
if (L < R)
{
arr[R] = arr[L];
R--;
}
}
//在新的L位置设置新的轴
arr[L] = pivot;
//对比新的轴小的部分递归排序
QuickSort(arr, left, L - 1);
//对比新的轴大的部分递归排序
QuickSort(arr, L + 1, right);
}
}三向切分的快速排序
快速排序在实际应用中会面对大量具有重复元素的数组。相比原生的快排,有巨大的改进潜力。(从O(nlgn)提升到O(n))
E.W.Dijlstra(对,就是Dijkstra最短路径算法的发明者)提出的算法是:
对于每次切分:从数组的左边到右边遍历一次,维护三个指针,其中lt指针使得元素(arr[0]-arr[lt-1])的值均小于切分元素;gt指针使得元素(arr[gt+1]-arr[N-1])的值均大于切分元素;i指针使得元素(arr[lt]-arr[i-1])的值均等于切分元素,(arr[i]-arr[gt])的元素还没被扫描,切分算法执行到i>gt为止。每次切分之后,位于gt指针和lt指针之间的元素的位置都已经被排定,不需要再去处理了。之后将(lo,lt-1),(gt+1,hi)分别作为处理左子数组和右子数组的递归函数的参数传入,递归结束,整个算法也就结束。
三向切分的示意图:
///
/// 快速排序在实际应用中会面对大量具有重复元素的数组。相比原生的快排,有巨大的改进潜力。(从O(nlgn)提升到O(n))
/// E.W.Dijlstra(对,就是Dijkstra最短路径算法的发明者)提出的算法是: 对于每次切分:从数组的左边到右边遍历一次,维护三个指针,
/// 其中lt指针使得元素(arr[0]-arr[lt-1])的值均小于切分元素;gt指针使得元素(arr[gt+1]-arr[N-1])的值均大于切分元素;
/// i指针使得元素(arr[lt]-arr[i-1])的值均等于切分元素,(arr[i]-arr[gt])的元素还没被扫描,切分算法执行到i>gt为止。
/// 每次切分之后,位于gt指针和lt指针之间的元素的位置都已经被排定,不需要再去处理了。
/// 之后将(lo,lt-1),(gt+1,hi)分别作为处理左子数组和右子数组的递归函数的参数传入,递归结束,整个算法也就结束。
///
///
///
/// arr.Length - 1
private static void QuickSort_Optimization(int[] arr, int low, int hi)
{
//去除单个元素或者没有元素的情况
if (low < hi)
{
int lt = low;
int i = low + 1;//第一个元素是切分元素,所以i从low+1开始
int gt = hi;
int pivot = arr[lt];
while (i <= gt)
{
//小于切分元素放在lt左边,指针lt和i整体右移
if (arr[i] < pivot)
{
Swap(ref arr[i], ref arr[lt]);
i++;
lt++;
}
//大于切分元素放在gt右边,指针gt左移
else if (arr[i] > pivot)
{
Swap(ref arr[i], ref arr[gt]);
gt--;
}
//等于切分元素,指针i++
else
{
i++;
}
}
//lt-gt之间的元素已经排定,只需对lt左边和gt右边的元素进行递归排序
//对比新的轴小的部分递归排序
QuickSort_Optimization(arr, low, lt - 1);
//对比新的轴大的部分递归排序
QuickSort_Optimization(arr, gt + 1, hi);
}
}6. 堆排序
基本思想:堆对应一棵完全二叉树,且所有非叶结点的值均不大于(或不小于)其子女的值,根结点(堆顶元素)的值是最小(或最大)的,每次都取堆顶的元素,将其放在序列最后面,然后将剩余的元素重新调整为最小(大)堆,依次类推,最终得到排序的序列。
堆排序分为大顶堆和小顶堆排序。大顶堆:堆对应一棵完全二叉树,且所有非叶结点的值均不小于其子女的值,根结点(堆顶元素)的值是最大的。而小顶堆正好相反,小顶堆:堆对应一棵完全二叉树,且所有非叶结点的值均不大于其子女的值,根结点(堆顶元素)的值是最小的。
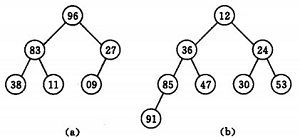
举个例子:
(a)大顶堆序列:(96, 83,27,38,11,09)
(b)小顶堆序列:(12,36,24,85,47,30,53,91)
实现堆排序需解决两个问题:
1. 如何将n 个待排序的数建成堆?
2. 输出堆顶元素后,怎样调整剩余n-1 个元素,使其成为一个新堆?
首先讨论第二个问题:输出堆顶元素后,怎样对剩余n-1元素重新建成堆?
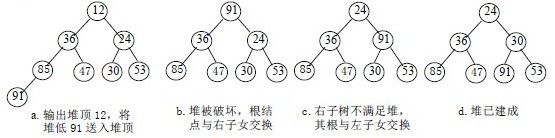
调整小顶堆的方法:
1)设有m 个元素的堆,输出堆顶元素后,剩下m-1 个元素。将堆底元素送入堆顶((最后一个元素与堆顶进行交换),堆被破坏,其原因仅是根结点不满足堆的性质。
2)将根结点与左、右子树中较小元素的进行交换。
3)若与左子树交换:如果左子树堆被破坏,即左子树的根结点不满足堆的性质,则重复方法 (2).
4)若与右子树交换,如果右子树堆被破坏,即右子树的根结点不满足堆的性质。则重复方法 (2).
5)继续对不满足堆性质的子树进行上述交换操作,直到叶子结点,堆被建成。
称这个自根结点到叶子结点的调整过程为筛选。如图:
再讨论第一个问题,如何将n 个待排序元素初始建堆?
建堆方法:对初始序列建堆的过程,就是一个反复进行筛选的过程。
1)n 个结点的完全二叉树,则最后一个结点是第n/2个结点的子树。
2)筛选从第n/2个结点为根的子树开始,该子树成为堆。
3)之后向前依次对各结点为根的子树进行筛选,使之成为堆,直到根结点。
如图建堆初始过程:无序序列:(49,38,65,97,76,13,27,49)
C#算法实现:
///
/// 堆排序
/// 堆对应一棵完全二叉树,且所有非叶结点的值均不大于(或不小于)其子女的值,根结点(堆顶元素)的值是最小(或最大)的
/// 每次都取堆顶的元素,将其放在序列最后面,然后将剩余的元素重新调整为最小堆,依次类推,最终得到排序的序列。
///
///
///
private static void HeapSort(int[] arr, int length)
{
CreateHeap(arr, length);
//从最后的节点进行调整
for (int i = length - 1; i > 0; i--)
{
//交换堆顶和最后一个节点的元素
Swap(ref arr[0], ref arr[i]);
//每次交换进行调整
AdjustHeap(arr, 0, i - 1);
}
}
///
/// 建堆方法:对初始序列建堆的过程,就是一个反复进行筛选的过程。
/// 1)n 个结点的完全二叉树,则最后一个结点是第n/2个结点的子树。
/// 2)筛选从第n/2个结点为根的子树开始,该子树成为堆。
/// 3)之后向前依次对各结点为根的子树进行筛选,使之成为堆,直到根结点。
/// 完全二叉树:除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少右边的若干结点。
///
private static void CreateHeap(int[] arr, int length)
{
for (int i = length / 2 - 1; i >= 0; i--)
{
AdjustHeap(arr, i, length - 1);
}
}
private static void AdjustHeap(int[] arr, int start, int length)
{
int root = start;
int child = root * 2 + 1;
while (child <= length)
{
//若子节点指标在范围内才做比较
if (child + 1 <= length && arr[child] < arr[child + 1])
{
//先比较两个子节点大小,选择最大的
child++;
}
//如果父节点大於子节点代表调整完毕,直接跳出函数
if (arr[root] > arr[child])
{
return;
}
else
{
//否则交换父子内容再继续子节点和孙节点比较
Swap(ref arr[root], ref arr[child]);
root = child;
child = root * 2 + 1;
}
}
}堆排序,还有一个扩展知识,二叉堆,对应一棵完全二叉树,且所有非叶结点的值均不大于(或不小于)其子女的值,根结点(堆顶元素)的值是最小(或最大)的。更多实现:C#数据结构-二叉堆实现
7. 归并排序
基本思想:将两个(或两个以上)有序表合并成一个新的有序表。
C#算法实现, 数组版本:
///
/// 归并排序 递归版本
/// 将两个(或两个以上)有序表合并成一个新的有序表
///
private static void MergeSort(int[] arr, int length)
{
int[] temp = new int[length];
MergeInternalSort(arr, 0, length, temp);
}
private static void MergeInternalSort(int[] arr, int first, int last, int[] temp)
{
if (first < last)
{
int mid = (first + last) / 2;
MergeInternalSort(arr, first, mid, temp);
MergeInternalSort(arr, mid + 1, last, temp);
Merge(arr, first, mid, last, temp);
}
}
private static void Merge(int[] arr, int first, int mid, int last, int[] temp)
{
int i = first;
int j = mid + 1;
int k = 0;
//通过比较,把较小的一部分数放入到temp数组中
while (i <= mid && j <= last)
{
if (arr[i] < arr[j])
{
temp[k++] = arr[i++];
}
else
{
temp[k++] = arr[j++];
}
}
//将数组剩余的数放入到temp数组中
while (i <= mid)
{
temp[k++] = arr[i++];
}
while (j <= last)
{
temp[k++] = arr[j++];
}
//把合并的数组结果赋值给原数组
for (int m = 0; m < k; m++)
{
arr[m + first] = temp[m];
}
}C#算法实现, List版本:
///
/// 归并排序 List版本
/// 将两个(或两个以上)有序表合并成一个新的有序表
///
public static List MergeSort(List list)
{
int count = list.Count;
if (count <= 1)
{
return list;
}
int mid = count / 2;
List left = new List();//定义左侧List
List right = new List();//定义右侧List
//以下两个循环把list分为左右两个List
for (int i = 0; i < mid; i++)
{
left.Add(list[i]);
}
for (int j = mid; j < count; j++)
{
right.Add(list[j]);
}
left = MergeSort(left);
right = MergeSort(right);
return Merge(left, right);
}
///
/// 合并两个已经排好序的List
///
/// 左侧List
/// 右侧List
/// Merge(List left, List right)
{
List temp = new List();
while (left.Count > 0 && right.Count > 0)
{
if (left[0] <= right[0])
{
temp.Add(left[0]);
left.RemoveAt(0);
}
else
{
temp.Add(right[0]);
right.RemoveAt(0);
}
}
if (left.Count > 0)
{
for (int i = 0; i < left.Count; i++)
{
temp.Add(left[i]);
}
}
if (right.Count > 0)
{
for (int i = 0; i < right.Count; i++)
{
temp.Add(right[i]);
}
}
return temp;
} 8. 桶排序
基本思想:类似于哈希表的拉链法,定义一个映射函数,将值放入对应的桶中,可以参考上文哈希查找。
C#算法实现:
///
/// 桶排序
/// 类似于哈希表的拉链法,定义一个映射函数,将值放入对应的桶中
/// 最坏时间情况:全部分到一个桶中O(N^2),一般情况为O(NlogN)
/// 最好时间情况:每个桶中只有一个数据时最优O(N)
/// int bucketNum = arr.Length;
/// 映射函数:int bucketIndex = arr[i] * bucketNum / (max + 1);
///
///
/// 数组的最大值
/// [] bucket = new LinkedList[arr.Length];
for (int i = 0; i < bucketNum; i++)
{
bucket[i] = new LinkedList();
}
// 元素分装各个桶中
for (int i = 0; i < bucketNum; i++)
{
//映射函数
int bucketIndex = arr[i] * bucketNum / (max + 1);
InsertIntoLinkList(bucket[bucketIndex], arr[i]);
}
// 从各个桶中获取后排序插入
int index = 0;
for (int i = 0; i < bucketNum; i++)
{
foreach (var item in bucket[i])
{
arr[index++] = item;
}
}
return arr;
}
///
/// 按升序插入 linklist
///
/// 要排序的链表
/// 要插入排序的数字
private static void InsertIntoLinkList(LinkedList linkedList, int num)
{
// 链表为空时,插入到第一位
if (linkedList.Count == 0)
{
linkedList.AddFirst(num);
return;
}
else
{
foreach (int i in linkedList)
{
if (i > num)
{
System.Collections.Generic.LinkedListNode node = linkedList.Find(i);
linkedList.AddBefore(node, num);
return;
}
}
linkedList.AddLast(num);
}
} 最后附上,测试用例代码:
static void Main(string[] args)
{
Console.WriteLine("冒泡排序:");
int[] arr = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
BubbleSort(arr, arr.Length);
Show(arr);
Console.WriteLine("\n选择排序:");
int[] temp1 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
SelectSort(temp1, temp1.Length);
Show(temp1);
Console.WriteLine("\n快速排序:");
int[] temp2 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
QuickSort(temp2, 0, temp2.Length - 1);
Show(temp2);
Console.WriteLine("\n快速排序优化:");
int[] temp8 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5, 5, 5, 5, 5 };
QuickSort_Optimization(temp8, 0, temp8.Length - 1);
Show(temp8);
Console.WriteLine("\n插入排序:");
int[] temp3 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
InsertionSort(temp3, temp3.Length);
Show(temp3);
Console.WriteLine("\n希尔排序:");
int[] temp4 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
ShellSort(temp4, temp4.Length);
Show(temp4);
Console.WriteLine("\n堆排序:");
int[] temp5 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
HeapSort(temp5, temp5.Length);
Show(temp5);
Console.WriteLine("\n归并排序:");
int[] temp6 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
MergeSort(temp6, temp6.Length);
Show(temp6);
Console.WriteLine("\n桶排序:");
int[] temp7 = { 1, 3, 4, 6, 9, 10, 32, 45, 2, 5 };
//注:这里后两个参数传入的是数组的最大值,最小值
BucketSort(temp7, 45, 1);
Show(temp7);
Console.ReadLine();
}
private static void Show(int[] arr)
{
int length = arr.Length;
for (int i = 0; i < length; i++)
{
Console.Write(arr[i] + " ");
}
}执行结果:
(1)当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O(n);
(2)而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O(n^2);
(3)原表是否有序,对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
每种排序算法都各有优缺点。因此,在实用时需根据不同情况适当选用,甚至可以将多种方法结合起来使用。
选择排序算法的依据:
影响排序的因素有很多,平均时间复杂度低的算法并不一定就是最优的。相反,有时平均时间复杂度高的算法可能更适合某些特殊情况。同时,选择算法时还得考虑它的可读性,以利于软件的维护。一般而言,需要考虑的因素有以下四点:
(1)待排序的记录数目n的大小;
(2)记录本身数据量的大小,也就是记录中除关键字外的其他信息量的大小;
(3)关键字的结构及其分布情况;
(4)对排序稳定性的要求。
设待排序元素的个数为n.
(1)当n较大,则应采用时间复杂度为O(n*logn)的排序方法:快速排序、堆排序或归并排序。
快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
堆排序:如果内存空间允许且要求稳定性的;
归并排序:它有一定数量的数据移动,所以我们可能过与插入排序组合,先获得一定长度的序列,然后再合并,在效率上将有所提高。
(2)当n较大,内存空间允许,且要求稳定性:归并排序
(3)当n较小,可采用直接插入或直接选择排序。
直接插入排序:当元素分布有序,直接插入排序将大大减少比较次数和移动记录的次数。
直接选择排序:当元素分布有序,如果不要求稳定性,选择直接选择排序。
(4)一般不使用或不直接使用传统的冒泡排序。
最后附上,旧金山大学计算机系的一个网站,可以用非常形象的动画展示,各种排序算法的执行过程,超链接地址
除了以上这些排序算法,其实还有很多其他的算法,比如C#List的排序,内省排序:
-
如果分区大小少于16个元素,则使用插入排序算法。
-
如果分区数量超过2 * LogN,其中N是输入数组的范围,则它使用Heapsort算法。
-
否则,它使用Quicksort算法。
附上:前辈大神的博客,更详细的算法细节,可以参考。
[Data Structure & Algorithm] 八大排序算法
【经典排序算法】八大排序对比总结