常用滤波器Matlab程序设计
常用滤波器Matlab程序设计
(低通滤波器、高通滤波器、带通滤波器、带阻滤波器)
以下四个滤波器都是切比雪夫I型数字滤波器
1.低通滤波器
低通滤波(Low-pass filter) 是一种过滤方式,规则为低频信号能正常通过,而超过设定临界值的高频信号则被阻隔、减弱。但是阻隔、减弱的幅度则会依据不同的频率以及不同的滤波程序(目的)而改变。它有的时候也被叫做高频去除过滤(high-cut filter)或者最高去除过滤(treble-cut filter)。低通过滤是高通过滤的对立。
低通滤波
低通滤波可以简单的认为:设定一个频率点,当信号频率高于这个频率时不能通过,在数字信号中,这个频率点也就是截止频率,当频域高于这个截止频率时,则全部赋值为0。因为在这一处理过程中,让低频信号全部通过,所以称为低通滤波。
低通过滤的概念存在于各种不同的领域,诸如电子电路,数据平滑,声学阻挡,图像模糊等领域经常会用到。
在数字图像处理领域,从频域看,低通滤波可以对图像进行平滑去噪处理。
低通滤波器
对于不同滤波器而言,每个频率的信号的减弱程度不同。当使用在音频应用时,它有时被称为高频剪切滤波器,或高音消除滤波器。
低通滤波器概念有许多不同的形式,其中包括电子线路(如音频设备中使用的hiss 滤波器、平滑数据的数字算法、音障(acoustic barriers)、图像模糊处理等等,这两个工具都通过剔除短期波动、保留长期发展趋势提供了信号的平滑形式。低通滤波器在信号处理中的作用等同于其它领域如金融领域中移动平均数(moving average)所起的作用;低通滤波器有很多种。其中,最通用的就是巴特沃斯滤波器和切比雪夫滤波器。
接下来用Matlab程序设计低通滤波器生成m文件如下:
function y=lowp(x,f1,f3,rp,rs,Fs)
%低通滤波
%使用注意事项:通带或阻带的截止频率的选取范围是不能超过采样率的一半
%即,f1,f3的值都要小于 Fs/2
%x:需要带通滤波的序列
% f 1:通带截止频率
% f 3:阻带截止频率
%rp:边带区衰减DB数设置
%rs:截止区衰减DB数设置
%Fs:序列x的采样频率
wp=2*pi*f1/Fs;
ws=2*pi*f3/Fs;
% 设计切比雪夫滤波器;
[n,wn]=cheb1ord(wp/pi,ws/pi,rp,rs);
[bz1,az1]=cheby1(n,rp,wp/pi);
%查看设计滤波器的曲线
[h,w]=freqz(bz1,az1,256,Fs);
h=20*log10(abs(h));
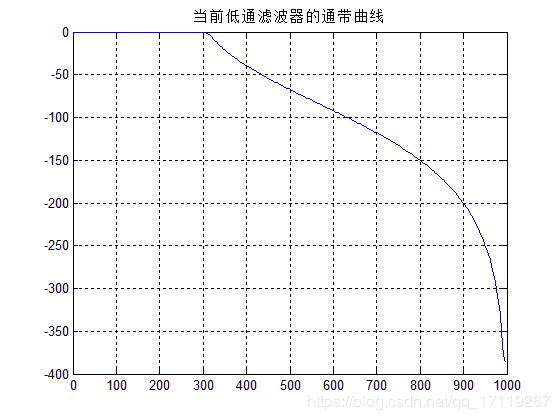
figure;plot(w,h);title('当前低通滤波器的通带曲线');grid on;
y=filter(bz1,az1,x);%对序列x滤波后得到的序列y
end
为了方便起见,专门封装专门画频谱图的函数,函数名plot_fft。后边所有绘制有关函数频谱图将会直接调用,为避免函数调用出现问题,此函数生产m文件保存到程序运行当前文件夹下。以下是plot_fft函数设计实现。
%画信号的幅频谱和功率谱
function plot_fft(y,fs,style,varargin)
%当style=1,画幅值谱;当style=2,画功率谱;当style=其他的,那么花幅值谱和功率谱
%当style=1时,还可以多输入2个可选参数
%可选输入参数是用来控制需要查看的频率段的
%第一个是需要查看的频率段起点
%第二个是需要查看的频率段的终点
%其他style不具备可选输入参数,如果输入发生位置错误
nfft=2^nextpow2(length(y));%找出大于y的个数的最大的2的指数值(自动进算最佳FFT步长nfft)
%nfft=1024;%人为设置FFT的步长nfft
y=y-mean(y);%去除直流分量
y_ft=fft(y,nfft);%对y信号进行DFT,得到频率的幅值分布
y_p=y_ft.*conj(y_ft)/nfft;%conj()函数是求y函数的共轭复数,实数的共轭复数是他本身。
y_f=fs*(0:nfft/2-1)/nfft;%T变换后对应的频率的序列
% y_p=y_ft.*conj(y_ft)/nfft;%conj()函数是求y函数的共轭复数,实数的共轭复数是他本身。
if style==1
if nargin==3
%plot(y_f,abs(y_ft(1:nfft/2)));%论坛上画FFT的方法
plot(y_f,2*abs(y_ft(1:nfft/2))/length(y));%matlab的帮助里画FFT的方法
ylabel('幅值');xlabel('频率');title('信号幅值谱');
else
f1=varargin{1};
fn=varargin{2};
ni=round(f1 * nfft/fs+1);
na=round(fn * nfft/fs+1);
plot(y_f(ni:na),abs(y_ft(ni:na)*2/nfft));
ylabel('幅值');xlabel('频率');title('信号幅值谱');
end
elseif style==2
plot(y_f,y_p(1:nfft/2));
ylabel('功率谱密度');xlabel('频率');title('信号功率谱');
else
subplot(211);plot(y_f,2*abs(y_ft(1:nfft/2))/length(y));
ylabel('幅值');xlabel('频率');title('信号幅值谱');
subplot(212);plot(y_f,y_p(1:nfft/2));
ylabel('功率谱密度');xlabel('频率');title('信号功率谱');
end
end
低通滤波器案例设计:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%低通滤波器案例设计
clear all; clc; close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% rp=0.1;rs=20;%通带边衰减DB值和阻带边衰减DB值(根据实际情况设定参数此为测试默认值)
% Fs=2000;%采样率
fs=2000;%采样频率
t=(1:fs)/fs;%采样时间
ff1=100;%信号频率100,400
ff2=400;
x=sin(2*pi*ff1*t)+sin(2*pi*ff2*t);%带测试的x序列
figure;
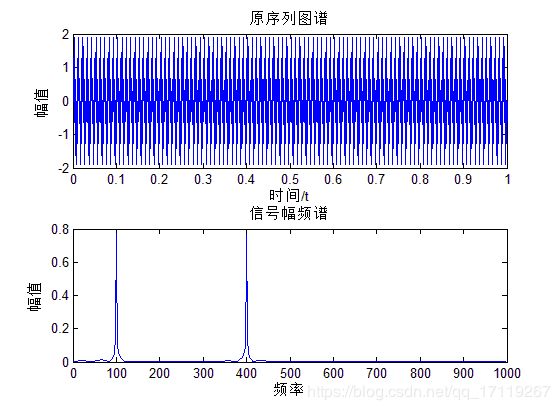
subplot(211);plot(t,x);%原序列图象。
subplot(212);plot_fft(x,fs,1);%原图像对应频谱
%低通测试
% y=filter(bz1,az1,x);
y=lowp(x,300,350,0.1,20,fs);%低通滤波器函数测试。
figure;
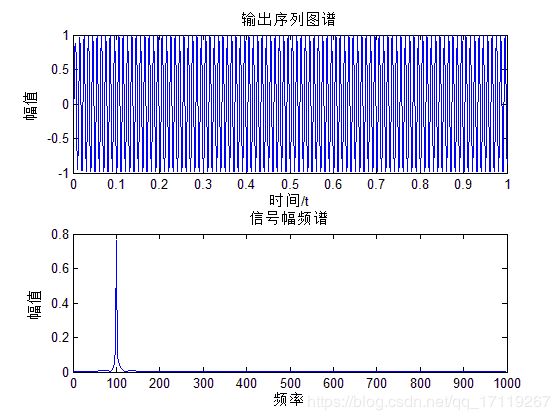
subplot(211);plot(t,y);%低通滤波器输出序列
subplot(212);plot_fft(y,fs,1);%低通滤波器输出序列对应频谱
%plot_fft()函数已在上面给出主需要调用即可。
总结:
通过简单测试,以上三幅图分别是滤波前后的时频图,滤波器的滤波特性曲线图。通过图可以看出低通滤波器成功留下了100Hz的低频成分而把不要的高频成分去除了。实现低通滤波器基本功能。
2.高通滤波器
高通滤波(high-pass filter) 是一种过滤方式,规则为高频信号能正常通过,而低于设定临界值的低频信号则被阻隔、减弱。但是阻隔、减弱的幅度则会依据不同的频率以及不同的滤波程序(目的)而改变。它有的时候也被叫做低频去除过滤(low-cut filter)。高通滤波是低通滤波的对立。
高通滤波
高通滤波是只对低于某一给定频率以下的频率成分有衰减作用,而允许这个截频以上的频率成分通过,并且没有相位移的滤波过程。主要用来消除低频噪声,也称低截止滤波器。
高通滤波属于[频率域]滤波,它保留高频,抑制低频,是[图像锐化]的一种方式。
高通滤波器
高通滤波器是一种让某一频率以上的信号分量通过,而对该频率以下的信号分量大大抑制的电容、电感与电阻等器件的组合装置。其特性在时域及频域中可分别用冲激响应及频率响应描述。后者是用以频率为自变量的函数表示,一般情况下它是一个以复变量jω为自变量的的复变函数,以H(jω)表示。它的模H(ω)和幅角φ(ω)为角频率ω的函数,分别称为系统的“幅频响应”和“相频响应”,它分别代表激励源中不同频率的信号成分通过该系统时所遇到的幅度变化和相位变化。可以证明,系统的“频率响应”就是该系统“冲激响应”的傅里叶变换。当线性无源系统可以用一个N阶线性微分方程表示时,频率响应H(jω)为一个有理分式,它的分子和分母分别与微分方程的右边和左边相对应。
接下来用Matlab程序设计高通滤波器生成m文件如下:
function y=highp(x,f1,f3,rp,rs,Fs)
%高通滤波
%使用注意事项:通带或阻带的截止频率的选取范围是不能超过采样率的一半
%即,f1,f3的值都要小于 Fs/2
%x:需要带通滤波的序列
% f 1:通带截止频率
% f 2:阻带截止频率
%rp:边带区衰减DB数设置
%rs:截止区衰减DB数设置
%Fs:序列x的采样频率
wp=2*pi*f1/Fs;
ws=2*pi*f3/Fs;
% 设计切比雪夫滤波器;
[n,wn]=cheb1ord(wp/pi,ws/pi,rp,rs);
[bz1,az1]=cheby1(n,rp,wp/pi,'high');
%查看设计滤波器的曲线
[h,w]=freqz(bz1,az1,256,Fs);
h=20*log10(abs(h));
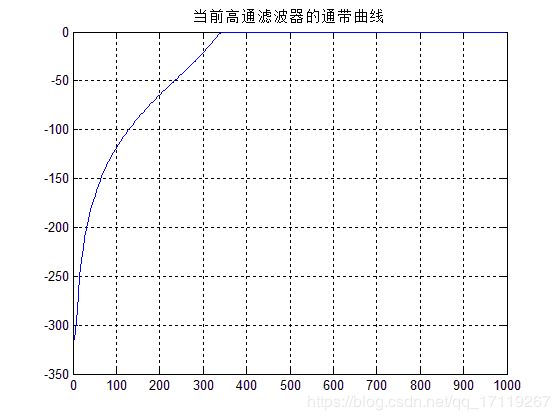
figure;plot(w,h);title('当前高通滤波器的通带曲线');grid on;
y=filter(bz1,az1,x);
end
高通滤波器案例设计:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%高通滤波器案例设计测试程序
clear all; clc; close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fs=2000;%采样频率
t=(1:fs)/fs;%采样时间
ff1=100;%信号频率100,400
ff2=400;
x=sin(2*pi*ff1*t)+sin(2*pi*ff2*t);%带测试的x序列
figure;
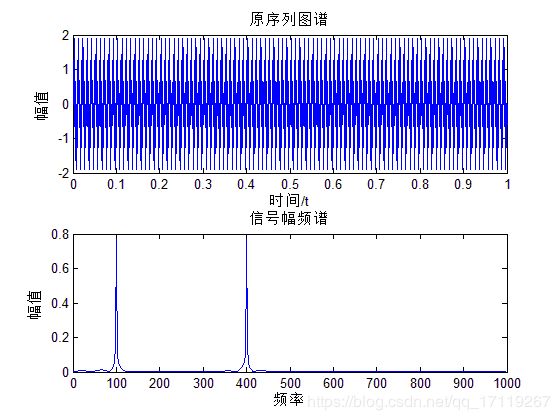
subplot(211);plot(t,x);%原序列图谱。
subplot(212);plot_fft(x,fs,1);%原图像对应频谱
%高通测试
z=highp(x,350,300,0.1,20,fs);%高通滤波器函数测试。
figure;
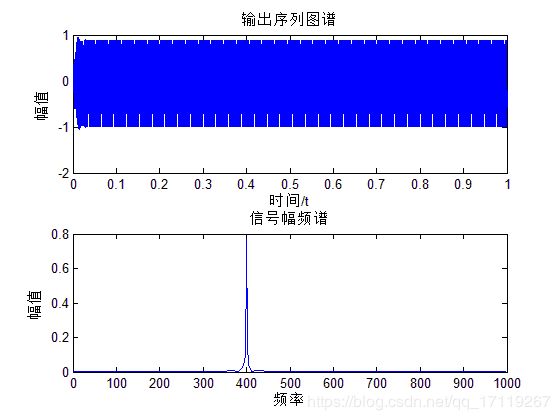
subplot(211);plot(t,z);%高通滤波器输出序列图谱
subplot(212);plot_fft(z,fs,1);%高通滤波器输出序列对应频谱
总结:
通过简单测试,以上三幅图分别是滤波前后的时频图,滤波器的滤波特性曲线图。通过图可以看出高通滤波器成功留下了400Hz的高频成分而把不要的低频成分去除了。实现高通滤波器基本功能。
3.带通滤波器
带通滤波器(band-pass filter)是一个允许特定频段的波通过同时屏蔽其他频段的设备。比如RLC振荡回路就是一个模拟带通滤波器。
定义:
带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器,与带阻滤波器的概念相对。一个模拟带通滤波器的例子是电阻-电感-电容电路(RLC circuit)。这些滤波器也可以用低通滤波器同高通滤波器组合来产生。
工作原理:
一个理想的带通滤波器应该有一个完全平坦的通带,在通带内没有放大或者衰减,并且在通带之外所有频率都被完全衰减掉,另外,通带外的转换在极小的频率范围完成。
实际上,并不存在理想的带通滤波器。滤波器并不能够将期望频率范围外的所有频率完全衰减掉,尤其是在所要的通带外还有一个被衰减但是没有被隔离的范围。这通常称为滤波器的滚降现象,并且使用每十倍频的衰减幅度的dB数来表示。通常,滤波器的设计尽量保证滚降范围越窄越好,这样滤波器的性能就与设计更加接近。然而,随着滚降范围越来越小,通带就变得不再平坦,开始出现“波纹”。这种现象在通带的边缘处尤其明显,这种效应称为吉布斯现象。
在频带较低的剪切频率f1和较高的剪切频率f2之间是共振频率,这里滤波器的增益最大,滤波器的带宽就是f2和f1之间的差值。
接下来用Matlab程序设计带通滤波器生成m文件如下:
function y=bandp(x,f1,f3,fsl,fsh,rp,rs,Fs)
%带通滤波
%使用注意事项:通带或阻带的截止频率与采样率的选取范围是不能超过采样率的一半
%即,f1,f3,fs1,fsh,的值小于 Fs/2
%x:需要带通滤波的序列
% f 1:通带左边界
% f 3:通带右边界
% fs1:衰减截止左边界
% fsh:衰变截止右边界
%rp:边带区衰减DB数设置
%rs:截止区衰减DB数设置
%Fs:序列x的采样频率
wp1=2*pi*f1/Fs;
wp3=2*pi*f3/Fs;
wsl=2*pi*fsl/Fs;
wsh=2*pi*fsh/Fs;
wp=[wp1 wp3];
ws=[wsl wsh];
% 设计切比雪夫滤波器;
[n,wn]=cheb1ord(ws/pi,wp/pi,rp,rs);
[bz1,az1]=cheby1(n,rp,wp/pi);
%查看设计滤波器的曲线
[h,w]=freqz(bz1,az1,256,Fs);
h=20*log10(abs(h));
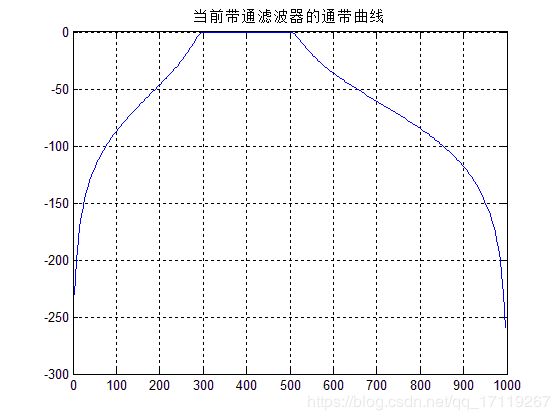
figure;plot(w,h);title('所设计滤波器的通带曲线');grid on;
y=filter(bz1,az1,x);
end
带通滤波器案例设计:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%带通滤波器案例设计测试程序
clear all; clc; close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% f1=300;f3=500;%通带截止频率上下限
% fsl=200;fsh=600;%阻带截止频率上下限
% rp=0.1;rs=30;%通带边衰减DB值和阻带边衰减DB值
% Fs=2000;%采样率
fs=2000;%采样频率
t=(1:fs)/fs;%采样时间
ff1=100;%信号频率100,400,700
ff2=400;
ff3=700;
x=sin(2*pi*ff1*t)+sin(2*pi*ff2*t)+sin(2*pi*ff3*t);%带测试的x序列
figure;
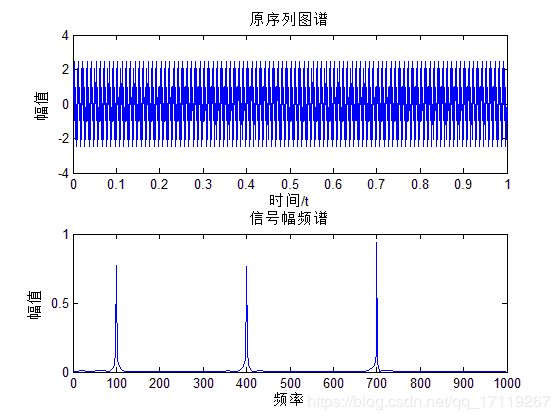
subplot(211);plot(t,x);%原序列图谱。
subplot(212);plot_fft(x,fs,1);%原图像对应频谱
% y=filter(bz1,az1,x);
%带通测试
y=bandp(x,300,500,200,600,0.1,30,fs);%带通滤波器函数测试。
figure;
subplot(211);plot(t,y);%带通滤波器输出序列图谱
subplot(212);plot_fft(y,fs,1);%带通滤波器输出序列对应频谱
总结:
通过简单测试,以上三幅图分别是滤波前后的时频图,滤波器的滤波特性曲线图。通过图可以看出带通滤波器成功留下了400Hz的带通频带内成分而把不要的频带成分去除了。实现带通滤波器基本功能。
4.带阻滤波器
带阻滤波器(bandstop filters,简称BSF)是指能通过大多数频率分量、但将某些范围的频率分量衰减到极低水平的滤波器,与带通滤波器的概念相对。其中点阻滤波器(notch filter)是一种特殊的带阻滤波器,它的阻带范围极小,有着很高的Q值(Q Factor)。
定义:
在电路中将输入电压同时作用于低通滤波器和高通滤波器,再将两个电路的输出电压求和,就可以得到带阻滤波器。带阻滤波器一般分为腔体带阻滤波器和LC带阻滤波器。
接下来用Matlab程序设计带阻滤波器生成m文件如下:
function y=bands(x,f1,f3,fsl,fsh,rp,rs,Fs)
%带阻滤波
%使用注意事项:通带或阻带的截止频率与采样率的选取范围是不能超过采样率的一半
%即,f1,f3,fs1,fsh,的值小于 Fs/2
%x:需要带通滤波的序列
% f 1:通带左边界
% f 3:通带右边界
% fs1:衰减截止左边界
% fsh:衰变截止右边界
%rp:边带区衰减DB数设置
%rs:截止区衰减DB数设置
%FS:序列x的采样频率
wp1=2*pi*f1/Fs;
wp3=2*pi*f3/Fs;
wsl=2*pi*fsl/Fs;
wsh=2*pi*fsh/Fs;
wp=[wp1 wp3];
ws=[wsl wsh];
% 设计切比雪夫滤波器;
[n,wn]=cheb1ord(ws/pi,wp/pi,rp,rs);
[bz1,az1]=cheby1(n,rp,wp/pi,'stop');
%查看设计滤波器的曲线
[h,w]=freqz(bz1,az1,256,Fs);
h=20*log10(abs(h));
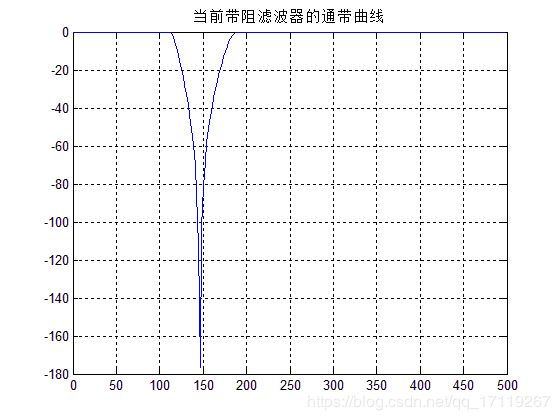
figure;plot(w,h);title('所设计滤波器的通带曲线');grid on;
y=filter(bz1,az1,x);
end
带阻滤波器案例设计:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%带阻滤波器案例设计测试程序
clear all; clc; close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% f1=300;f3=500;%通带截止频率上下限
% fsl=200;fsh=600;%阻带截止频率上下限
% rp=0.1;rs=30;%通带边衰减DB值和阻带边衰减DB值
% Fs=2000;%采样率
fs=1000;%采样频率
t=(1:fs)/fs;%采样时间
ff1=100;%信号频率100,400,700
ff2=150;
ff3=200;
x=sin(2*pi*ff1*t)+sin(2*pi*ff2*t)+sin(2*pi*ff3*t);%带测试的x序列
figure;
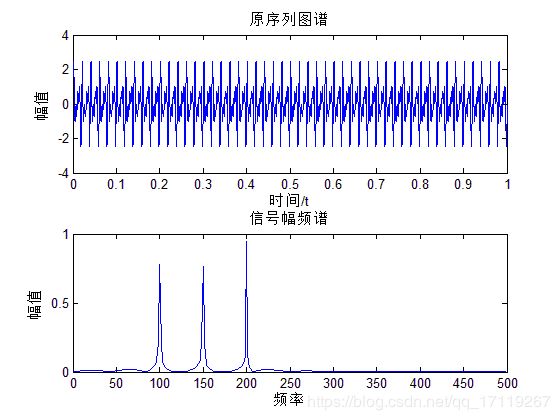
subplot(211);plot(t,x);%原序列图谱。
subplot(212);plot_fft(x,fs,1);%原图像对应频谱
%带通测试
y=bands(x,110,190,140,160,0.1,30,fs);%带通滤波器函数测试。
figure;
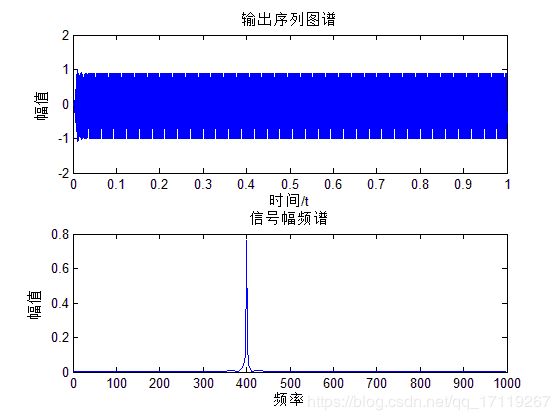
subplot(211);plot(t,y);%带通滤波器输出序列图谱
subplot(212);plot_fft(y,fs,1);%带通滤波器输出序列对应频谱
总结:
通过简单测试,以上三幅图分别是滤波前后的时频图,滤波器的滤波特性曲线图。通过图可以看出带通滤波器成功去除了150Hz的带通频带内成分而把需要的频带成分留下来。实现带阻滤波器基本功能。