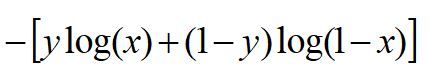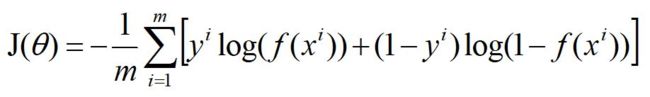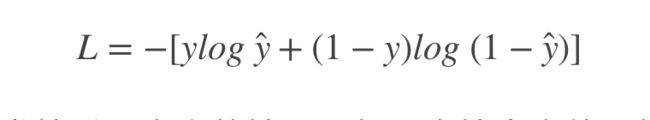NLP面试题目21-25

21.LR和SVM的联系与区别？

联系：
1、LR和SVM都可以处理分类问题，且一般都用于处理线性二分类问题（在改进的情况下可以处理多分类问题）
2、两个方法都可以增加不同的正则化项，如L1、L2等等。所以在很多实验中，两种算法的结果是很接近的。
区别：
1、LR是参数模型，SVM是非参数模型。
2、从目标函数来看，区别在于逻辑回归采用的是Logistical Loss，SVM采用的是hinge loss.这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。
3、SVM的处理方法是只考虑Support Vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。
4、逻辑回归相对来说模型更简单，好理解，特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些，SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
5、Logic 能做的 SVM能做，但可能在准确率上有问题，SVM能做的Logic有的做不了。

22.LR与线性回归的区别与联系？

个人感觉逻辑回归和线性回归首先都是广义的线性回归，
其次经典线性模型的优化目标函数是最小二乘，而逻辑回归则是似然函数，
另外线性回归在整个实数域范围内进行预测，敏感度一致，而分类范围，需要在[0,1]。逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型，因而对于这类问题来说，逻辑回归的鲁棒性比线性回归的要好。
逻辑回归的模型本质上是一个线性回归模型，逻辑回归都是以线性回归为理论支持的。但线性回归模型无法做到sigmoid的非线性形式，sigmoid可以轻松处理0/1分类问题。

23.L1和L2的区别。

L1范数（L1 norm）是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）。
比如 向量A=[1，-1，3]， 那么A的L1范数为 |1|+|-1|+|3|.
简单总结一下就是：
L1范数: 为x向量各个元素绝对值之和。
L2范数: 为x向量各个元素平方和的1/2次方，L2范数又称Euclidean范数或Frobenius范数

Lp范数: 为x向量各个元素绝对值p次方和的1/p次方.
在支持向量机学习过程中，L1范数实际是一种对于成本函数求解最优的过程，因此，L1范数正则化通过向成本函数中添加L1范数，使得学习得到的结果满足稀疏化，从而方便人类提取特征。
L1范数可以使权值稀疏，方便特征提取。
L2范数可以防止过拟合，提升模型的泛化能力。

---

1）L1范式是对应参数向量绝对值之和

（2）L1范式具有稀疏性

（3）L1范式可以用来作为特征选择，并且可解释性较强（这里的原理是在实际Loss function中都需要求最小值，根据L1的定义可知L1最小值只有0，故可以通过这种方式来进行特征选择）

（4）L2范式是对应参数向量的平方和，再求平方根

（5）L2范式是为了防止机器学习的过拟合，提升模型的泛化能力

---

15.L1和L2正则先验分别服从什么分布 ？

@齐同学：面试中遇到的，L1和L2正则先验分别服从什么分布，L1是拉普拉斯分布，L2是高斯分布。

24.SVM的模型的推导

25.LR的原理和Loss的推导

前面的线性回归，我们已经得到y=wx+b。它是实数，y的取值范围可以是（负无穷，正无穷）。现在，我们不想让它的值这么大，所以我们就想把这个值给压缩一下，压缩到[0,1]。什么函数可以干这个事呢？研究人员发现signomid函数就有这个功能。
sigmoid的函数如下：

压缩，就是把y=wx+b带入sigmoid(x)。把这个函数的输出，还定义为y,即：

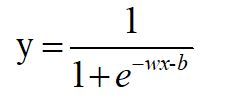
把这个式子变换一下：

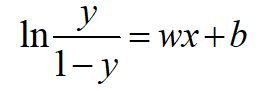
损失函数

以二分类（0，1）为例：

当真值为1，模型的预测输出为1时，损失最好为0，预测为0是，损失尽量大。

同样的，当真值为0，模型的预测输出为0时，损失最好为0，预测为1是，损失尽量大。

这个损失函数为：

我们把这两个损失综合起来：

对于m个样本，总的损失：

25.5 线性回归损失函数

对于训练数据样本(xi,yi)，我们有如下的拟合直线：

我们构建了一个损失函数：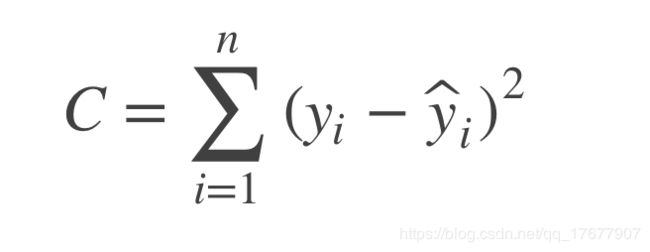

损失函数为什么要用平方差形式呢？

简单的说，是因为使用平方形式的时候，使用的是“最小二乘法”的思想，这里的“二乘”指的是用平方来度量观测点与估计点的距离（远近），“最小”指的是参数值要保证各个观测点与估计点的距离的平方和达到最小。
假设观测输出与预估数据之间的误差符合正太分布

25.6 SVM损失函数

25.7 朴素贝叶斯

参考链接

25.8 交叉熵损失函数