LeetCode刷题(十)----数组-----medium部分(Java、C++)
LeetCode刷题(十)-----数组-------medium部分(Java、C++)
238. 除自身以外数组的乘积
给定长度为n的整数数组nums,其中n>1,返回输出数组output,其中output[i]等于nums中除nums[i]之外其余各元素的乘积。
示例:
输入: [1,2,3,4]
输出: [24,12,8,6]
说明:请不要使用除法,且在O(n)时间复杂度内完成此题。
进阶:你可以在常数空间复杂度内完成这个题目吗?(出于对空间复杂度分析的目的,输出数组不被视为额外空间。)
思路一:

链接:https://leetcode-cn.com/problems/product-of-array-except-self/solution/cheng-ji-dang-qian-shu-zuo-bian-de-cheng-ji-dang-q/
思路二:
链接:https://leetcode-cn.com/problems/product-of-array-except-self/comments/59944/
C++ 左右累乘,巧妙记录每个元素的左右乘积,时间复杂度O(n),空间复杂度0(1)。

我的:
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums)
{
int n = nums.size();
int left = 1;
int right = 1;
vector<int> res(n,1);
for(int i=0; i< n;i++)
{
res[i] *= left;
left = left * nums[i];
res[n-i-1] *= right;
right *= nums[n-i-1];
}
return res;
}
};
105. 从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:

我的:
第一部分:

从图中看出的最重要的一点是前序序列怎末划分成两部分。其实可以先在中序中找出左边有n个元素,然后前序除了第一个头节点之后的n个元素就是左子树上的前序序列。另外的就是右子树的前序序列。 注意上图中前序中序分块的颜色匹配。
第二部分:
根据前序和中序可以构造一颗二叉树,根据中序和后续也可以构建一颗二叉树。反正必须要有中序才能构建,因为没有中序,你没办法确定树的形状。比如先序和后序是不能构建唯一的一颗二叉树的。
因为先序先遍历根节点,可以确定根节点为 3; 再根据中序得到: leftInOrder = [9] RightInOrder = [15, 20 ,7] 又由于中序和先序的数组大小应该相同的, 所以, LeftPreOrder = [9] RightPreOrder = [20, 15, 7] 至此,划分为子问题: leftInOrder = [9] LeftPreOrder = [9] 构建左子树。 RightPreOrder = [20, 15, 7] RightInOrder = [15, 20 ,7] 构建右子树。
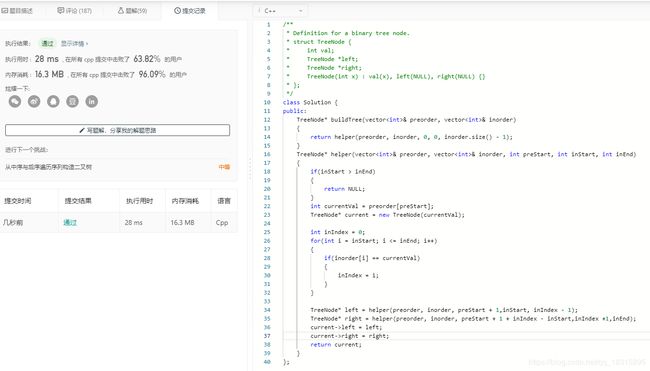
程序:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
return helper(preorder, inorder, 0, 0, inorder.size() - 1);
}
TreeNode* helper(vector<int>& preorder, vector<int>& inorder, int preStart, int inStart, int inEnd)
{
if(inStart > inEnd)
{
return NULL;
}
int currentVal = preorder[preStart];
TreeNode* current = new TreeNode(currentVal);
int inIndex = 0;
for(int i = inStart; i <= inEnd; i++)
{
if(inorder[i] == currentVal)
{
inIndex = i;
}
}
TreeNode* left = helper(preorder, inorder, preStart + 1,inStart, inIndex - 1);
TreeNode* right = helper(preorder, inorder, preStart + 1 + inIndex - inStart,inIndex +1,inEnd);
current->left = left;
current->right = right;
return current;
}
};
参考链接:https://www.v2ex.com/amp/t/541001
https://blog.51cto.com/f1yinsky/2373666?source=dra
287.寻找重复数
给定一个包含n+1个整数的数组nums,其数字都在 1 到 n 之间(包括1 和n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: [1,3,4,2,2]
输出: 2
示例 2:
输入: [3,1,3,4,2]
输出: 3
说明:
- 不能更改原数组(假设数组是只读的)。
- 只能使用额外的 O(1) 的空间。
- 时间复杂度小于 O(n2) 。
- 数组中只有一个重复的数字,但它可能不止重复出现一次。
思路一:
注释 :
前面的两种方法不满足提示中给出的约束条件,但它们是您在技术面试中可能会想到的解决方案。作为一名面试官,我个人不希望有人提出循环解决方案。
证明:
证明 nums 中存在至少一个副本是鸽子洞原理的简单应用。这里,nums 中的每个数字都是一个 “鸽子”,nums 中可以出现的每个不同的数字都是一个 “鸽子洞”。因为有n+1 个数是 nn 个不同的可能数,鸽子洞原理意味着至少有一个数是重复的。
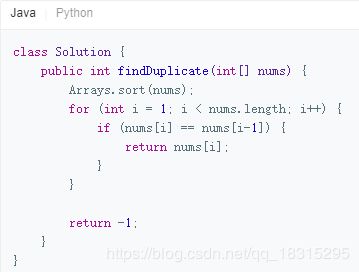
方法一:排序
如果对数字进行排序,则任何重复的数字都将与排序后的数组相邻。
算法:
算法相当简单。首先,我们对数组进行排序,然后将每个元素与前一个元素进行比较。因为数组中只有一个重复的元素,所以我们知道数组的长度至少为 2,一旦找到重复的元素,我们就可以返回它。
复杂度分析
时间复杂度: O(nlgn)。排序调用在 Python 和 Java 中花费 O(nlgn) 时间,因此它支配后续的线性扫描。
空间复杂度:O(1) (or O(n)),在这里,我们对 nums 进行排序,因此内存大小是恒定的。如果我们不能修改输入数组,那么我们必须为 nums 的副本分配线性空间,并对其进行排序。
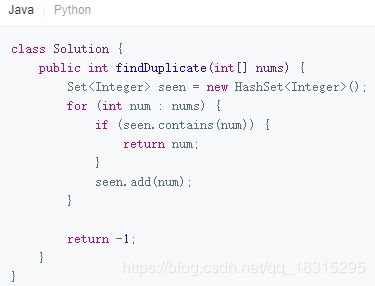
方法二:集合
如果我们在数组上迭代时存储每个元素,我们可以在数组上迭代时简单地检查每个元素。
算法:
为了实现线性时间复杂性,我们需要能够在恒定时间内将元素插入数据结构(并查找它们)。set 很好地满足这些约束,所以我们迭代数组并将每个元素插入 seen 中。在插入之前,我们检查它是否已经存在。如果是,那么我们找到了我们的副本,所以我们返回它。
复杂度分析
时间复杂度:O(n)。Python 和 Java 都依赖于底层的哈希表,所以插入和查找有固定的时间复杂度。因此,该算法是线性的,因为它由一个执行 NN 次恒定工作的 for 循环组成。
空间复杂度:O(n),在最坏的情况下,重复元素出现两次,其中一次出现在数组索引 n-1处。在这种情况下,seen 将包含 n-1不同的值,因此将占用 O(n)空间。
作者:LeetCode
链接:https://leetcode-cn.com/problems/find-the-duplicate-number/solution/xun-zhao-zhong-fu-shu-by-leetcode/
思路二:使用二分法在候选区间里定位目标数值(C++、Java、Python)
思路分析:
如果题目不限制:
1、不能更改原数组(假设数组是只读的);
2、只能使用额外的 O(1) 的空间。
容易想到的方法有:
(1)使用哈希表判重,这违反了限制 2;
(2)排序以后,重复的数相邻,这违反了限制 1;
(3)使用“抽屉原理”,当两个数发现要放在同一个地方的时候,就发现了这个重复的元素,这违反了限制 1;
(4)既然要定位数,可以对“数”做二分,但是比较恶心的一点是得反复看整个数组好几次,于是就有下面的二分法,本文就介绍通过二分法定位数;
(5)还可以使用“快慢指针”来完成,不过这种做法太有技巧性了,不是通用的做法,大家可以在评论区和题解区看到。
方法:二分法
关键:这道题的关键是对要定位的“数”做二分,而不是对数组的索引做二分。要定位的“数”根据题意在1和n之间,每一次二分都可以将搜索区间缩小一半。
以[1,2,2,3,4,5,6,7]为例,一共有8个数,每个数都在1和7之间。1和 7的中位数是4,遍历整个数组,统计小于4 的整数的个数,至多应该为3个,如果超过3个就说明重复的数存在于区间[1,4)(注意:左闭右开)中;否则,重复的数存在于区间 [4,7](注意:左右都是闭)中。这里小于 4的整数有4个(它们是 1, 2, 2, 3),因此砍掉右半区间,连中位数也砍掉。以此类推,最后区间越来越小,直到变成 1个整数,这个整数就是我们要找的重复的数。
参考代码1:

说明:1、在 Python 中,整除使用 // ,如果使用 / ,在不能整除的时候,会返回一个小数;
2、之所以写成 mid = left + (right - left + 1) // 2 ,是因为下面的分支条件是:left = mid 和 right = mid - 1,如果写成 mid = left + (right - left) // 2 就会陷入死循环。我们还是以具体例子为例。
当一个整数数组(按升序排列)的个数为奇数时,不论 mid = left + (right - left)//2和mid=left+(right-left+1) // 2都落在了相同的一个数,大家不妨拿 [1,2,3,4,5] 做验证;
当一个整数数组(按升序排列)的个数为偶数时:
(1) mid = left + (right - left) // 2 找到的是中间位置偏左的元素;
(2) mid = left + (right - left + 1) // 2 找到的是中间位置偏右的元素。
可以拿 [1,2,3,4] 验证。
因此如果分支是:left = mid 和 right = mid - 1,说明,当只有 2 个元素的时候,中位数不能取左边,否则会出现死循环,因此中位数的取法是 mid = left + (right - left + 1) // 2。
如果分支是:left = mid + 1 和 right = mid,说明,当只有 2 个元素的时候,中位数不能取右边,否则会出现死循环,因此中位数的取法是 mid = left + (right - left) // 2。
3、while left < right 一定是严格小于,这样退出循环的时候就一定有 l==r 成立,就不必纠结该返回 l 还是 r 了。
总结一下:while left < right 一定是严格小于,最后把一个区间“夹逼”成一个数,二分法先写两个分支,再根据分支的情况,调整如何取中点。
参考代码 2:

复杂度分析:
时间复杂度: O(NlogN),二分法的时间复杂度为O(logN),在二分法的内部,执行了一次 for 循环,时间复杂度为 O(N),故时间复杂度为O(NlogN)。
空间复杂度:O(1),使用了一个 count 变量,因此空间复杂度为 O(1)。
作者:liweiwei1419
链接:https://leetcode-cn.com/problems/find-the-duplicate-number/solution/er-fen-fa-si-lu-ji-dai-ma-python-by-liweiwei1419/
我的代码:
class Solution {
public:
int findDuplicate(vector<int>& nums)
{
int len = nums.size();
int left = 0;
int right = len - 1;
while(left < right)
{
int mid = (left + right +1) >> 1;
int counter = 0;
for(int num:nums)
{
if(num < mid)
{
counter++;
}
}
if(counter >= mid)
{
right = mid -1;
}
else
{
left = mid;
}
}
return left;
}
};
11.盛最多水的容器
给定 n 个非负整数a1,a2,...,an,每个数代表坐标中的一个点(i, ai)。在坐标内画 n 条垂直线,垂直线i的两个端点分别为(i,ai)和(i,0)。找出其中的两条线,使得它们与x轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且n的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
思路一:
方法一:暴力法
算法
在这种情况下,我们将简单地考虑每对可能出现的线段组合并找出这些情况之下的最大面积。

复杂度分析
时间复杂度:O(n^2),计算所有 {n(n-1)}/{2}种高度组合的面积。
空间复杂度:O(1),使用恒定的额外空间。
方法二:双指针法
算法
这种方法背后的思路在于,两线段之间形成的区域总是会受到其中较短那条长度的限制。此外,两线段距离越远,得到的面积就越大。
我们在由线段长度构成的数组中使用两个指针,一个放在开始,一个置于末尾。 此外,我们会使用变量 maxarea来持续存储到目前为止所获得的最大面积。 在每一步中,我们会找出指针所指向的两条线段形成的区域,更新 maxarea,并将指向较短线段的指针向较长线段那端移动一步。
查看下面的例子将有助于你更好地理解该算法:1 8 6 2 5 4 8 3 7
这种方法如何工作?
最初我们考虑由最外围两条线段构成的区域。现在,为了使面积最大化,我们需要考虑更长的两条线段之间的区域。如果我们试图将指向较长线段的指针向内侧移动,矩形区域的面积将受限于较短的线段而不会获得任何增加。但是,在同样的条件下,移动指向较短线段的指针尽管造成了矩形宽度的减小,但却可能会有助于面积的增大。因为移动较短线段的指针会得到一条相对较长的线段,这可以克服由宽度减小而引起的面积减小。

复杂度分析
• 时间复杂度:O(n),一次扫描。
• 空间复杂度:O(1),使用恒定的空间。
作者:LeetCode
链接:https://leetcode-cn.com/problems/container-with-most-water/solution/sheng-zui-duo-shui-de-rong-qi-by-leetcode/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution {
public:
int maxArea(vector<int>& height)
{
int left = 0;
int right = height.size()-1;
int result = 0;
int tmplong = 0;
int tmpheight = 0;
int tempresult = 0;
while(left <= right)
{
tmplong = right - left ;
if(height[left] <= height[right])
{
tmpheight = height[left];
left++;
}
else
{
tmpheight = height[right];
right--;
}
tempresult = tmplong * tmpheight;
if (tempresult >= result)
{
result = tempresult;
}
}
return result;
}
};
62.不同路径
一个机器人位于一个mxn网格的左上角(起始点在下图中标记为“Start”)。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
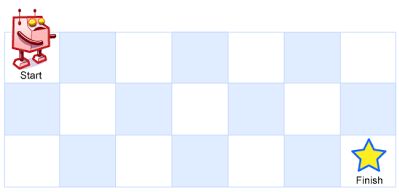
例如,上图是一个7 x 3的网格。有多少可能的路径?
说明:m和n的值均不超过 100。
示例1:
输入: m = 3, n = 2
输出: 3
解释:从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向右 -> 向下
- 向右 -> 向下 -> 向右
- 向下 -> 向右 -> 向右
示例2:
输入: m = 7, n = 3
输出: 28
思路一:排列组合
因为机器到底右下角,向下几步,向右几步都是固定的,
比如,m=3, n=2,我们只要向下 1 步,向右 2 步就一定能到达终点。
所以有 C_(m+n-2)^m

思路二:动态规划
我们令 dp[i][j]是到达i,j最多路径
动态方程:dp[i][j]= dp[i-1][j]+dp[i][j-1]
注意,对于第一行 dp[0][j],或者第一列 dp[i][0],由于都是在边界,所以只能为 1
时间复杂度:O(m*n)O(m∗n)
空间复杂度:O(m * n)O(m∗n)
优化:因为我们每次只需要 dp[i-1][j],dp[i][j-1]
所以我们只要记录这两个数,直接看代码吧!
代码:

优化1:空间复杂度 O(2n)

优化2:空间复杂度 O(n)

作者:powcai
链接:https://leetcode-cn.com/problems/unique-paths/solution/dong-tai-gui-hua-by-powcai-2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
思路二:
从起点(x=0,y=0)出发,下一步只能向右或者向下到达第二点,向右则为 (x+1,y) 向下则为 (x,y+1),一直到 (x=m,y=n)这个点则为结束点视为一条路径。
因此从起点到终点的所有路径总数则为 22 个 以第二个点到终点的路径数的总和。
可以递归求解如下:

但是这种方法会有很多重复计算比如7×3的例子:

而且 7×3的路径总数也可以在计算 m>=7&& n>=3的计算过程中用到。
优化
因为 m,n 都不超过 100,因此可以使用二维数组存下已经计算过的路径数可以避免大量的重复计算。
最终实现结果如下:

作者:rose-chen
链接:https://leetcode-cn.com/problems/unique-paths/solution/cde-di-gui-qiu-jie-by-rose-chen/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
思路三:
这道题目在数据规模较小时可以采用递归求解,且递归的思路较为简单。
对每一个格子赋予一个坐标,初始的格子置为(1,1)。
附上代码

但是数据规模较大时,时间复杂度较大的递归就会tle。此时需要运用动态规划,牺牲空间来换取时间。
定义一个二维数组a[m][n],表示走到这个格子的路径数。由题意容易知道,最上面一行和最左边ll一行可以置为1.
而每一个格子可以由上面的格子往下走一格或左边的格子往右走一格走到。故可以写出下面代码:

作者:Acccccepted
链接:https://leetcode-cn.com/problems/unique-paths/solution/jian-dan-dong-tai-gui-hua-by-acccccepted/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
我的:
class Solution {
public:
int uniquePaths(int m, int n)
{
int b[m][n] = {0};
for(int i = 0; i < m ;i++)
{
b[i][0] = 1;
}
for(int j = 1;j< n;j++)
{
b[0][j] = 1;
}
for(int i = 1;i < m; i++)
{
for(int j = 1;j < n; j++)
{
b[i][j] = b[i][j-1] + b[i-1][j];
}
}
return b[m-1][n-1];
}
};
73. 矩阵置零
给定一个m x n的矩阵,如果一个元素为 0,则将其所在行和列的所有元素都设为 0。请使用原地算法。
示例1:
输入:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
输出:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
示例2:
输入:
[
[0,1,2,0],
[3,4,5,2],
[1,3,1,5]
]
输出:
[
[0,0,0,0],
[0,4,5,0],
[0,3,1,0]
]
进阶:
一个直接的解决方案是使用 O(mn)的额外空间,但这并不是一个好的解决方案。一个简单的改进方案是使用O(m+n)的额外空间,但这仍然不是最好的解决方案。你能想出一个常数空间的解决方案吗?
思路一:
这个问题看上去相当简单,但是需要我们原地更新矩阵,也就是空间复杂度要求是O(1)。我们将用三种不同方法解决这个问题,第一个方法需要额外的存储空间而后两个不用。
方法 1:额外存储空间方法
想法
如果矩阵中任意一个格子有零我们就记录下它的行号和列号,这些行和列的所有格子在下一轮中全部赋为零。
算法
我们扫描一遍原始矩阵,找到所有为零的元素。
如果我们找到 [i, j] 的元素值为零,我们需要记录下行号i和列号j。
用两个sets ,一个记录行信息一个记录列信息。
if cell[i][j] == 0 {
row_set.add(i)
column_set.add(j)
}
最后,我们迭代原始矩阵,对于每个格子检查行 r 和列 c 是否被标记过,如果是就将矩阵格子的值设为 0。
复杂度分析
• 时间复杂度:O(M×N),其中M和N分别对应行数和列数。
• 空间复杂度:O(M+N)。
方法 2:O(1)空间的暴力
想法
在上面的方法中我们利用额外空间去记录需要置零的行号和列号,通过修改原始矩阵可以避免额外空间的消耗。
算法
遍历原始矩阵,如果发现如果某个元素 cell[i][j] 为 0,我们将第 i 行和第 j 列的所有非零元素设成很大的负虚拟值(比如说 -1000000)。注意,正确的虚拟值取值依赖于问题的约束,任何允许值范围外的数字都可以作为虚拟值。
最后,我们遍历整个矩阵将所有等于虚拟值(常量在代码中初始化为 MODIFIED)的元素设为 0。
复杂度分析
时间复杂度: O((M×N)×(M+N)),其中 M和N分别对应行数和列数。尽管这个方法避免了使用额外空间,但是效率很低,因为最坏情况下每个元素都为零我们需要访问所有的行和列,因此所有(M×N) 个格子都需要访问(M+N)个格子并置零。
空间复杂度:O(1)
想法
第二种方法不高效的地方在于我们会重复对同一行或者一列赋零。我们可以推迟对行和列赋零的操作。
作者:LeetCode
链接:https://leetcode-cn.com/problems/set-matrix-zeroes/solution/ju-zhen-zhi-ling-by-leetcode/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
思路二:
**方法1:**赋值另存一个mn的矩阵,在原矩阵为零的值相应置新的矩阵行和列为零。额外空间为O(mn).
方法2:
两个数组,bool[m] 和 bool[n] 分别存某行有零,后者某列有零。之后根据数组值将原矩阵相应位置置零。额外空间O(m + n)。

方法3:(常数额外空间)
- 找到一个零的位置,把这行这列当做方法2中的两个数组存值。
- 根据1的位置的所在行和列的值是否有零将矩阵相应位置置零。
- 再把1中零所在位置的行和列置零。

链接:https://www.cnblogs.com/higerzhang/p/4099114.html
思路三:
这道题的要求是用O(1)的空间,那么我们就不能新建数组,我们考虑就用原数组的第一行第一列来记录各行各列是否有0。
1.先扫描第一行第一列,如果有0,则将各自的flag设置为true
2.然后扫描除去第一行第一列的整个数组,如果有0,则将对应的第一行和第一列的数字赋0再次遍历除去第一行第一列的整个数组,
3.如果对应的第一行和第一列的数字有一个为0,则将当前值赋0最后根据第一行第一列的flag来更新第一行第一列

参考链接:https://www.cnblogs.com/ariel-dreamland/p/9154179.html
我的:
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix)
{
int m = matrix.size();
int n = matrix[0].size();
bool col = false;
bool row = false;
for(int i = 0;i < m ;i++)
{
for(int j = 0;j < n;j++)
{
if(matrix[i][0]==0)
{
row = true;
}
if(matrix[0][j]==0)
{
col = true;
}
}
}
for(int i = 1; i < m;i++)
{
for(int j = 1;j < n;j++)
{
if(matrix[i][j]==0)
{
matrix[i][0]=0;
matrix[0][j]=0;
}
}
}
for(int i = 1; i < m;i++)
{
for(int j = 1;j < n;j++)
{
if(matrix[i][0]==0||matrix[0][j]==0)
{
matrix[i][j]=0;
}
}
}
if(row)
{
for(int i = 0; i < m;i++)
{
matrix[i][0]=0;
}
}
if(col)
{
for(int j = 0; j < n;j++)
{
matrix[0][j]=0;
}
}
}
};
75. 颜色分类
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、1和2分别表示红色、白色和蓝色。
注意:
不能使用代码库中的排序函数来解决这道题。
示例:
输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
进阶:
一个直观的解决方案是使用计数排序的两趟扫描算法。
首先,迭代计算出0、1 和 2 元素的个数,然后按照0、1、2的排序,重写当前数组。
你能想出一个仅使用常数空间的一趟扫描算法吗?
思路一:
方法一: 一次遍历
直觉
本问题被称为 荷兰国旗问题,最初由 Edsger W. Dijkstra提出
其主要思想是给每个数字设定一种颜色,并按照荷兰国旗颜色的顺序进行调整。
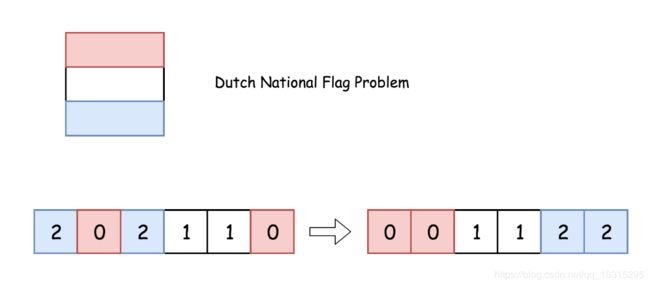
我们用三个指针(p0, p2 和curr)来分别追踪0的最右边界,2的最左边界和当前考虑的元素。

本解法的思路是沿着数组移动 curr 指针,若nums[curr] = 0,则将其与 nums[p0]互换;若 nums[curr] = 2 ,则与 nums[p2]互换。
算法
初始化0的最右边界:p0 = 0。在整个算法执行过程中 nums[idx < p0] = 0.
初始化2的最左边界 :p2 = n - 1。在整个算法执行过程中 nums[idx > p2] = 2.
初始化当前考虑的元素序号 :curr = 0.
While curr <= p2 :
若 nums[curr] = 0 :交换第 curr个 和 第p0个 元素,并将指针都向右移。
若 nums[curr] = 2 :交换第 curr个和第 p2个元素,并将 p2指针左移 。
若 nums[curr] = 1 :将指针curr右移。

复杂度分析
时间复杂度 :由于对长度 N的数组进行了一次遍历,时间复杂度为O(N) 。
空间复杂度 :由于只使用了常数空间,空间复杂度为O(1) 。
作者:LeetCode
链接:https://leetcode-cn.com/problems/sort-colors/solution/yan-se-fen-lei-by-leetcode/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
我的:
若 nums[curr] = 2 :交换第 curr个和第 p2个元素,并将 p2指针左移 。
class Solution {
public:
void sortColors(vector<int>& nums)
{
int current = 0;
int p0 = 0;
int p2 = nums.size() - 1;
while(current <= p2)
{
if(nums[current] == 0)
{
swap(nums[current++],nums[p0++]);
}
else if(nums[current] == 2)
{
swap(nums[current],nums[p2--]);
}
else
{
current++;
}
}
}
};


