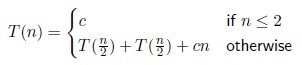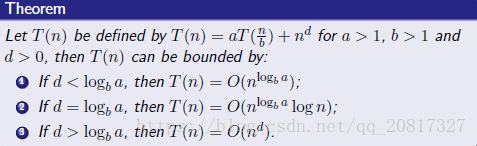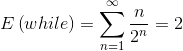计算机算法设计与分析二--分治
1、如果问题和以下数据结构相关，那么把他们分成子问题相对容易
- n维数组
- 矩阵
- n个元素的集合
- 树
- 有向无环图
- 通用图
2、分治算法一般应用于可以分成子问题的问题
实例：
一、排序问题：对一个n维数组排序
输入：一个n维整数数组，A[0..n-1]
输出：递增排序的A插入排序：
时间复杂度：
归并排序：
时间复杂度：
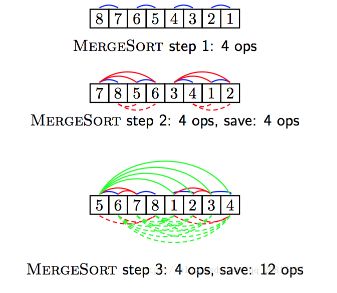
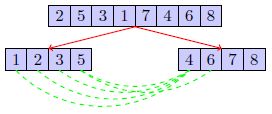
比较两种方法，插入排序和归并排序，从n*n到n*logn节省了哪些环节呢?如下图
虚线的部分即是省略的部分
此外还有个定律：
二、计算n维数组中的逆序对
输入：n个数a1,a2,...an
输出：逆序对个数，如：iaj
暴力破解：
检查每一对(ai,aj)，时间复杂度：O(n*n)，我们有没有更好的方法呢？
直接分治：
时间复杂度：
分治并排序：
就是在归并排序中加了一行，这里n是指||L||+||R||
分治程序包括三个步骤：
- 把问题分成一些子问题，如何分：中间点；通过奇偶分；随机分
- 通过递归来求解子问题
- 将子问题的解合并为原问题的解
快速排序：通过随机的点来划分
但是这种方法最好情况和平均情况下有O(n*logn)，最坏情况下有O(n*n)，我们能否进一步优化呢？
我们可以不找最中心的点（best pivot），我们可以找接近中心的点(good pivots)
选择接近中心的点是容易的：
P(选择中心点)=1/n
P(选择接近中心的点)=1/2
代码：
计算可得
即只需要约两次就可以找到good pivots
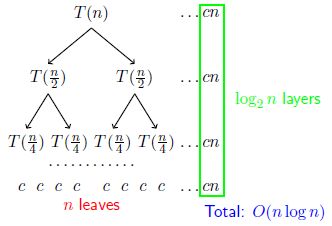
计算时间复杂度：
树的深度为
，每一层合并操作为
所以
三、在数组中选择第k小的数
输入：一个数组A=[A0,A1,...,An-1]
输出：第k小的数或者A的中位数考虑直接排序然后取出第k小的数，时间复杂度为O(n*logn)，我们能不能改进这个算法呢？
考虑分治
计算复杂度：
最坏：每次选择的都是最小的或者是最大的元素
最好：每次都选择最中心的元素
好：每次选择接近中心的元素，如：
和
，
，比如设
，在这种情况下，子问题的规模也呈指数级下降。
所以，选择好的pivot很重要，那么如何选择接近中心的pivots呢？
下面介绍三种算法，分别从不同的角度：
- 通过从中位数中选择pivot：BFPRT算法
- 通过随机选择一个元素来选择pivot：QuickSelect算法
- 通过随机采样选择pivots：FLOYD-RIVEST算法
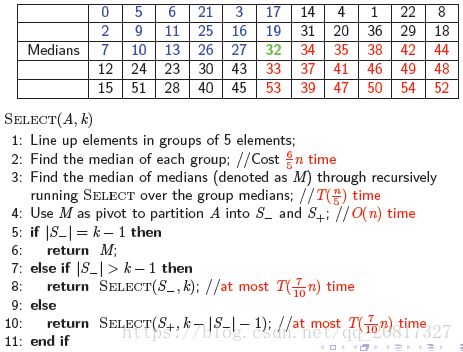
BFPRT算法：在分组的中位数中取中位数
解释：
1、分组，一组5个元素
2、找出每个组的中位元素，有5/n个组，每组最多6步找出中位数（排序），时间复杂度为6n/5
3、通过递归找medians中的中位数（M）
4、通过M把A分成S-和S+，时间复杂度为O(n)
8、有n/5个组，所以有n/10个组在32左边，对于每个组有至少3个小于32，那么有
所以有，
和
10、有n/5个组，所以有n/10个组在32右边，对于每个组有至少3个大于32，那么有
所以有，
和
总时间复杂度计算：
具体代码：
后续我会补上
QuickSelect算法：随机选择一个元素作为pivot
代码：
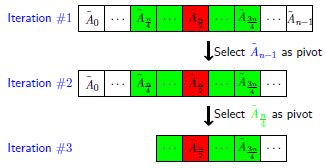
一个例子：
- 选择一个接近中心的pivot将会导致很大的规模下降（上面的例子是降为原先的3/4）
- 选择一个接近中心的pivot大约需要两次迭代（上面已经证明期望为2）
可以证明这个算法的复杂度为O(n)
证明：
- 把问题按规模分期，如
![\left [ n\left ( \frac{3}{4} \right )^{j+1} +1,n\left (\frac{3}{4} \right )^{j}\right ]](http://img.e-com-net.com/image/info8/b3ba73c3a20947cba18e87c86b55295b.gif)
，即![\left [ \frac{3}{4} n+1 ,n\right ]](http://img.e-com-net.com/image/info8/3ee29d6ce43643ab9fbfb69b13c58992.gif)
为0期，![\left [ \frac{9}{16} n+1,\frac{3}{4}n \right ]](http://img.e-com-net.com/image/info8/75f968a2263548fb932347f62f336470.gif)
为1期 - X来表示算法用了多少次的比较，每一期j的比较次数为Xj，X=X0+X1+...，我们想求它的期望
- 对于任意的j期，要找到绿色区域作为pivot的概率为1/2，一旦选择这种pivot，那么规模就变成原来的3/4，并且进入下一期，每一期里期望的迭代次数是2。
- 第j期里最多有多少次比较呢？首先看第0期最多有cn次比较，那么第j期就最多有
次比较，因此，![E\left [ Xj \right ]\leq 2cn\left ( \frac{3}{4} \right )^{j}](http://img.e-com-net.com/image/info8/69b261229cd0477d93b26f701efcc185.gif)
- 因此，
![E\left [ X \right ]=E[X0+X1+...]\leq \sum_{j}2cn\left ( \frac{3}{4} \right )^{j}\leq 8cn](http://img.e-com-net.com/image/info8/21d95c2e36e8401ebfd9cd8fbf5f7564.gif)
FLOYD-RIVEST算法，选择一个pivot基于一个随机的采样
样本是总体的无偏估计
算法：
1、随机有放回的采样，选择r个元素， 把样本设为S。
2、控制S比较小，让u为
处的S的元素，v为
处的S的元素。
3、把A分成三个部分，L，M，H。L比u小，H比v大，M在中间。
4、检测M是否符合条件，可确保M中有中位数。
5、找到中位数
这里我们要精心设计
和
，使M足够大到把中位数包含进去，又要使M足够小，时间复杂度够低（因为最后要对M排序）。
我们可以设
和
，所以M有
大小
所以时间复杂度分析：
总时间复杂度为：
，已经非常的高效。
四、给定平面上的一组点，选择最近的一组点
输入：平面上的n组点
输出：距离最小的一组点1、把平面通过x分为2个大致相等的子集
2、在每一半中找到最接近的点对
3、再考虑一个在左边一个在右边的最近的点对
需要时间复杂度为O(n*n)，能否再改进它呢？
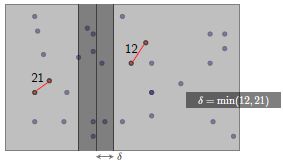
其实，第三步只出现在一个窄的条带中
因此，我们把这个窄条带分成一个个网格，大小为
，为两边最小距离中小的那个。
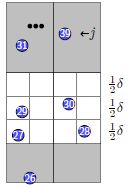
这样对于任何一个点，最多只用选择11个点和它算距离。
最坏情况下，每个网格中都有一个点
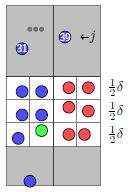
那么对于绿色的点，只需要算右边6个红色的点。
我们可以把所有点按照y排序，其实我们只用计算与绿色点相邻的11个点，因为红色的6个点一定是包含在这11个点里。
代码及其时间复杂度：
这个时间复杂度，我们还可以再改进，这里我们需要引入结构
在第7步中，我们在递归中把两部分排好序。在第8步中，两部分就像MergeSort那样合并，只用花费O(n)的时间，这样时间复杂度就变为