深度学习笔记（0）——机器学习基本概念

本篇博客仅针对毫无机器学习理论背景的人，其他人可以直接跳过。机器学习(machine learning)是最近非常火的一个领域，关于其一些基本定义百度百科、维基百科或者网上随便都可以找到很多资料，所以这里不做过多解释。

就我个人理解，通常任何问题我们都可以用一个数学模型来解释：

y=f(x)

在统计学习方法里面通常使用的是 P(y|x) ，为了方便理解，不妨不严谨地把P看作是一种特殊的 f()

我们解决一个问题有两种模式：一种叫做模型驱动(model driven)，通过研究对象的物理、化学等机理模型，对对象进行建模，从而解决问题，比如我们熟知的牛顿三定律，对于上面那个公式就是我们已知输入 x 和机理模型 f() ，需要求解我们想要得到的 y ；而另外一种叫做数据驱动(data driven)，随着人们遇到的问题越来越复杂，寻找对象机理模型的代价越来越大，反之数据获取的代价越来越小，于是科研工作者开始从另外角度思考问题，是否可以通过这些数据来分析得到我想要的东西，即我知道一些的样本 (x,y) 或者我只知道 x ，我想分析这些来得到对象的模型 f() ，进而当我再次拥有一个 x 的时候，我就可以得到我想要的 y ，如果不是那么严格的来讲，所有这种数据分析的方法都可以算作机器学习的范畴。

所以一个机器学习通常应该包括的基本要素有：训练数据，带参数的模型，损失函数，训练算法。训练数据作用自不必说；带参数的模型是用来逼近 f() ；损失函数是衡量模型优劣的一个指标，比如模型识别分类的准确度；训练算法也可以叫做优化函数，用于不断更新模型的参数来最小化损失函数，得到一个较好的模型，或者叫做学习机。接下来将介绍一些机器学习中的基本概念，可能没有很强的连贯性。

样本数据

样本数据就是我们上文提到的 (x,y) ，其中 x 叫做输入数据(input data)， y 叫做输出数据(output data)或者叫做一个更加专业的名字——标签(label)。通常 x 和 y 都是高维矩阵，以 x 为例：

x=(x1,x2,x3,...,xi)

其中 xi 表示第i个输入样本，比如第i个文字，第i张图片， xi 可以是一维文字向量，二维图片矩阵，三维视频矩阵，或者更加高维的数据类型，以一维向量为例：

xi=(x1i,x2i,x3i,...,xni)

其中 xni 表示 xi 数据的第n个元素的值，比如把图像展平之后第n个像素的灰度值等等。
标签 y 根据需求不同有各种形式，以最简单的n分类问题为例， yi 就是一个n维的one-hot，其中一个值为1，其余的元素都为0，第几个元素为1就表明属于第几个类别。

数据集

完整的数据集表示为 T={(x1,y1),(x2,y2),(x2,y2),...,(xi,yi)} ，对于一个学习机而言，不是所有的数据都用于训练学习模型，而是会被分为三个部分：训练数据、交叉验证数据、测试数据。

• 训练数据(training data)：顾名思义，训练数据用于训练学习模型，通常比例不低于总数据量的一半。
• 交叉验证数据(cross validation data)：交叉验证数据用于衡量训练过程中模型的好坏，因为机器学习算法大部分都不是通过解析法得到的，而是通过不断迭代来慢慢优化模型，所以交叉验证数据就可以用来监视模型训练时候的性能变化。
• 测试数据(testing data)：在模型训练好了之后，测试数据用于衡量最终模型的性能好坏，这也是模型性能好坏的衡量指标，交叉验证的指标只能用于监视和辅助模型训练，不能用来代表模型好坏，所以哪怕交叉验证的准确度是100%而测试数据的准确度是10%，那么模型也是不能被认可的。通常交叉验证和测试数据的比例各占一小半。

特征

特征是机器学习和模式识别领域一个比较特有的名词，在传统机器学习算法中，由于计算性能和参数的限制，所以输入的数据维数不能太高。我们手机随随便便一张照片就有几个MB的数据量，可能会有几百万个像素，这么高维的数据量我们是不能直接输入给学习机的，因此我们需要针对特别的应用提取相对应的特征向量，特征向量的作用主要有两个：

1. 降低数据维度：通过提取特征向量，把原始数据的维度大大较低，简化模型的参数数量。
2. 提升模型性能：一个好的特征，可以提前把原始数据最关键的部分提取出来，因此可以提高学习机的性能。

在传统的机器学习领域，如何提取一个好的特征是大家最关心的，所以机器学习的研究很大程度变成了寻找好的特征，因此也诞生了一个学科叫做特征工程。以下是一个用hog特征进行行人检测的例子，hog特征主要是检测物体的轮廓信息，所以可以用于行人检测。

模型

这里的模型可能用词不准确，但我想表达的是指：带有一些待训练参数，用于逼近前文提到的 f() 的参数集合。在参数空间， f() 只是一个点，而我提到的模型也是一个点，并且由于参数可以变，所以我要做的只是让我模型的这个点尽可能的接近真实 f() 的那个点。机器学习的模型算法有很多，但是比较常用的模型可以概括为三种：

1. 基于网络的模型：最典型的就是神经网络，模型有若干层，每一层都有若干个节点，每两个节点之间都有一个可以改变的参数，通过大量非线性的神经元，神经网络就可以逼近任何函数。
2. 基于核方法的模型：典型的是SVM和gaussian process，SVM把输入向量通过一个核映射到高维空间，然后找到几个超平面把数据分成若干个类别，SVM的核是可以调整。
3. 基于统计学习的模型：最简单的例子就是贝叶斯学习机，统计学习方法是利用数理统计的数学工具来实现学习机的训练，通常模型中的参数是一些均值方差等统计特征，最终使得预测正确概率的期望达到最大。

一个好的学习机模型应该拥有出色的表达逼近能力、易编程实现、参数易训练等特性。

监督与非监督学习

按照任务的不同，学习机可以分为监督学习(supervised learning)和非监督学习(unsupervised)两种，从数学角度来看两者的区别在于前者知道数据的标签 y 而后者不知道样本的标签 y ，所以非监督学习的难度要大一点。

举个通俗的例子，一个母亲交孩子认识数字，当母亲拿到一个数字卡片，告诉孩子这个是数字4是数字6，然后经过大量的教导之后，当目前拿到一个卡片问孩子这个是数字几，这个就是监督学习。如果母亲那一堆数字卡片，让孩子把卡片按照不同数字进行分堆，母亲告诉孩子他分的好不好，可能经过大量的训练，孩子就知道如何把卡片进行正确分堆了，这个就是无监督学习的例子。用一个不那么贴切的名词解释就是，监督学习可以看做分类问题，而无监督可以看做是聚类的问题。

当然还有两种特殊的类型，叫做半监督学习和强化学习，半监督学习是指部分样本是知道标签的，但是其他的样本是不知道标签。强化学习是另外一个特例，为了不混淆大家理解，这里不做解释，感兴趣的可以自行查阅，之后我会单独通过一篇博客来介绍。

监督学习是简单高效的，但是非监督学习是更加有用的，因为人工标注样本标签的代价是非常昂贵耗时的。

损失函数

损失函数(loss function)更严谨地讲应该叫做目标函数，因为在统计学习中有一种目标函数是最大化预测正确的期望概率，我们这里只考虑常见的损失函数。

损失函数是用来近似衡量模型好坏的一个很重要的指标，损失函数的值越大说明模型预测误差越大，所以我们要做的就是不断更新模型的参数，使得损失函数的值最小。常用的损失函数有很多，最简单的如0-1损失函数：

L(y,f(x))={01y=f(x)y≠f(x)

这个损失函数很好理解，预测对了损失为0，预测错了就为1，所以最完美的学习机的损失函数值就应该是0。当然最小二乘误差、交叉熵误差等损失函数也是很常用的，训练时用的损失函数是所有训练样本数据的损失值的和。有了损失函数，模型的训练就变成了一个很典型的优化问题。

优化函数

我们又了目标函数，也就是损失函数，现在我需要一个东西根据损失值来不断更新模型参数，这个东西就叫做优化函数。优化函数的作用就是在参数空间找到损失函数的最优解。梯度下降法是最熟知的优化函数，大家都用下山来形象描述这个算法。假如我们在山上，我们的目标是找到这座山的最低处（最小化损失函数），一个很简单的思路就是我找到当前位置下山角度最大的方向，然后朝着这个方向走，如下图所示

当然这种方法有个问题就是会陷入局部最优点（局部凹坑）出不来，所以各种更加好的优化函数逐渐被大家发现。一个好的优化函数应该有两个性能指标：拥有跳出局部最优解找到全局最优解的能力；拥有更快的收敛速度。

泛化能力、欠拟合和过拟合

泛化能力(generalization ability)是指机器学习模型对未知数据的预测能力，是学习方法本质上重要的性质，现实中采用最多的办法是通过误差来评价学习方法的泛化能力。但是这种评价是依赖测试数据集的，因为测试数据集是有限的，所以这种思路也不能说是完全靠谱，因此有人专门研究泛化误差来更好的表达泛化能力。

欠拟合(underfitting)和过拟合(overfitting)是两种要尽可能避免的模型训练现象，出现这两种现象就说明模型没有达到一个比较理想的泛化能力。欠拟合是指模型复杂度太低，使得模型能表达的泛化能力不够，对测试样本和训练样本都没有很好的预测性能。过拟合则相反，是模型复杂度太高，使得模型对训练样本有很好的预测性能，但是对测试样本的预测性能很差，最终泛化能力也不行。如下图所示，1和4展示的欠拟合，3和6展示的过拟合现象。而一个好的模型应该是如2和5一样，复杂度正合适，泛化能力较强。

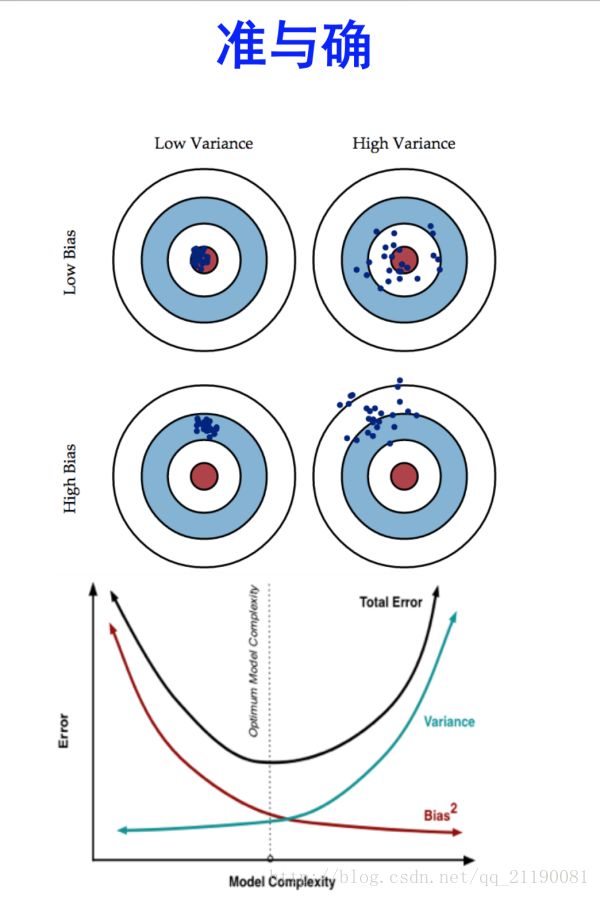
偏差，误差和方差

Bias(偏差)，Error(误差)，和Variance(方差)三者是容易混淆的概念，首先

Error2=Bias2+Variance

Error反映的是整个模型的准确度，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。如下图所示，随着模型的复杂度增加，模型预测的偏差会越来越小，但是方差越来越大，预测结果的分布会散开来。

机器学习和深度学习

目前所说的深度学习通常是指基于神经网络改进的深度学习网络，相比于传统的神经网络，深度学习网络拥有更加高的模型复杂度，所以可以直接把原始数据输入到学习机，不需要人工提取特征。所以如果不从数理角度考虑，传统机器学习和深度学习的最本质区别在于，深度学习拥有训练高复杂度模型能力，所以可以不用人工提取特征，即

深度学习=人工提取特征+传统机器学习方法

推荐书籍

TOM M.MITCHELL. 机器学习(计算机科学丛书)[M]. 机械工业出版社, 2014.

李航. 统计学习方法[M]. 清华大学出版社, 2012.

张学工. 模式识别(第三版)[M]. 清华大学出版社, 2010.