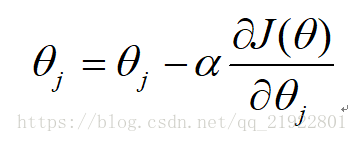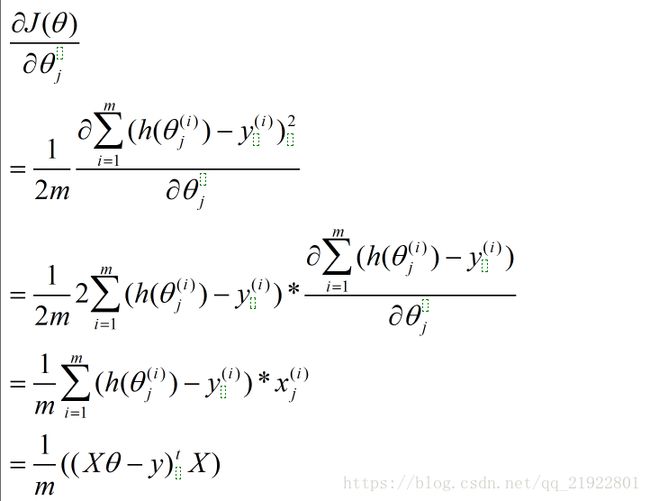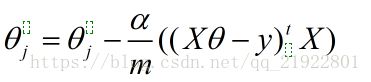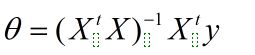机器学习(一)——线性回归的梯度下降算法和正规方程法

机器学习(一)——线性回归的梯度下降算法和正规方程法

---

线性回归

机器学习基本分为有监督学习和无监督学习。

有监督学习基本分为回归问题和分类问题。

回归问题很简单，就是根据样本预测一个连续数的值，类似于模拟信号的预测吧，结果是0.1还是0.2呀，明天降雨量是500mm还是501mm呀。

分类问题自然就是数字信号的预测了，结果是0还是1呀，明天下午还是不下雨呀，这种。

回归问题可以用一条线来拟合样本数据，然后把目标x带入，就得到了目标y。

用一次函数，也就是直线来拟合，就是线性回归了。

---

梯度下降 gradient Descent

一次函数最重要的就是斜率k和截距b，也就是两个参数而已，θ₀，θ₁。
也就是y=θ₀+θ₁*x。

现在任务简单了，确定θ向量，使尽可能多的数据点落在直线上，。

任务进一步变成了，使所有点到直线的距离的和最小，所以需要一个叫做代价函数的东西，J(θ)。它表示所有点到直线的距离和，那么总有一组θ，使得J最小，这个θ就是我们要找的。

但是θ总不可能一步得到，所以需要随便选个θ，然后让计算机帮我们慢慢调整到合适的地方，就好像牛顿迭代法求零点一样，这个过程下面会仔细讲到。

好了，当调整到合适的地方，也就是找到了不错的θ后，我们的直线就画出来了，只需要带入目标x，就可以得到预测值y了，完美。

1、hypothesis，假设函数

在上面的介绍中，其实已经有了hypothesis了，那就是y=θ₀+θ₁*x.

意思很简单，就是去猜猜看数据集满足什么样子的函数，一次的，二次的，根号，然后写个样子出来就好了，参数当然是每个特征有个参数。

哦，先介绍下变量。

X假设是一个m*n的矩阵，m表示有m个样本，n表示有n个特征，一般来说如果是n个特征，应该是有n+1维，因为X₀应该是1，用来对应上面所显示的θ₀，也就是常数项。后面的维度和这个对应就好。
θ是n*1的矩阵，在hypothesis中对应每个特征的参数。
y是m*1的矩阵，显然，它就是数据集中每条样本的结果。

所以，X*θ=y。 那么，hypotgesis也可以表示为 h(θ)=Xθ 。

2、cost function，代价函数

代价函数也介绍过了，就是根据θ计算所有点到当前直线的距离，然后程序会自动调整直线。

距离就是直线的y值减去样本对应x的y值咯，不想取绝对值，就用平方代替了，所以代价函数就变成了:

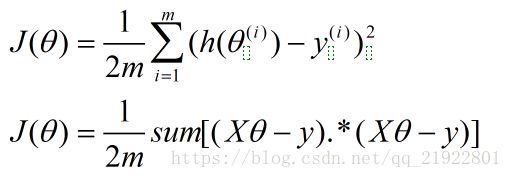
上面一个是普通的形式，下面转换成了矩阵的形式。

每一个预测的y减去样本的y，求平方，再求和，除以样本数量*2，这个2是因为后面求导会方便一点。

3、迭代

好了，最重要的部分来了。

代价函数J(θ)的自变量是θ，应变量是距离和。

代价函数的目标是使距离最小，也就是找到θ使J最小，ok，这简直就是牛顿迭代法的翻版。

牛顿迭代法是给个二次函数，也就是一条曲线，然后随便取个值，然后求这个值的导数，用这个值减去倒数*α，一直循环到y值为0，脑补下这个过程呗，不想画图了。
α大概表示步距吧，所以α不能太大，一步跨过了最小值，就又变大了，，当然α也不能太小，要不然迭代到啥时候去。

所以这里虽然不是求零点，但是也是求最小值，其实是一样的。

所以迭代过程就是:

其中的偏导数需要化简，过程如下:

所以最后，迭代过程就是:

至于什么时候停止，可以通过代码检测，发现导数接近0了，或者导数的导数接近0了，那就差不多了。当然也可以画图肉眼判断喽，把每次J的值画出来，发现最后基本不随着迭代的进行变化了，且一直在减小，那就说明差不多了。

好了，到这里为止，θ已经被找到了，带到hypothesis里面预测我们的目标就搞定了。

4、tips

可以进行特征的缩放，让所有特征范围差不多大，这样可以下降的快一点，一般做法是对某个特征减去这个特征所有样本的平均数再除以标准差。

需要注意的是，最后在进行预测的时候，需要对预测的x做相应变化。

---

正规方程 normal Equations

其实这个才是正常情况下首先应该想到的方法，

之前也写过，X*θ=y

稍微进行下变换，就可以了

左乘X^-1，不就得到θ了吗，可是X不一定是方阵，所以先变成方阵再说，左乘X的转置。

思路就是这样，最后结果是:

这个方法在低纬度的时候好用，因为一次到位，但是维度高了之后可能矩阵就算就有一丢丢麻烦了，利弊我也说不清，刚入门，先学着再说。