GBDT原理与Sklearn源码分析-回归篇

摘要：

本文将非常详细的介绍GBDT（Gradient Boosting Decision Tree）的原理以及Sklearn里面具体是如何实现一个GBDT的。本次内容将分为两篇文章，一篇是GBDT用于回归，一篇是GBDT用于分类任务。虽然两者其实本质是一样的，只是loss function不同，但是分成两篇可以帮助更好的对比理解。

注意：本文前半部分是GBDT原理的一个概述，后半步是sklearn中是如何实现的，以及给出一个具体例子一步步和读者分享整个算法的流程（本文也侧重于这一点）

1.GB原理概述

注意：对原理已经熟知或者不想太多了解者可直接跳过看实践部分，另外在学习GBDT前非常建议读者先看一下李航老师的《统计学习方法》中的8.4.1节。

首先，先解释一下所谓的boosting（提升）。提升方法就是从弱学习算法出发，反复学习，得到一系列的弱分类器（基分类器），然后组合这些弱分类器，构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布（训练数据的权值分布）。

所以，对于提升方法来说，需要解决两个问题：一是每一轮学习中，如何改变训练数据的权值或者概率分布；二是如何将弱分类器组合成一个强分类器。

了解了所谓的boosting后，我们得到上面的两个问题，对于第一个问题，在GBDT中，其实就是通过拟合损失函数的负梯度值在当前模型的值，这里需要注意的，在以前的机器学习算法中，我们都是通过直接拟合真实值，而在GBDT里，我们拟合的目标不再是真实值，而是一个梯度值，当然这个梯度值和真实值有关系，后面部分会说明。

对于第二个问题，GBDT中的基分类器当然是决策树。但是决策树有很多比如C4.5、ID3、CART等等。那么用的是哪种树？在GBDT里，用的是CART（分类与回归树），同时Sklearn里面实现GBDT时用的基分类器也是CART。

---

为了前后连贯，这里简单介绍一下CART。一般的CART是这样的：用于分类任务时，树的分裂准则采用基尼指数，用于回归任务时，用MSE（均方误差）。
注意：当然在回归任务中，分裂准则也不再局限于用MSE，也可以用MAE，还可以用Friedman_mse（改进型的mse)。

---

上面提到，CART可以用于回归和分类，那么到底用回归还是分类呢？上面我们已经提到了，GBDT拟合的目标是一个梯度值，这个值当然是一个连续值或者说实值，所以在GBDT里，通通都是回归树。

有了基分类器后，如何将这些基分类器组合起来？boosting方法一般是使用加法模型。
即： fM(x)=∑Mm=1T(x,θm) f M ( x ) = ∑ m = 1 M T ( x , θ m )

其实利用GB训练强学习器的思路，总结下来就是下面这个过程：

---

对于算法的第3步： yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x) y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) ,就是我们上面说的损失函数的负梯度在当前模型的值。
也就是说，我们每一个颗回归树拟合的目标是 yi~ y i ~ 。

这里这样说可能比较抽象，我们举几个例子：
比如说，损失函数选择使用：
L(yi,F(xi))=(12)∗(yi−F(xi))2 L ( y i , F ( x i ) ) = ( 1 2 ) ∗ ( y i − F ( x i ) ) 2 ,那么其负梯度值为： −[∂L(yi,F(xi))∂F(xi)]=(yi−F(xi)) − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] = ( y i − F ( x i ) ) ，再带入当前模型的值 F(x)=Fm−1(x) F ( x ) = F m − 1 ( x ) 。
则有：
yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=(yi−Fm−1(xi)) y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = ( y i − F m − 1 ( x i ) )
所以我们能看到，当损失函数选用Least-square时，每一次拟合的值就是（真实值-当前模型的值）。

比如说，损失函数选择Least-absolute使用：
L(yi,F(xi))=∣∣yi−F(xi)∣∣ L ( y i , F ( x i ) ) = | y i − F ( x i ) | ，其梯度值为：
yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=sign(yi−Fm−1(xi)) y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = s i g n ( y i − F m − 1 ( x i ) )
其中 sign s i g n 是符号函数。

比如说，损失函数选择使用logistic loss时：(二分类任务）
L(yi,F(xi))=yilog(pi)+(1−yi)log(1−pi) L ( y i , F ( x i ) ) = y i l o g ( p i ) + ( 1 − y i ) l o g ( 1 − p i ) 。
其中 pi=11+e−F(xi) p i = 1 1 + e − F ( x i ) 。
其梯度值为：
yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=yi−11+e−Fm−1(xi) y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = y i − 1 1 + e − F m − 1 ( x i ) （这个简单推导过程在下一篇文章有，以及多分类任务采用的loss-function)

---

对于算法的第4步，在这里先简单提一下，其目的就是为了求一个最优的基分类器。对于不同的基分类器有不同的寻找，比如，对于决策树，寻找一个最优的树的过程其实依靠的就是启发式的分裂准则。

---

对于算法的第5步，是一个Line search 的过程，具体可以参考Friedman的文章。在GBDT里，通常将这个过程作为Shrinkage，也就是把 ρm做为学习率 ρ m 做 为 学 习 率 ，后面实践部分可以看到效果。

---

对于算法的第6步，求得新的基分类器后，利用加法模型，更新出下一个模型 Fm(x) F m ( x )

---

大家可以发现，对于算法的第1步我没有提到，这是因为，这个需要在讲完第3步才能够说明。算法的第1步是一个初始化的过程。为什么需要初始化？很简单，因为每次在计算负梯度值时需要用到前一个模型 Fm−1(xi) F m − 1 ( x i ) 预测的值。对于我们训练的第一个模型 m=1 m = 1 而言需要有 F0(xi) F 0 ( x i ) 的存在。

那么 F0(x) F 0 ( x ) 初始化为多少？这个取决于loss function的选择，下面给出一般的做法：
当loss function选择MSE时， F0(x)=y¯ F 0 ( x ) = y ¯ ， y¯ y ¯ 为样本真实值的平均值。比如有数据集：

那么 F0(x)=y¯=7.306 F 0 ( x ) = y ¯ = 7.306

当loss function选择MAE时， F0(x)=mediany F 0 ( x ) = m e d i a n y ，也就说用真实值的中位数作为初始值。

当loss function选择logisit loss时， F0(x)=(12)∗log(∑yi∑(1−yi)) F 0 ( x ) = ( 1 2 ) ∗ l o g ( ∑ y i ∑ ( 1 − y i ) )
这里需要注意的是，这里就是利用对数几率来初始化，分子 ∑yi ∑ y i 就是正样本的个数，分母就是负样本的个数。
比如说，对于数据集：

F0(x)=(12)∗log(∑yi∑(1−yi))=(12)∗log(37) F 0 ( x ) = ( 1 2 ) ∗ l o g ( ∑ y i ∑ ( 1 − y i ) ) = ( 1 2 ) ∗ l o g ( 3 7 )

另外，再介绍一个Loss function，指数损失。具体表达为：
L(yi,F(xi))=e−yF(xi) L ( y i , F ( x i ) ) = e − y F ( x i ) ，其负梯度大家可以自己求求，后面有汇总表给大家参考。

其初始化和上面提到Logisit loss的初始化是一样的。

2.GBDT原理-2

上面我们初步介绍一下GB以及其整个流程，但是我们前面介绍的只是GB的思想，也就是说，对于任意的基分类器都可以利用GB的思想训练一个强分类器。而把基分类器选为决策树（DT)时，就是我们常用的GBDT。
那么对于GBDT来说，其训练过程是怎么样的？对于回归任务。
当我们选择的loss function为Least-square。
即 L(yi,F(xi))=(12)∗(yi−F(xi))2 L ( y i , F ( x i ) ) = ( 1 2 ) ∗ ( y i − F ( x i ) ) 2
其伪代码(简化版)：

Algorithm 2:LS_TreeBoost____________________________________F0(x)=y¯Form=1 to M do:       yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=(yi−Fm−1(xi))       {Rjm}J1=J−terminal node tree({ỹ i,xi}N1)       γjm=avexi∈Rjmyi~       Fm(x)=Fm−1(x)+∑j=1JγjmI(x∈Rjm) A l g o r i t h m   2 : L S _ T r e e B o o s t _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ F 0 ( x ) = y ¯ F o r m = 1   t o   M   d o :               y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = ( y i − F m − 1 ( x i ) )               { R j m } 1 J = J − t e r m i n a l   n o d e   t r e e ( { y ~ i , x i } 1 N )               γ j m = a v e x i ∈ R j m y i ~               F m ( x ) = F m − 1 ( x ) + ∑ j = 1 J γ j m I ( x ∈ R j m )

上面的伪代码中的基本步骤和Algorithm 1的一样。下面分析一下步骤4和步骤5。

对于步骤4：
其想表达的是以 {ỹ i,xi}N1 { y ~ i , x i } 1 N 为训练数据，拟合一颗回归树，最终得到叶子节点的区域。（详细的见下）

对于步骤5：
在步骤4我们得到叶子节点对应的区域，那么叶子节点的取值为多少？也就是这颗树到底输出多少？
在Friedman的论文中有这部分的推导。这里简单总结一下：
叶子节点的取值和所选择的loss function有关。对于不同的Loss function，叶子节点的值也不一样。

首先，记第 m m 颗树的第 j j 个叶子节点的值为 γjm γ j m
比如，选择MSE作为loss function时：
γjm=avexi∈Rjmyi~ γ j m = a v e x i ∈ R j m y i ~ ， yi~ y i ~ 为梯度值。
比如，选择MAE作为Loss function时：
γjm=medianxi∈Rjm(yi−Fm−1(xi)) γ j m = m e d i a n x i ∈ R j m ( y i − F m − 1 ( x i ) )
比如，选择Logistic loss作为Loss function时：
γjm=∑Ni=1yi~∑Ni=1(yi−yi~)∗(1−yi+yi~) γ j m = ∑ i = 1 N y i ~ ∑ i = 1 N ( y i − y i ~ ) ∗ ( 1 − y i + y i ~ )
比如，选择指数损失作为loss function时：
γjm=∑Ni=1(2yi−1)e(−(2yi−1)Fm−1(xi))∑Ni=1e(−(2yi−1)Fm−1(xi)) γ j m = ∑ i = 1 N ( 2 y i − 1 ) e ( − ( 2 y i − 1 ) F m − 1 ( x i ) ) ∑ i = 1 N e ( − ( 2 y i − 1 ) F m − 1 ( x i ) ) 。

这些叶子节点的取值推导过程在论文中其实也只是几笔带过，有兴趣的可以深入研究为何。

最后一个步其实就是把前面已经训练的 m−1 m − 1 颗树预测的结果加上刚训练好的第 m m 颗树的预测结果。

3.GBDT实践以及Sklearn源码分析

相信看完上面后还是感觉对GBDT的训练过程有些模糊，下面就以一个数据集出发，一步一步走GBDT的训练过程，并且同时分析Sklearn里面GBDT的源码。
为了方便说明，我们用下面这个很简单的数据。

xi x i	1	2	3	4	5	6	7	8	9	10
ỹ i y ~ i	5.56	5.7	5.91	6.4	6.8	7.05	8.9	8.7	9.	9.05

1. 选择MSE做为建树的分裂准则
2. 选择MSE作为误差函数
3. 树的深度设置为1

根据算法2，第一步我们需要初始化 F0(x) F 0 ( x ) ，因此 F0(x)=7.307 F 0 ( x ) = 7.307

---

拟合第一颗树（ m=1 m = 1 ）
由公式，可以计算负梯度值：
yi~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=(yi−Fm−1(xi)) y i ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = ( y i − F m − 1 ( x i ) )
具体结果如下表：

xi x i	1	2	3	4	5	6	7	8	9	10
ỹ i y ~ i	-1.747	-1.607	-1.397	-0.907	-0.507	-0.257	1.593	1.393	1.693	1.743

得到梯度值后，下面就是以 ỹ i y ~ i 为目标值进行拟合。

---

这里简单介绍一下决策树建树的过程：
决策树学习最关键的步骤就是选择最优划分属性，一般而言，随着划分不过程不断的进行，我们希望决策树的分支节点所包含的样本尽可能属于同一类别（方差小）。通常，我们会选择一个准则来评价划分的质量，比如回归树中经常使用的MSE（这种方法属于启发式的）
对于连续值，我们可以穷尽每个值 v v ，把每个值 v v 作为一个分裂点( <=v <= v 和 >v > v ),然后计算两个分支的 MSEleft、MSEright M S E l e f t 、 M S E r i g h t 。
选择最小的 MSEsum=MSEleft+MSEright M S E s u m = M S E l e f t + M S E r i g h t 的分裂点 v v
对于类别型特征，我们有类似的做法，通过 = = 和 ≠ ≠ 来划分。

---

当选择 1 1 作为分裂点时候， MSEleft=0 M S E l e f t = 0 , MSEright=1.747 M S E r i g h t = 1.747
当选择 2 2 作为分裂点时候， MSEleft=0.0049 M S E l e f t = 0.0049 , MSEright=1.5091 M S E r i g h t = 1.5091
依次，穷尽所有取值。
可以得到当选择 6 6 作为分裂点时 MSEsum=0.3276 M S E s u m = 0.3276 最小。

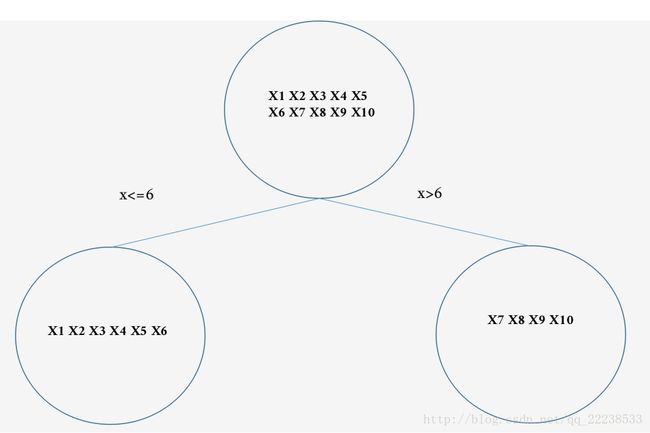
至此，我们完成了第一颗树的拟合，拟合完之后我们得到了 Rjm R j m 以及 、γjm 、 γ j m
具体为：
R11为xi<=6 R 11 为 x i <= 6 ， R21为xi>6 R 21 为 x i > 6 、
γ11=(ỹ 1+ỹ 2+ỹ 3+ỹ 4+ỹ 5+ỹ 6)6=−1.0703 γ 11 = ( y ~ 1 + y ~ 2 + y ~ 3 + y ~ 4 + y ~ 5 + y ~ 6 ) 6 = − 1.0703
γ21=(ỹ 7+ỹ 8+ỹ 9+ỹ 10)4=1.6055 γ 21 = ( y ~ 7 + y ~ 8 + y ~ 9 + y ~ 10 ) 4 = 1.6055

最后更新 F1(xi) F 1 ( x i ) 值， F1(xi)=F0(xi)+∑2j=1γj1I(xi∈Rj1) F 1 ( x i ) = F 0 ( x i ) + ∑ j = 1 2 γ j 1 I ( x i ∈ R j 1 ) 。
比如更新其中一个样本 x1 x 1 的值：
F1(x1)=F0(x1)+∑2j=1γj1I(x1∈Rj1)=7.307−1.0703=6.2367 F 1 ( x 1 ) = F 0 ( x 1 ) + ∑ j = 1 2 γ j 1 I ( x 1 ∈ R j 1 ) = 7.307 − 1.0703 = 6.2367 。

这里需要注意的是，前面我们提到一个算法步骤是Line search（具体见论文）。在GBDT里，我们通过不会直接把上一个轮的预测值 Fm−1(x) F m − 1 ( x ) 直接加上 ∑Jj=1γjmI(xi∈Rjm) ∑ j = 1 J γ j m I ( x i ∈ R j m ) ，而是会在 ∑Jj=1γjmI(xi∈Rjm) ∑ j = 1 J γ j m I ( x i ∈ R j m ) 乘上一个学习率。可以理解，因为如果每次完全加上（学习率为1）本轮模型的预测值容易导致过拟合。所以通常在GBDT中的做法（也叫Shrinkage)是：
Fm(x)=Fm−1(x)+η∗∑Jj=1γjmI(x∈Rjm) F m ( x ) = F m − 1 ( x ) + η ∗ ∑ j = 1 J γ j m I ( x ∈ R j m ) 。 η η 为学习率。所以，当 η=0.1 η = 0.1 时，上面的计算结果变为：
F1(x1)=F0(x1)+0.1∗∑2j=1γj1I(x1∈Rj1)=7.307−0.1∗1.0703=7.1997 F 1 ( x 1 ) = F 0 ( x 1 ) + 0.1 ∗ ∑ j = 1 2 γ j 1 I ( x 1 ∈ R j 1 ) = 7.307 − 0.1 ∗ 1.0703 = 7.1997 。

至此一轮迭代（第一个颗树拟合）完成，下面开始第二轮迭代（第二颗树拟合）。

---

拟合第二颗树（ m=2 m = 2 )
比如，这里示范计算 ỹ 1 y ~ 1 。
y1~=−[∂L(yi,F(xi))∂F(xi)]F(x)=Fm−1(x)=(y1−F1(x1))=(5.56−7.19996)=−1.63996667 y 1 ~ = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = ( y 1 − F 1 ( x 1 ) ) = ( 5.56 − 7.19996 ) = − 1.63996667
其他由公式计算可以得到下表：

xi x i	1	2	3	4	5	6	7	8	9	10
ỹ i y ~ i	-1.63996667	-1.49996667	-1.28996667	-0.79996667	-0.39996667	-0.14996667	1.43245	1.23245	1.53245	1.58245

因此，在第二颗树中，拟合的是新的梯度值。下面的过程就是建树->计算叶子节点的值、叶子节点的区间->更新 F2(x) F 2 ( x ) 。所以就不在累述了。
最后得到两个叶子节点值分别为：
γ12=−0.9633 γ 12 = − 0.9633
γ22=1.44495 γ 22 = 1.44495

最后，我们来看一下如何进行预测。

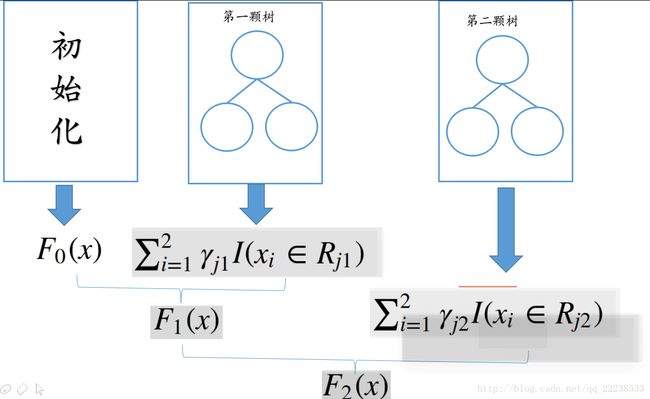
当只有两颗树的时候， F2(x) F 2 ( x ) 即为预测的结果。

总结-1

我们先来简单的总结一下。
回头看，其实GBDT的思路是很简单的，每一次用一个回归树来拟合一个梯度值。而这个梯度值就只是损失函数的一阶导数在当前模型的取值。拟合完一颗树之后，需要计算叶子节点的值，而这个值是和损失函数有关的，当然，数学大神们已经为我们计算好常用的一些损失函数的叶子节点取值。最终预测结果其实就是每一颗树的预测结果相加，所以整个过程都非常的好理解。

Sklearn源码分析

下面这一部分是简单分析一下Sklearn中是如何实现GBDT的。GBDT大部分过程的代码都会涉及，但是源码中有一部分是用cython写的，而这一部分在github上面虽然有.pyx程序，但是还是把关键的部分删掉了，比如说split_node（建树的过程）。
所以没有办法呈现一个完整的分析过程，所以下面挑一些代码分析。

Sklearn里面，当loss function选择mse时，计算负梯度值、计算叶子节点的值是在一个叫LeastSquaresError的类里面实现的。

class LeastSquaresError(RegressionLossFunction):
    """Loss function for least squares (LS) estimation.
    Terminal regions need not to be updated for least squares. """
    def init_estimator(self):
        return MeanEstimator()

    def __call__(self, y, pred, sample_weight=None):
        if sample_weight is None:
            return np.mean((y - pred.ravel()) ** 2.0)
        else:
            return (1.0 / sample_weight.sum() *
                    np.sum(sample_weight * ((y - pred.ravel()) ** 2.0)))

    def negative_gradient(self, y, pred, **kargs):
        return y - pred.ravel()

    def update_terminal_regions(self, tree, X, y, residual, y_pred,
                                sample_weight, sample_mask,
                                learning_rate=1.0, k=0):
        """Least squares does not need to update terminal regions.

        But it has to update the predictions.
        """
        # update predictions
        print ("树节点值",tree.value)
        y_pred[:, k] += learning_rate * tree.predict(X).ravel()
    def _update_terminal_region(self, tree, terminal_regions, leaf, X, y,
                                residual, pred, sample_weight):
        pass

其中，下面这个方法就是计算负梯度值。

    def negative_gradient(self, y, pred, **kargs):
        return y - pred.ravel()

下面这个是用于初始化的：

class MeanEstimator(object):
    """An estimator predicting the mean of the training targets."""
    def fit(self, X, y, sample_weight=None):
        if sample_weight is None:
            self.mean = np.mean(y)
        else:
            self.mean = np.average(y, weights=sample_weight)

    def predict(self, X):
        check_is_fitted(self, 'mean')
        y = np.empty((X.shape[0], 1), dtype=np.float64)
        y.fill(self.mean)
        return y

可以看到，对于mse，初始化的使用均值。

    def fit(self, X, y, sample_weight=None):
        if sample_weight is None:
            self.mean = np.mean(y)
        else:
            self.mean = np.average(y, weights=sample_weight)

下面这个是更新 Fm(x) F m ( x ) 的值：

    def update_terminal_regions(self, tree, X, y, residual, y_pred,
                                sample_weight, sample_mask,
                                learning_rate=1.0, k=0):
        """Least squares does not need to update terminal regions.

        But it has to update the predictions.
        """
        # update predictions
        y_pred[:, k] += learning_rate * tree.predict(X).ravel()

注意到，每次更新的时候会乘上一个learning_rate（学习率）
最后一个核心部分就是建树。

            # induce regression tree on residuals
            tree = DecisionTreeRegressor(
                criterion=self.criterion,
                splitter='best',
                max_depth=self.max_depth,
                min_samples_split=self.min_samples_split,
                min_samples_leaf=self.min_samples_leaf,
                min_weight_fraction_leaf=self.min_weight_fraction_leaf,
                min_impurity_decrease=self.min_impurity_decrease,
                min_impurity_split=self.min_impurity_split,
                max_features=self.max_features,
                max_leaf_nodes=self.max_leaf_nodes,
                random_state=random_state,
                presort=self.presort)

可以看到利用了一个回归树来拟合梯度值。
上面的这些代码已经涵盖了GBDT的基本思路：
初始化->计算负梯度值->用回归树拟合负梯度值->计算叶子节点值->更新 Fm(x) F m ( x ) 。
对于建树部分的代码貌似还没有开放出来（可能是我没找到），如果读者有的话请分享一下。

总结-2

大致介绍了一下GBDT的原理以及实践过程和在sklearn里面GBDT的核心代码。由于篇幅不想太长，所以把其余想分享的东西留到下一篇文章中。希望对大家理解GBDT有所帮助。