强化学习 入门(二)
强化学习 入门(二)
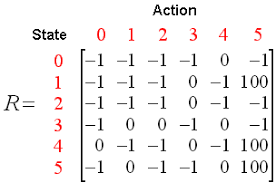
一、Q-learning:Q-table
公式 :
更新规则:相当于以前有个old的值,现在又发现了个new的值,该用哪一个呢?
- 只用新的,相当于彻底放弃已有经验。
- 只用老的,相当于不更新。
- 各取一半,相当于取个平均。
那就老规矩,加个权重,引入了权重 $α $,得到了更新公式。
Q l a t e s t = ( 1 − α ) Q o l d + α Q n e w = Q o l d + α ( Q n e w − Q o l d ) Q_{latest}=(1-α )Q_{old}+α Q_{new} =Q_{old}+α (Q_{new}-Q_{old}) Qlatest=(1−α)Qold+αQnew=Qold+α(Qnew−Qold)
Q [ s , a ] = Q [ s , a ] + α ( r + γ m a x a ′ Q [ s ′ , a ′ ] − Q [ s , a ] ) Q[s,a]=Q[s,a]+α(r+γ\ \underset{a′}{\mathrm{max} }\ Q[s′,a′]−Q[s,a]) Q[s,a]=Q[s,a]+α(r+γ a′max Q[s′,a′]−Q[s,a])
二、Deep Q Network :神经网络对Q-函数进行建模
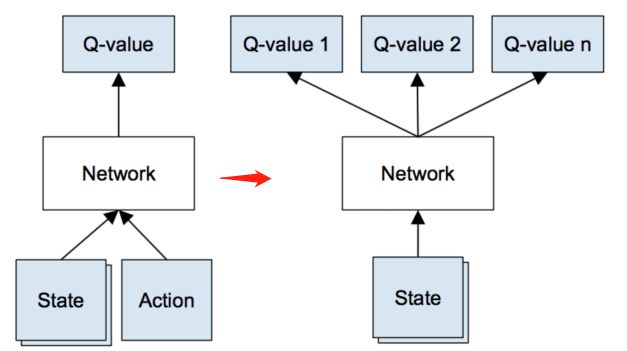
q-table 存在一个问题,真实情况的state可能无穷多,这样q-table就会无限大,解决这个问题的办法是通过神经网络实现 q-table。输入一个 state,输出在该 state 下多个不同 action(一般 action 有限,比如 flappy bird 的像素点 state 很多,但操作的 action 只有上下左右)的 q-value。
用一个函数来表示Q(s,a)。即
Q [ s , a ] = f ( s , a ) Q[s,a] = f(s,a) Q[s,a]=f(s,a)
如线性表达式: Q [ s , a ] = f ( s , a ) = w 1 s + w 2 a + constant ≈ f ( w , s , a ) Q[s,a] = f(s,a)= w_1s+w_2a+\text{constant}≈f(w,s,a) Q[s,a]=f(s,a)=w1s+w2a+constant≈f(w,s,a)
训练最重要的技巧是 经验回放(experience replay)
在玩游戏的过程中, 所有经历的都被记录起来。训练神经网络时, 我们从这些记录的中随机选取一些mini-batch作为训练数据训练, 而不是按照时序地选取一些连续的。按时序选取, 训练实例之间相似性较大, 网络很容易收敛到局部最小值。
Q ( s ) ≈ f ( s , w ) 只输入不同的 s → [ Q ( s , a 1 ) … Q ( s , a n ) ] Q(s)≈f(s,w) \ \ \underrightarrow{\text{只输入不同的 $s$}} \ \ [Q(s,a_1)…Q(s,a_n)] Q(s)≈f(s,w) 只输入不同的 s [Q(s,a1)…Q(s,an)]
三、Q函数怎么神经网络化
1、DL与RL结合的问题
- DL需要大量带标签的样本进行监督学习;RL只有reward返回值,而且伴随着噪声,延迟(过了几十毫秒才返回),稀疏(很多State的reward是0)等问题;
- DL的样本独立;RL前后state状态相关;
- DL目标分布固定;RL的分布一直变化,比如你玩一个游戏,一个关卡和下一个关卡的状态分布是不同的,所以训练好了前一个关卡,下一个关卡又要重新训练;
- 过往的研究表明,使用非线性网络表示值函数时出现不稳定等问题。
2、DQN解决问题方法
- 通过Q-Learning使用reward来构造标签(对应问题1)
- 通过experience replay(经验池)的方法来解决相关性及非静态分布问题(对应问题2、3)
- 使用一个NN(MainNet)产生当前Q值,使用另外一个NN(Target)产生Target Q值(对应问题4)
LOSS function: L ( θ ) = E [ ( T a r g e t Q − Q ( s , a ; θ ) ) 2 ] L(\theta)=E[(TargetQ-Q(s,a;\theta))^2] L(θ)=E[(TargetQ−Q(s,a;θ))2]
T a r g e t Q = r + γ max a ′ Q ( s ′ , a ′ ; θ ) TargetQ = r+\gamma \max_{a'}Q(s',a';\theta) TargetQ=r+γa′maxQ(s′,a′;θ)
3、经验池(experience replay)
经验池的功能主要是解决相关性及非静态分布问题。具体做法是把每个时间步agent与环境交互得到的转移样本 ( s t , a t , r t , s t + 1 ) (s_t, a_t, r_t,s_{t+1}) (st,at,rt,st+1)储存到回放记忆单元,要训练时就随机拿出一些(minibatch)来训练。(其实就是将游戏的过程打成碎片存储,训练时随机抽取就避免了相关性问题)
四、Exploration-Exploitation
假设你家附近有十个餐馆,到目前为止,你在八家餐馆吃过饭,知道这八家餐馆中最好吃的餐馆可以打8分,剩下的餐馆也许会遇到口味可以打10分的,也可能只有2分,如果为了吃到口味最好的餐馆,下一次吃饭你会去哪里?
- 探索:是指做你以前从来没有做过的事情,以期望获得更高的回报
- 利用:是指做你当前知道的能产生最大回报的事情。
那么,你到底该去哪家呢?这就是探索-利用困境。
如果你是以每次的期望得分最高,那可能就是一直吃8分那家餐厅;但是你永远突破不了8分,不知道会不会吃到更好吃的口味。所以只有去探索未知的餐厅,才有可能吃到更好吃的,同时带来的风险就是也有可能吃到不和口味的食物。
Q-learning 算法尝试解决信用分配问题,依旧存在的是探索-利用困境。
在游戏开始阶段, Q-table或Q-network是随机初始化的。 它给出的Q-值最高的动作是完全随机的, 智能体表现出的是随机的“探索”。
当Q-函数收敛时, 随机“探索” 的情况减少。 所以, Q-learning中包含“探索” 的成分。 但是这种探索是“贪心” 的, 它只会探索当前模型认为的最好的策略。
修正: ϵ \epsilon ϵ-贪心探索
以 ϵ \epsilon ϵ 的概率选取随机的动作做为下一步动作, 1 − ϵ 1-\epsilon 1−ϵ 的概率选取分数最高的动作。
五、参考文献:
http://www.hugiss.com/reinforcementlearning-intro/
http://fromwiz.com/share/s/1CGZRH2S1Aro2gtjMB0TJPbh2WMt0I1fPkJq26Z6cI3pS8GI
http://blog.csdn.net/young_gy/article/details/73485518#deep-q-learning
http://blog.csdn.net/xbinworld/article/details/79372777
https://zhuanlan.zhihu.com/p/21421729
http://blog.csdn.net/u013236946/article/details/72871858
http://www.cnblogs.com/cjnmy36723/p/7018860.html