无线定位原理:TOA & AOA
无线定位原理:TOA&AOA
TOA 定位方法
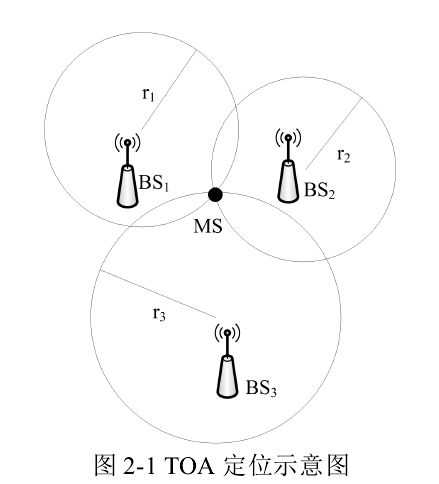
TOA 定位方法,主要是根据测量接收信号在基站和移动台之间的到达时间,然后转换为距离,从而进行定位。该方法至少需要三个基站,才能计算目标的位置,其定位示意图如图所示。
三个基站测得与 MS 的距离分别为 r 1 , r 2 , r 3 r_1,r_2,r_3 r1,r2,r3,以各自基站为圆心测量距离为半径,绘制三个圆,其交点即为 MS 的位置。当三个基站都是 LOS 基站时,一般可以根据最小二乘(LS)算法计算 MS 的估计位置。假设 MS 位的置坐标为 ( x , y ) (x,y) (x,y), N N N 个 BS 的位置坐标为 ( x i , y i ) (x_i,y_i) (xi,yi),根据其几何意义,则它们之间满足的关系是
( x i − x ) 2 + ( y − y i ) 2 = r i 2 , i = 1 , 2 , ⋯ , N (x_i-x)^2+(y-y_i)^2=r_i^2,\quad i=1,2,\cdots,N (xi−x)2+(y−yi)2=ri2,i=1,2,⋯,N
将公式展开,化简得到
x i 2 + y i 2 + x 2 + y 2 − 2 x i x − 2 y i y = r i 2 ⇓ K i = x i 2 + y i 2 , R = x 2 + y 2 ⇓ r i 2 − K i = − 2 x i x − 2 y i y + R ⇓ [ r 1 2 − K 1 r 2 2 − K 2 ⋮ r N 2 − K N ] = [ − 2 x 1 − 2 y 1 1 − 2 x 2 − 2 y 2 1 ⋮ − 2 x N − 2 y N 1 ] [ x y R ] ⇓ Y = A X x_i^2+y_i^2+x^2+y^2-2x_ix-2y_iy=r_i^2 \\ \Downarrow \\ K_i = x_i^2+y_i^2,\quad R=x^2+y^2 \\ \Downarrow \\ r_i^2-K_i=-2x_ix-2y_iy+R \\ \Downarrow \\ \begin{bmatrix} r_1^2-K_1\\ r_2^2-K_2\\ \vdots \\ r_N^2-K_N \end{bmatrix} = \begin{bmatrix} -2x_1&-2y_1&1\\ -2x_2&-2y_2&1\\ \vdots \\ -2x_N&-2y_N&1 \end{bmatrix} \begin{bmatrix} x\\ y\\ R \end{bmatrix} \\ \Downarrow \\ Y=AX xi2+yi2+x2+y2−2xix−2yiy=ri2⇓Ki=xi2+yi2,R=x2+y2⇓ri2−Ki=−2xix−2yiy+R⇓⎣⎢⎢⎢⎡r12−K1r22−K2⋮rN2−KN⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡−2x1−2x2⋮−2xN−2y1−2y2−2yN111⎦⎥⎥⎥⎤⎣⎡xyR⎦⎤⇓Y=AX
我们要求得坐标 ( x , y ) (x,y) (x,y),即求得 X X X。利用最小二乘法可得
X = ( A T A ) − 1 A T Y X = (A^TA)^{-1}A^TY X=(ATA)−1ATY
AOA 定位方法
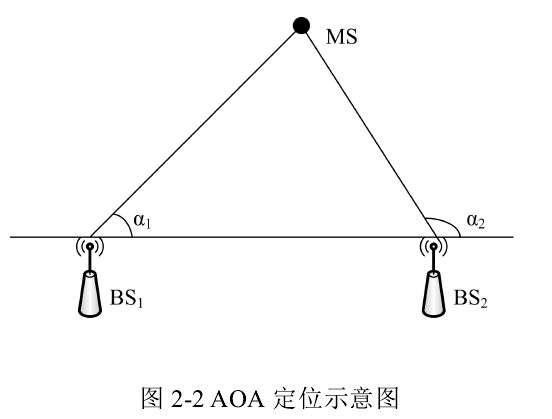
AOA 定位方法,主要是测量信号移动台和基站之间的到达角度,以基站为起点形成的射线必经过移动台,两条射线的交点即为移动台的位置。该方法只需两个基站就可以确定 MS 的估计位置,其定位示意图如图所示。
当 BS 装有天线阵列时,天线阵列根据移动台发送的信号来确定入射角度。两个基站的入射角分别为 α 1 , α 2 \alpha_1,\alpha_2 α1,α2,以各基站为起点,入射角方向构造直线的交点,即为 MS 的位置。假设 MS 位的置坐标为 ( x , y ) (x,y) (x,y), N N N 个 BS 的位置坐标为 ( x i , y i ) (x_i,y_i) (xi,yi),根据其几何意义,则它们之间满足
tan α i = y − y i x − x i \color{red} { \tan \alpha_i = \frac{y-y_i}{x-x_i} } tanαi=x−xiy−yi
将上式展开可得
( x − x i ) tan α i = y − y i ⇓ y i − x i tan α i = − x tan α i + y ⇓ [ y 1 − x 1 tan α 1 y 2 − x 2 tan α 2 ⋮ y N − x N tan α N ] = [ − tan α 1 1 − tan α 2 1 ⋮ − tan α N 1 ] [ x y ] ⇓ Y = A X (x-x_i)\tan \alpha_i = y-y_i \\ \Downarrow \\ y_i-x_i\tan \alpha_i = -x\tan \alpha_i+y \\ \Downarrow \\ \begin{bmatrix} y_1-x_1\tan \alpha_1\\ y_2-x_2\tan \alpha_2\\ \vdots \\ y_N-x_N\tan \alpha_N \end{bmatrix} = \begin{bmatrix} -\tan \alpha_1&1\\ -\tan \alpha_2&1\\ \vdots \\ -\tan \alpha_N&1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} \\ \Downarrow \\ Y=AX (x−xi)tanαi=y−yi⇓yi−xitanαi=−xtanαi+y⇓⎣⎢⎢⎢⎡y1−x1tanα1y2−x2tanα2⋮yN−xNtanαN⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡−tanα1−tanα2⋮−tanαN111⎦⎥⎥⎥⎤[xy]⇓Y=AX
同样可以利用最小二乘法解的 X X X。
TOA/AOA 混合定位
当基站能同时获得 TOA 和 AOA 信息时,通常联合上述公式,采用 TOA/AOA 混合定位方法,令
Y = [ r 1 2 − K 1 ⋮ r N 2 − K N y 1 − x 1 tan α 1 ⋮ y N − x N tan α N ] A = [ − 2 x 1 − 2 y 1 1 ⋮ − 2 x N − 2 y N 1 − tan α 1 1 0 ⋮ − tan α N 1 0 ] X = [ x y R ] \begin{aligned} Y &= \begin{bmatrix} r_1^2-K_1\\ \vdots \\ r_N^2-K_N \\ y_1-x_1\tan \alpha_1\\ \vdots \\ y_N-x_N\tan \alpha_N \end{bmatrix} \\ A &= \begin{bmatrix} -2x_1&-2y_1&1\\ \vdots \\ -2x_N&-2y_N&1\\ -\tan \alpha_1&1&0\\ \vdots \\ -\tan \alpha_N&1&0 \end{bmatrix} \\ X &= \begin{bmatrix} x\\ y\\ R \end{bmatrix} \end{aligned} YAX=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡r12−K1⋮rN2−KNy1−x1tanα1⋮yN−xNtanαN⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡−2x1⋮−2xN−tanα1⋮−tanαN−2y1−2yN111100⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎡xyR⎦⎤
同理利用 LS 算法求解,得到移动台的位置。