回归（python代码案例+图展示）

回归：从大量的结果和自变量反推函数表达式的过程就是回归

而回归的过程通常采用拟合的方法（找函数）来实现。

拟合可能出现过拟合和欠拟合：

过拟合的危害：（1）描述复杂   （2）泛化能力差

              原因： （1）训练样本少  （2）力求完美

欠拟和的原因：（1）参数过少导致模型不准确

                         （2）拟合方法不当导致模型太差

 

=======================================================================================

#!/usr/bin/env python
# encoding: utf-8
""

@Company：华中科技大学电气学院聚变与等离子实验室
@version: V1.0
@author: YEXIN
@contact: [email protected] 2018--2020
@software: PyCharm
@file: Regession2.py
@time: 2018/8/14 10:39
@Desc：线性回归的案例，详细求解a，b
"""
import numpy as np
import matplotlib.pyplot as plt

#原始数据
x = [1,2,3,4,5,6,7,8,9]
y = [0.199,0.389,0.580,0.783,0.980,1.177,1.382,1.575,1.771]

t1 = t2 = t3 = t4 = 0
n =  len(x)
for i in range(n):
    ###求和
    t1 += y[i]
    t2 += x[i]
    t3 += y[i]*x[i]
    t4 += x[i]**2

a = (t1*t2/n -t3) / (t2**2/n -t4)
b = (t1 - a*t2)/n

x = np.array(x)
y = np.array(y)

##画图
plt.plot(x,y,'o',label = "Original data",markersize = 8)
plt.plot(x,a*x + b,'r',label = '拟合曲线')
plt.show()
print(a,b)

======================================================================================

#!/usr/bin/env python
# encoding: utf-8
"""

@Company：华中科技大学电气学院聚变与等离子研究所

@version: V1.0
@author: YEXIN
@contact: [email protected] 2018--2020
@software: PyCharm
@file: Regression_Line.py
@time: 2018/8/14 9:48
@Desc：线性回归的案例
"""
import numpy as np
import matplotlib.pyplot as plt

#原始数据
x = [1,2,3,4,5,6,7,8,9]
y = [0.199,0.389,0.580,0.783,0.980,1.177,1.382,1.575,1.771]

A = np.vstack([x,np.ones(len(x))]).T  #B.T表示取B的转置

#调用最小二乘法函数
a, b = np.linalg.lstsq(A,y,rcond=-1)[0]

#转换成numpy array
x = np.array(x)
y = np.array(y)

print(a,b)

#画图
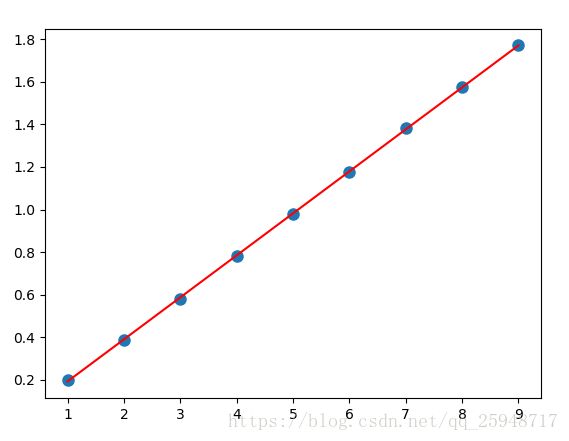
plt.plot(x,y,'o',label = "Original data",markersize = 8)
plt.plot(x,a*x + b,'r',label = '拟合曲线')
plt.show()

print(a,b)