Kaggle入门之泰坦尼克号生还率预测

这是Kaggle上的一道入门题目，旨在让我们了解机器学习的大致过程。
题目链接： Titanic: Machine Learning from Disaster
题目大意：当年泰坦尼克号的沉没造成了很多人的死亡，救生艇不足是造成如此多人死亡的主要原因。尽管能否活下来要看运气，但是有些群体的存活概率比其他人更高。现在给出一些乘客的信息，包括他最后是否生还。根据这些信息，我们要对其他乘客是否生还进行预测。
首先引入我们需要的模块，如numpy、pandas和sklearn等：

import numpy as np
import pandas as pd
from pandas import Series, DataFrame

import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import Imputer

然后，通过pandas读取训练数据并查看前5条数据：

train_data = pd.read_csv('./data/train.csv')
train_data.head()

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.0	1	0	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th…	female	38.0	1	0	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.0	0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	0	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	male	35.0	0	0	373450	8.0500	NaN	S

可以看到，整个数据集一共有12列，根据描述，每一列的含义如下：

列名	含义
PassengerId	乘客编号
Survival	是否生还，0表示未生还，1表示生还
Pclass	船票种类，折射处乘客的社会地位，1表示上层阶级，2表示中层阶级，3表示底层阶级
Sex	性别，男性为male，女性为female
Age	年龄，不满1岁的年龄为小数
SibSp	该乘客同船的兄弟姐妹及配偶的数量
Parch	该乘客同船的父母以及儿女的数量
Ticket	船票编号
Fare	买票的费用
Cabin	船舱编号
Embarked	代表在哪里上的船

下面我们看一下数据的描述性统计结果：

train_data.describe()

	PassengerId	Survived	Pclass	Age	SibSp	Parch	Fare
count	891.000000	891.000000	891.000000	714.000000	891.000000	891.000000	891.000000
mean	446.000000	0.383838	2.308642	29.699118	0.523008	0.381594	32.204208
std	257.353842	0.486592	0.836071	14.526497	1.102743	0.806057	49.693429
min	1.000000	0.000000	1.000000	0.420000	0.000000	0.000000	0.000000
25%	223.500000	0.000000	2.000000	20.125000	0.000000	0.000000	7.910400
50%	446.000000	0.000000	3.000000	28.000000	0.000000	0.000000	14.454200
75%	668.500000	1.000000	3.000000	38.000000	1.000000	0.000000	31.000000
max	891.000000	1.000000	3.000000	80.000000	8.000000	6.000000	512.329200

根据描述性统计结果，我们知道一共有891条记录，Age这一列有100多个缺失值。可以看到船上这些人的平均年龄在29岁左右，年龄最小的不到半岁，年龄最大的则有80岁。另外，船票的价格差距也比较大，有的人没有付钱就上了船，而船费最高的人则有512，而平均船费为32左右，这里猜测一下船费和最后是否生还有较大的关系。
下面我们进行探索性数据分析。首先看一下性别和是否生还之间的关系：

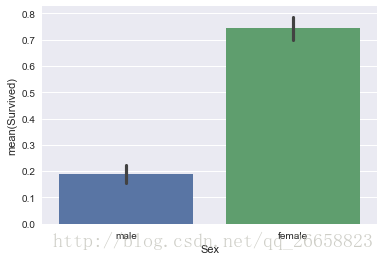
sns.barplot(x='Sex',y='Survived',data=train_data)

可以看出，男性的平均生还率不到0.2，而女性的平均生还率在0.75左右，说明性别对是否生还有着重大影响。下面我们再看一下登船地点是否会对生还率产生影响：

sns.barplot(x='Embarked',y='Survived',hue='Sex',data=train_data)

图片显示，在C地登船的人比在其他地方登船的人的平均生还率高，在Q地登船的男性生还率最低。这说明登船地点对是否生还有一定的影响，可以把它当作一个特征。接着，我们看一下社会地位对平均生还率的影响：

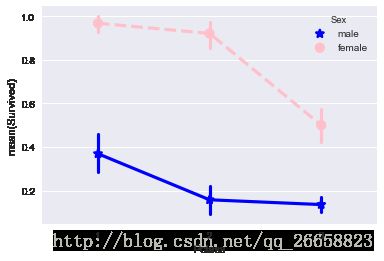
sns.pointplot(x='Pclass',y='Survived',hue='Sex',data=train_data,
             palette={'male':'blue','female':'pink'},
             markers=['*','o'],linestyles=['-','--'])

图片显示，上层阶级男性与女性的生还率均比其他两个阶级高。对女性来说，中上层阶级的平均生还率比下层阶级女性高；而对于男性，中下层阶级的平均生还率没有很大的差别，上层阶级的平均生还率则明显高于其他两个阶级。因此，社会地位可以作为一个特征用来预测生还率。我记得《泰坦尼克号》中有一句台词：“让女人和孩子先走”，所以这里猜测年龄对生还有较大的影响。下面看一下各年龄段男女的生还人数：

grid = sns.FacetGrid(train_data,col='Survived',row='Sex',
                    size=2.2,aspect=1.6)
grid.map(plt.hist,'Age',alpha=.5,bins=20)
grid.add_legend()

train_data.Sex.value_counts()

male      577
female    314
Name: Sex, dtype: int64

船上共有男性577名，女性314名，男性的人数大约为女性人数的1.8倍 。在上面四幅图片中，可以明显看到，20岁到60岁的人中间，男性未生还的人数明显多于女性。“让女人和孩子先走”这一句台词在图中也有所体现，0~5岁儿童的生还率比较高。

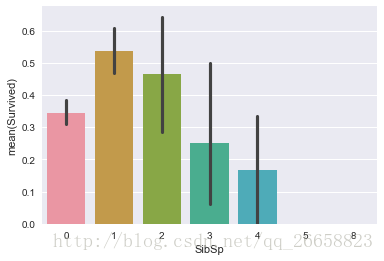
sns.barplot(x='SibSp',y='Survived',data=train_data)

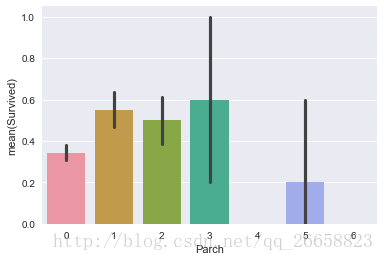
有1个和2个兄弟或配偶时比没有兄弟和配偶时的生还几率要高，这也是人之常情，毕竟碰到困难的时候都会与自己关系好的人汇合。但是随着兄弟或配偶的增多，生还几率越来越低，毕竟人越多，一旦有一个人出了问题，一群人都要等那个人。下面对Parch的分析也基本类似。

sns.barplot(x='Parch',y='Survived',data=train_data)

下面我们对数据进行一些处理，首先要将年龄的缺失值补全，这里我们用年龄的中位数来填充缺失值：

train_data.Age = train_data.Age.fillna(train_data.Age.median())
train_data.describe()

	PassengerId	Survived	Pclass	Age	SibSp	Parch	Fare
count	891.000000	891.000000	891.000000	891.000000	891.000000	891.000000	891.000000
mean	446.000000	0.383838	2.308642	29.361582	0.523008	0.381594	32.204208
std	257.353842	0.486592	0.836071	13.019697	1.102743	0.806057	49.693429
min	1.000000	0.000000	1.000000	0.420000	0.000000	0.000000	0.000000
25%	223.500000	0.000000	2.000000	22.000000	0.000000	0.000000	7.910400
50%	446.000000	0.000000	3.000000	28.000000	0.000000	0.000000	14.454200
75%	668.500000	1.000000	3.000000	35.000000	1.000000	0.000000	31.000000
max	891.000000	1.000000	3.000000	80.000000	8.000000	6.000000	512.329200

然后，我们把性别处理成数字，让男性为1，女性为0：

train_data.Sex.unique()

array(['male', 'female'], dtype=object)

train_data.loc[train_data.Sex == 'male','Sex'] = 1
train_data.loc[train_data.Sex == 'female','Sex'] = 0
train_data.head()

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	1	22.0	1	0	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th…	0	38.0	1	0	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	0	26.0	0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	0	35.0	1	0	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	1	35.0	0	0	373450	8.0500	NaN	S

接着处理登船地点，由于登船地点有缺失值，所以我们要将缺失值补全。因为在S地登船的人最多，所以我们猜测确实的那部分数据中S出现的次数应该是比较多的，这里就用S去填充缺失值。然后把这一列转化成数值型数据：

train_data.Embarked.unique()

array(['S', 'C', 'Q', nan], dtype=object)

train_data.Embarked.value_counts()

S    644
C    168
Q     77
Name: Embarked, dtype: int64

train_data.Embarked = train_data.Embarked.fillna('S')
train_data.loc[train_data.Embarked == 'S','Embarked'] = 0
train_data.loc[train_data.Embarked == 'C','Embarked'] = 1
train_data.loc[train_data.Embarked == 'Q','Embarked'] = 2
train_data.head()

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	1	22.0	1	0	A/5 21171	7.2500	NaN	0
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th…	0	38.0	1	0	PC 17599	71.2833	C85	1
2	3	1	3	Heikkinen, Miss. Laina	0	26.0	0	0	STON/O2. 3101282	7.9250	NaN	0
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	0	35.0	1	0	113803	53.1000	C123	0
4	5	0	3	Allen, Mr. William Henry	1	35.0	0	0	373450	8.0500	NaN	0

数据处理完毕后，我们就可以根据选择出的特征来训练模型了。由于这是一个二分类的问题，所以我们这里用Logistic回归算法：

features = ['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked']

alg = LogisticRegression()
kf = KFold(n_splits=5, random_state=1)
predictions = list()
for train, test in kf.split(train_data):
    k_train = train_data[features].iloc[train,:]
    k_label = train_data.Survived.iloc[train]
    alg.fit(k_train,k_label)
    k_predictions = alg.predict(train_data[features].iloc[test,:])
    predictions.append(k_predictions)

predictions = np.concatenate(predictions,axis=0)
accuracy_score(train_data.Survived,predictions)

0.79349046015712688

可以看到，使用Logistic回归预测的结果接近80%，效果还不错。
下面我们就处理我们需要预测的数据，然后使用训练数据对它进行预测。

test_data = pd.read_csv('./data/test.csv')
test_data.head()

	PassengerId	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	892	3	Kelly, Mr. James	male	34.5	0	0	330911	7.8292	NaN	Q
1	893	3	Wilkes, Mrs. James (Ellen Needs)	female	47.0	1	0	363272	7.0000	NaN	S
2	894	2	Myles, Mr. Thomas Francis	male	62.0	0	0	240276	9.6875	NaN	Q
3	895	3	Wirz, Mr. Albert	male	27.0	0	0	315154	8.6625	NaN	S
4	896	3	Hirvonen, Mrs. Alexander (Helga E Lindqvist)	female	22.0	1	1	3101298	12.2875	NaN	S

test_data.describe()

	PassengerId	Pclass	Age	SibSp	Parch	Fare
count	418.000000	418.000000	332.000000	418.000000	418.000000	417.000000
mean	1100.500000	2.265550	30.272590	0.447368	0.392344	35.627188
std	120.810458	0.841838	14.181209	0.896760	0.981429	55.907576
min	892.000000	1.000000	0.170000	0.000000	0.000000	0.000000
25%	996.250000	1.000000	21.000000	0.000000	0.000000	7.895800
50%	1100.500000	3.000000	27.000000	0.000000	0.000000	14.454200
75%	1204.750000	3.000000	39.000000	1.000000	0.000000	31.500000
max	1309.000000	3.000000	76.000000	8.000000	9.000000	512.329200

test_data.Age = test_data.Age.fillna(test_data.Age.mean())
test_data.head()

	PassengerId	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	892	3	Kelly, Mr. James	male	34.5	0	0	330911	7.8292	NaN	Q
1	893	3	Wilkes, Mrs. James (Ellen Needs)	female	47.0	1	0	363272	7.0000	NaN	S
2	894	2	Myles, Mr. Thomas Francis	male	62.0	0	0	240276	9.6875	NaN	Q
3	895	3	Wirz, Mr. Albert	male	27.0	0	0	315154	8.6625	NaN	S
4	896	3	Hirvonen, Mrs. Alexander (Helga E Lindqvist)	female	22.0	1	1	3101298	12.2875	NaN	S

test_data.loc[test_data.Sex == 'male', 'Sex'] = 1
test_data.loc[test_data.Sex == 'female', 'Sex'] = 0
test_data.head()

	PassengerId	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	892	3	Kelly, Mr. James	1	34.5	0	0	330911	7.8292	NaN	Q
1	893	3	Wilkes, Mrs. James (Ellen Needs)	0	47.0	1	0	363272	7.0000	NaN	S
2	894	2	Myles, Mr. Thomas Francis	1	62.0	0	0	240276	9.6875	NaN	Q
3	895	3	Wirz, Mr. Albert	1	27.0	0	0	315154	8.6625	NaN	S
4	896	3	Hirvonen, Mrs. Alexander (Helga E Lindqvist)	0	22.0	1	1	3101298	12.2875	NaN	S

test_data.Embarked = test_data.Embarked.fillna('S')
test_data.loc[test_data.Embarked == 'S','Embarked'] = 0
test_data.loc[test_data.Embarked == 'C','Embarked'] = 1
test_data.loc[test_data.Embarked == 'Q','Embarked'] = 2
test_data.describe()

	PassengerId	Pclass	Age	SibSp	Parch	Fare
count	418.000000	418.000000	418.000000	418.000000	418.000000	417.000000
mean	1100.500000	2.265550	30.272590	0.447368	0.392344	35.627188
std	120.810458	0.841838	12.634534	0.896760	0.981429	55.907576
min	892.000000	1.000000	0.170000	0.000000	0.000000	0.000000
25%	996.250000	1.000000	23.000000	0.000000	0.000000	7.895800
50%	1100.500000	3.000000	30.272590	0.000000	0.000000	14.454200
75%	1204.750000	3.000000	35.750000	1.000000	0.000000	31.500000
max	1309.000000	3.000000	76.000000	8.000000	9.000000	512.329200

test_data[features] = Imputer().fit_transform(test_data[features])
alg = LogisticRegression()
kf = KFold(n_splits=5,random_state=1)
for train, test in kf.split(train_data):
    k_train = train_data[features].iloc[train,:]
    k_label = train_data.Survived.iloc[train]
    alg.fit(k_train,k_label)
predictions = alg.predict(test_data[features])

预测完毕之后，我们将结果写入到一个CSV文件中，提交并查看结果。

df = DataFrame([test_data.PassengerId,Series(predictions)],index=['PassengerId','Survived'])
df.T.to_csv('./data/gender_submission.csv',index=False)

本文GitHub地址：Litt1e0range/Kaggle/Titanic