【Graph Embedding】LINE:大规模信息网络的嵌入方法
今天的这篇论文是 MSRA 2015 年的工作——《LINE: Large-scale Information Network Embedding》,截至目前共有 1900 多引用,主要的是如何在大尺度网络中应用 Embedding 技术。
1. Introduction
之前介绍的 DeepWalk 采用分布式并行方式来训练模型,但如果在硬件资源有限的条件下该如何训练出一个拥有百万结点和数十亿条边的网络呢?针对这种情况,MSRA 的同学们提出了一种可以应用于这种大规模网络计算的新型算法——LINE。LINE 适用于任何类型的网络结构,无论是有向图还是无向图,以及是否加权(DeepWalk 只适用于有向网络)。LINE 能够在单台服务器上训练数小时即可完成数百万结点和数十亿条边的网络训练。
2. LINE
2.1 First-order
很多 NetWork Embedding 算法只观察到了节点的链路表示,这种关系只具有 first-order 相似性,并没有捕捉到节点间更多的关系。这篇论文将在 first-order 的基础上探讨节点的 second-order 相似性。
second-order 并不是通过节点间的连接强弱来判定的,而是通过节点的共享邻域结构来确定的。作者通过利用节点的共享邻居来评估节点的相似性,这个想法来源于社会学和语言学,比如说:拥有很多共同朋友的人很可能有共同的兴趣从而很有可能成为朋友(现在不是朋友不代表以后不是朋友),与很多相似的单词一起使用的两个单词更可能有相似的含义。
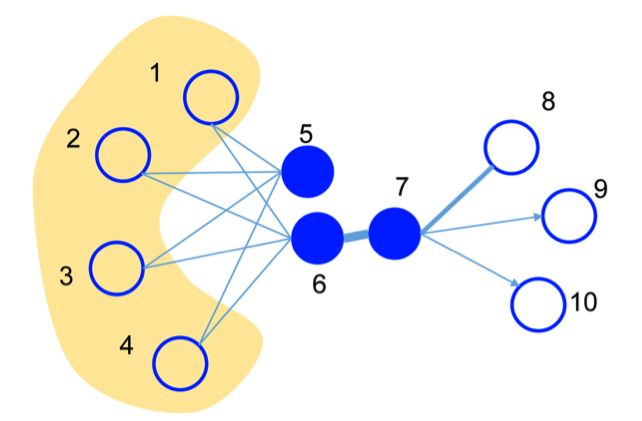
以下图为例:
- 节点 6 和 7 之间由于权值比较大, 所以具有较高的 first-order ,他们的 Embedding 向量距离会比较近;
- 另一方面节点 5 和 6 虽然没有联系,但他们有许多共同的邻居,所以较高的 second-order ,因此他们的 Embedding 向量也应该有较近的距离。
有了感性的认识后,我们给出具体定义。
first-order 是指网络中节点之间的局部连接,对每条无向边进行建模,我们给出联合概率:
p 1 ( v i , v j ) = 1 1 + e x p ( − u i T , u j ) p_1(v_i,v_j) = \frac{1}{1+exp(-u_i^T,u_j)} \\ p1(vi,vj)=1+exp(−uiT,uj)1
其中, v i v_i vi 表示节点 i, u i u_i ui 为节点 i 对应的 Embedding 向量。
根据网络权值,我们的也有经验分布为:
p 1 ^ ( i , j ) = w i j W \hat{p_1}(i,j) = \frac{w_{ij}}{W} \\ p1^(i,j)=Wwij
其中, w i j w_{ij} wij 为节点 i 和结点 j 之间的权值,W 为网络总权值之和。
为了保证一阶性,我们只需要让经验分布和联合概率分布的越相似越好,衡量两个分布差异的指标为 KL 散度,忽略常数后我们有代价函数:
m i n i m i z e O 1 = − ∑ ( i , j ) ∈ E w i j l o g ( p 1 ( v i , v j ) ) minimize \; O_1 = -\sum_{(i,j)\in E}w_{ij}log\big(p_1(v_i, v_j)\big) \\ minimizeO1=−(i,j)∈E∑wijlog(p1(vi,vj))
这里,first-order 的目标函数只适用于无向图,不适用于有向图,因为我们用的是无向边。
2.2 Second-order
second-order 适用于无向图也适用于有向图,second-order 是通过假设两个节点共享着许多与其他节点的连接(共享邻域),这种情况下也可以被视为具有相似的上下文。
我们给出节点间共现的概率为:
p 2 ( v j ∣ v i ) = e x p ( u j ′ T , u i ) ∑ k = 1 ∣ V ∣ e x p ( u k ′ T , u i ) p_2(v_j|v_i) = \frac{exp(u_j^{'T}, u_i)}{\sum_{k=1}^{|V|}exp(u_k^{'T}, u_i)} \\ p2(vj∣vi)=∑k=1∣V∣exp(uk′T,ui)exp(uj′T,ui)
其中, u i u_i ui 表示节点 i 的 Embedding 向量, u j ′ u_j^{'} uj′ 表示节点 j 为上下文时的 Embedding 向量,|V| 表示上下文节点的数量。
如上所述,second-order 假设在上下文中具有相似分布的顶点彼此相似。
second-order 经验分布定义为:
p ^ 2 ( v j ∣ v i ) = w i j d e g r e e i \hat p_2(v_j|v_i)=\frac{w_{ij}}{degree_i} \\ p^2(vj∣vi)=degreeiwij
其中, w i j w_{ij} wij 为边的权重, d e g r e e i degree_i degreei 为节点 i 的度数, d e g r e e i = ∑ j ∈ N ( i ) w i k degree_i = \sum_{j\in N(i)} w_ik degreei=∑j∈N(i)wik, N ( i ) N(i) N(i) 为节点 i 的邻居。
为了保证 second-order,我们需要让条件概率分布 p 2 ( ⋅ ∣ v i ) p_2(\cdot|v_i) p2(⋅∣vi) 与经验分布 p ^ 2 ( ⋅ ∣ v i ) \hat p_2(\cdot|v_i) p^2(⋅∣vi) 相似。因此我们有:
m i n i m i z e O 2 = − ∑ i ∈ V λ i d ( p ^ 2 ( ⋅ ∣ v i ) , p 2 ( ⋅ ∣ v j ) ) minimize \; O_2 = -\sum_{i\in V}\lambda_i d\big(\hat p_2(\cdot|v_i),\; p_2(\cdot| v_j)\big) \\ minimizeO2=−i∈V∑λid(p^2(⋅∣vi),p2(⋅∣vj))
其中, d ( ⋅ , ⋅ ) d(\cdot,\cdot) d(⋅,⋅) 表示两个分布的距离; λ i \lambda_i λi 表示节点的重要性,可以通过类似 PageRank 算法得到。
接着用 KL 散度来代替 d ( ⋅ , ⋅ ) d(\cdot , \cdot) d(⋅,⋅) 来衡量两个分布的相似性。为简单起见,我们令 λ i = d e g r e e i \lambda_i = degree_i λi=degreei,所以我们有:
m i n i m i z e O 2 = − ∑ ( i , j ) ∈ E w i j l o g ( p 2 ( v j ∣ v i ) ) minimize \; O_2 = -\sum_{(i,j)\in E}w_{ij}log\big(p_2(v_j| v_i)\big) \\ minimizeO2=−(i,j)∈E∑wijlog(p2(vj∣vi))
2.3 Combing
我们希望训练的网络保留 first-order 和 second-order ,而在实践过程中作者发现了一个简单有效的方法:分别训练一阶近似和二阶近似的模型,然后将其得到的 Embedding 连接起来。
当然,作者表示更应该把两个目标函数联合起来训练,并表示这将留作以后探讨。
3. Optimization
3.1 Negative Sampling
针对目标函数求 Softmax 需要遍历所有节点这一问题,同样采用 Negative Sampling 进行优化,目标函数为:
l o g σ ( u j ′ T ⋅ u i ) + ∑ i = 1 K E n s [ l o g σ ( − u n ′ T ⋅ u i ) ] log \ \sigma(u_j^{'T} \cdot u_i) + \sum_{i=1}^K E_{ns}[log \ \sigma(-u_n^{'T}\cdot u_i)] \\ log σ(uj′T⋅ui)+i=1∑KEns[log σ(−un′T⋅ui)]
当然,涉及到稀疏参数更新,就可以利用异步随机梯度下降(Asynchronous Stochastic Gradient Algorithm, ASGD)算法进行加速。目标函数的偏导数为:
∂ O 2 ∂ u i = w i j ⋅ ∂ p 2 ( v j ∣ v i ) ∂ u i \frac{\partial O_2}{\partial u_i} = w_{ij}\cdot \frac{\partial\ p_2(v_j|v_i)}{\partial u_i} \\ ∂ui∂O2=wij⋅∂ui∂ p2(vj∣vi)
我们看到计算梯度时需要乘上边的权值,但这样会出现一个问题:
- 如果选择一个较小的学习率,对于权值较小的边可能会导致梯度消失,学习速度过慢而无法收敛;
- 而如果选择一个较大的学习率,对于权值较大的边可能会出现梯度爆炸。
所以,该如何设定一个较好的学习率以应对边的权值方差较大的现象?
3.2 Edge Sampling
一种直接的想法是:导致这种问题的原因是边的权值,如果另所有边的权值相等就不会在出现这种问题了。
因此一个简单的方法就是将一个加权边分成多个权值为 1 的二元边,例如:一个权值为 4 的边,我们可以将其分成 4 个权值为 1 的二元边。
但这样又会出现新的问题:内存开销过大。为了解决这个新的问题,作者给出新的解决方案:对原始边进行了采样,保证采样概率与原始边的权值成正比,并将采样后的边视为权值为 1 的二元边。
通过这种边采样处理,可以保证原本的代价函数不变,且又加入了边的权重信息。
关于加权采样问题,作者使用的 Alias 算法,虽然Alias 非本文重点,但是我决定还是简单介绍一下。
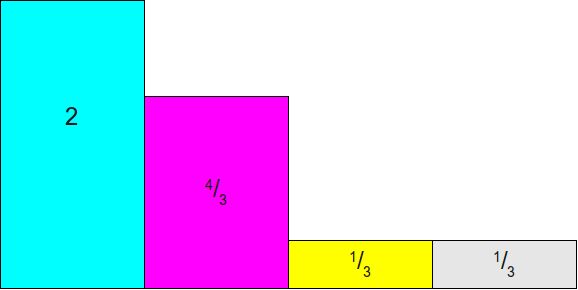
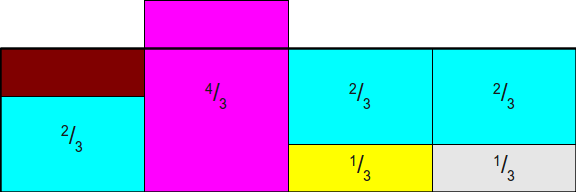
假设我们有四个权值: 1 2 , 1 3 , 1 12 , 1 12 \frac{1}{2},\frac{1}{3},\frac{1}{12},\frac{1}{12} 21,31,121,121,现在要对其进行加权采样。
区别于利用最大值进行归一化,我们基于平均值进行归一化。给出的例子的均值为 1 4 \frac{1}{4} 41,所以有:
然后我们以均值 $\frac{1}{4} $ 为高度,画出一个矩形:
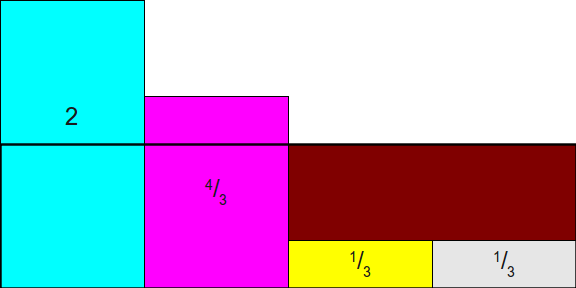
然后我们可以将多出的部分填补到空缺的部分:
现在还有两个多出来的部分,但只有一个空缺点。为了不增加开销,我们需要约束一列最多只有两个事件,所以:
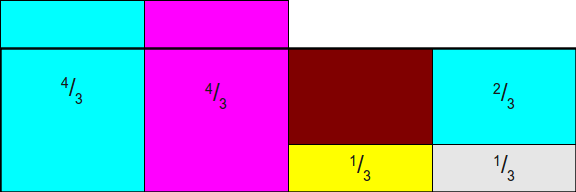
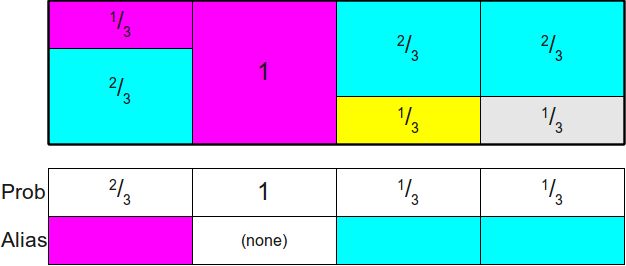
最后便产生了一个完整的矩阵:
我们来看下这个矩阵怎么使用。
我们构造两个大小相同的数组分别为概率表 Prob 和别名表 Alias,概率表为原始列在现有情况下的概率,如概率值为 $\frac{1}{2} $ 的第一列对应现在的概率值为 $\frac{2}{3} $,概率值为 $\frac{1}{3} $ 的第二列对应的现在的概率值为 1;而别名表 Alias 为多出来的另一个事件的概率,比如 Alias[0] 对应第二个事件, Alias[1] 为 None, Alias[2] 对应第一个事件,Alias[3] 也对应第一个事件。
使用方法是,先随机到某一列,然后再进行一次随机,用于判断是当前列的原本事件还是别名表 Alias 里面的另一个事件。比如我们第一次随机并得到第三列,有 Prob[2] = 1/3,然后再进行一次随机,如果随机数小于 1/3 则为事件三,如果随机数大于 1/3 则为 Alias[2] 中的别名事件,也就是事件一。
简单起见,我们省去别名表的存在性证明和生成 Alias 所采用的算法。而使用 Alias 的时间复杂度为 O(1),空间复杂度为 O(N)。
到这里,两种优化方法就介绍完成了。
4. Discussion
我们来谈论一下 LINE 模型在实际应用中的会碰到的几个问题:
- Low Degress Vertices:对于 second-order 来说,其严重依赖于节点的上下文,如果节点的度非常小,则会产生 Embedding 不充分的问题。一种解决方法是,不仅考虑邻居,而且考虑邻居的邻居,从而增加度小的节点的上下文数量;
- New Vertices:对于新的节点来说,如果其与现有节点有连接,我们可以得到其 first-order 和second-order 的经验分布,然后更新任意一个目标函数来获得其 Embedding 向量;如果不存在边连接,则需要添加额外的信息。
5. Experiment
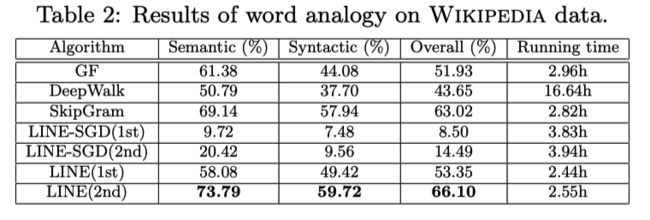
简单看一下实验
多目标情况下:
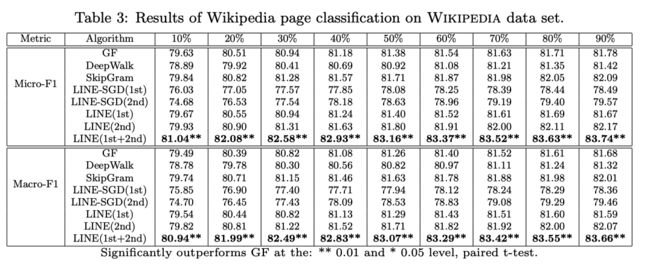
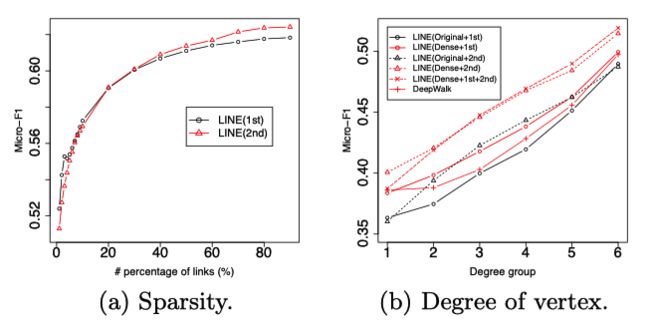
不同网络稀疏程度下(这里的稀疏性只和自己进行了比较,但我们要知道具有 second-order 相似性的节点数量比具有 first-order 相似性的节点数量要多出很多,所以 LINE 是非常适用于稀疏网络的):
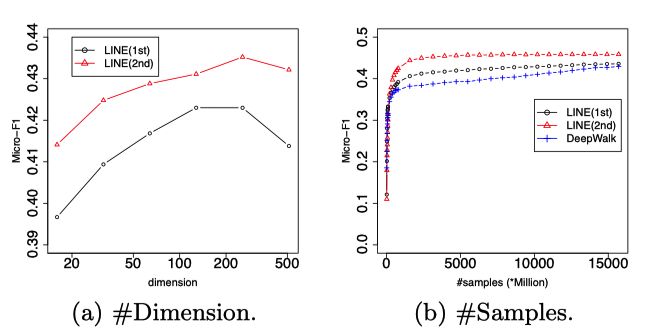
参数敏感性:
可视化结果:
6. Conclusion
总结一下 LINE:
- 通过设计两个目标函数分别约束节点的 first-order 和 second-order 相似性,使其 Embedding 向量中包含两种相似性,并通过直接拼接两个向量取得不错的效果(first-order 描述的是一种直接的关系,而 second-order 描述的更像是一种的潜在的关系);
- 算法可适用于各种类型的网络(包括加权/无权,有向/无向,稀疏/稠密),同时也适用于大尺度网络(类似的 GloVe 的训练方式,所以速度快);
- 设计了一个基于边的采样算法来优化目标函数,该算法克服了现有的随机梯度下降的局限性。
7. Reference
- 《LINE: Large-scale Information Network Embedding》
- 《Darts, Dice, and Coins: Sampling from a Discrete Distribution》
关注公众号跟踪最新内容:阿泽的学习笔记。
![]()