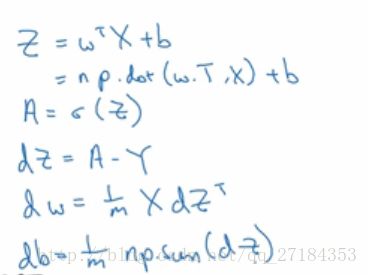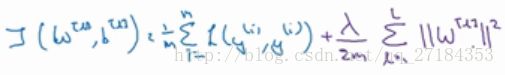吴恩达深度学习（一）

神经网络本质上 输入与输出之间的一种映射关系  一般来讲有三种 standard 神经网络（计算广告）  CNN（处理图片）  RNN（包含时间）

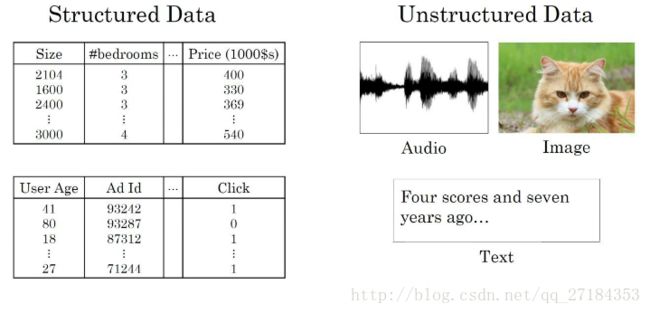
引入神经网络增强了计算机对于非结构化数据的处理能力。（图片来源于吴恩达教授深度学习之神经网络与深度学习1.3）

传统机器学习的方法 : SVM (支持向量机) 逻辑回归  开始会随着数据量增加 性能有所提升但是很快进入“平台期”，这就导致其无法处理海量数据。

要训练性能较好的神经网络，1 神经网络的规模 2 带标签的训练数据的规模（用m表示带标签的训练样本的数目）  都要适当的大

深度学习 data computation algorithm  这三者 计算能力的增强推动了深度学习的发展，如 GPU ，另外算法的改进也加快了计算的速度，如激活函数把sigmoid 改为ReLU 能够使梯度下降法运行更快。原因是sigmoid的梯度会趋于0 导致收敛很慢，但是ReLU的梯度为正整数不会出现趋于0的情况。

加快计算速度的原因是（1）即使是很大的数据规模和神经网络规模，也可以在合理的时间内完成运算（2）提高工作效率，在较短时间内完成一次idea-> code->experiment 的过程

计算机在存储一张图片时候存储的是三个矩阵 分别代表RGB  每个矩阵中每一点处的值代表在该像素点处对应的idencity value，在深度学习过程中会把这些矩阵中的值放入一个列向量中，这个列向量就是输入的特征向量 n表示输入的特征向量的维度

输入特征矩阵的列数即训练样本的个数m  最终特征矩阵的维度 n*m

sigmoid函数 用于将输出结果落在0 1 之间，例如在逻辑回归二分类问题中需要求出概率值，概率值要在0 1 之间

深度学习中 w和b一般分开来训练不放在一个矩阵当中

右上角的上标代表第i个训练样本

非凸函数的问题是可能会导致多个局部最优解

loss function 与 cost function 的区别：

loss function  对应 just single training example  对应单个训练样本 计算出单个的训练样本对应的预测值和训练值之间的差值

                       loss function 是关于预测值和估计值的函数

cost function is the cost of your parameters 对应训练样本整体  求的整个训练样本中所有单个训练样本中求出的预测值和训练值之间的差值的平均值，求和再除以训练样本总数

                        cost function 是关于 参数w b 函数  最终的目的就是找到w b 的值使得 overall cost function 的值最小

具体内容参见下面英文

做反向传播时画出计算图，用链式求导的办法，如果理不清楚，就列好表格，原来变量数值是多少，给这个数值加0.001之后，最终的cost function的值变化量为t， a与0.001的比值就是最终关于该变量的导数。

a 是逻辑回归的输出 y是ground truth label

向量化 减少代码中的for循环提高代码的效率  用一些诸如np.函数 可以实现SIMD(single instruction multiple data) 多项数据并行处理。

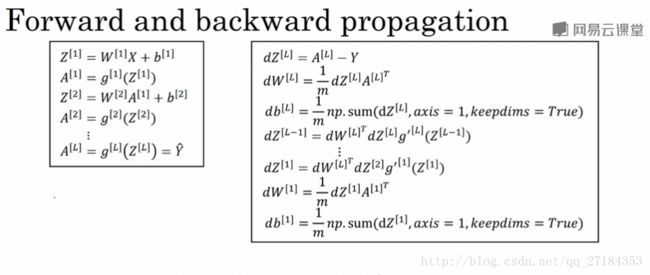
实现一个算法从两个角度 前向传播和反向传递实现。

多个值对应相乘然后做加法，可以转化成矩阵乘法

逻辑回归高度向量化之后的表示：前向传播和反向传递的过程

不太确定一个响亮的维度是多少的时候可以使用assert语句（测试assert后的condition并在condition返回结果为false的时候抛出异常）

神经网络的表示中 上角标的方括号表示第几层神经网络 下角标表示该层神经网络中的第几个结点

计算神经网络的层数时候不算输入层，输入层的序号是0 从隐含层开始算第一层第二层等等

向量化的方法  对于一个训练样本而言  对于同一层不同节点的参数w b 以行向量形式堆叠 

                      对于多个训练样本，对应不同训练样本的参数以列向量形式堆叠。

最终代表输入数据的X  横向代表不同的输入样本纵向代表同一输入样本中不同的输入特征

某层神经网络的 Z A 横向代表不同的输入样本，纵向代表该层神经网络的不同结点

一个节点处的w b 是同一个 

tanh的用处：将数据放到（-1,1之间）目的是 实现数据中心化 使得数据的平均值更加接近于0

一般情况下用tanh激活函数都优于sigmoid激活函数，sigmoid激活函数一般只用在二分类问题的输出层，因为sigmoid函数可以使得输出结果在0 1 之间。另外不同层的激活函数可以不一样所以有时候隐含层的激活函数用tanh而输出层的激活函数用sigmoid

sigmoid和tanh都有一个共同的缺点就是 当z特别大或者特别小的时候， 这两种激活函数的导数趋近于0 ，这就导致，梯度下降的速度非常慢。

ReLU函数可以解决sigmoid和tanh的上述问题。一般在隐含层如果不太确定可以使用什么激活函数，就有限选用ReLU

ReLU函数的缺点在于，当z小于0 时候，函数的导数为0 但是实际应用中z绝大多数是正值所以用ReLU时候收敛还是很快的有一种leaky ReLU（带卸扣的ReLU ）可以弥补这一问题，它在小于0 时候是一段平缓的直线

监督学习中输入x是一定的不需要对于输入x做优化，所以不对输入x进行求导

反向传播编写程序的时候确保反向传播时候的矩阵相乘是维度对应可以减少一些问题

将w b 初始化为0 存在的问题是，不同的结点完全对称计算着相同的东西

w b 随机初始化的时候选择尽可能小的值，可以在随机出来的结果后乘以0.01 。这样做的原因是如果选择sigmoid和tanh做激活函数z 太大或者太小导数都会变成0 是的收敛变慢。

w b 初始化为0 激励函数用线性函数 会导致将网络加深将神经元结点增多但是性能不再提升

深的神经网络比浅的神经网络好在哪

我现在的体会是如果是深层网络那么地阿尔戈隐含层可以在第几个隐含层处理的基础上进行进一步的处理，但是如果网络很浅，比如两层神经网络，即使有很多个hidden unit 操作的基础一直基于输入的原始数据

数据集分为train set dev set  test set  dev set用于选出哪一个模型效果较好， test set 用于评估选出来的这个模型性能如何

一般要保证 dev set 和test set come from the same distribute

过拟合 是high variance

不拟合 是high bias

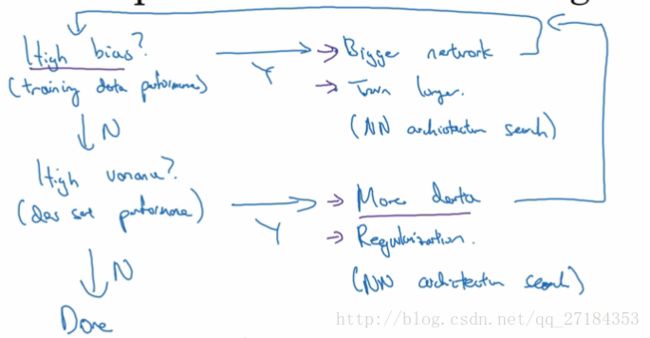
  先使用训练集训练 得到在train set 上的性能，如果此时错误率较高，为high bias ，可以通过用更大的网络或者训练更长的时间 或者选用合适的神经网络 进行调整，将错误率调整到一定区间就要在dev set上计算错误率，如果此时错误率较高为 high variance, 可能出现了过拟合的情况，可以通过使用  

更多的数据  正则化  或者 选用合适的神经网络进行调整，最终的目的是，得到low bias 和low variance的参数

L1正则化通常会得到系数矩阵 sparse

L2正则化 权重衰减 w 之前乘了一个小于1的系数

在权值矩阵之前添加惩罚值系数，避免了数据权值矩阵过大。目的在于减少部分神经元的影响，使得神经网络变得简单

原因是在使得cost 函数 J 尽可能小的时候，lamda在变大，w会变小，如果是使用tanh激活函数，则较小的w值处于tanh函数原点附近偏线性关系的部分，本身当激活函数变成线性关系时，即使加深网络对于样本的你和成都不会变好，这样就会减少一部分神经元的影响，起到防止过拟合的效果。

正则化的目的是减少过拟合，正则化的方法：L2 ， dropout

dropout 正则化可以随机删除某个节点，设置每一个节点被删除和保留的概率，删掉部分节点之后使用精简的网络进行训练

dropout的方法 invert dropout  可以确保该层神经网络的激活函数值得均值不发生改变举个例子，比如对于第三层隐含层而言，invert dropout方法可以确保a3的均值不变。因为删去节点的概率是0.2保留节点的概率是0.8，第三层隐含层删去百分之二十的节点之后剩余百分之八十，要拿a3除以百分之80  （此处的keep-prob为0.8）

使用dropout时 根据不同层的W参数多少（神经元个数多少）情况确定 不同层对应的keep-prob值，参数多（神经元多时）keep-prob值设置的偏小一些，舍弃掉比较多的神经元，参数少时，keep-prob值设置的偏大一些 。这样做可以比较好的避免过拟合但是会造成超参数的数目增多。

dropout的缺点 cost function不能被明确定义，因为每次迭代都会随机移除一部分结点。所以没有办法观察到costfunction  J 是否在下降。通常的做法是关掉dropout 的过程，就是把超参数keep-prob的值设为1 ，当观察到此时的cost function 出现下降，再打开dropout过程继续调试

防止过拟合的办法还有data argumentation 和 early stop

数据增强包括，图片的水平翻转（flip）一般不进行垂直翻转，图片的裁剪（crop） 图像的扭曲变形rotation 

early stop指的是，在J函数下降到最低点停止训练，这样做可以防止过拟合但是阻止了 J函数的进一步优化

更明知的选择初始化权重避免梯度爆炸和梯度消失

向量化处理  换激活函数（如使用ReLU）优化算法 三种办法加快梯度下降的速度

batch gradient descent一次训练整个训练集

mini batch gradient descent将整个训练集分成若干子集，每次训练只训练其中一个子集