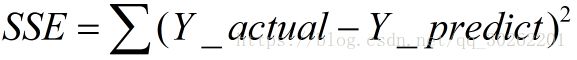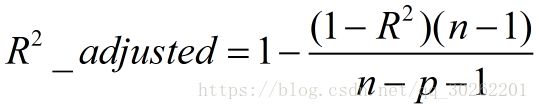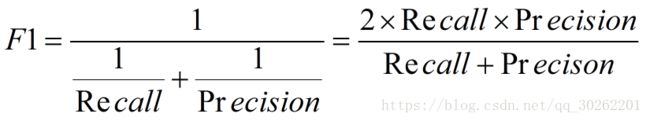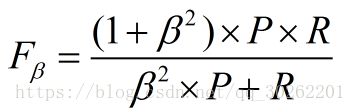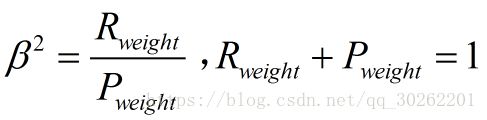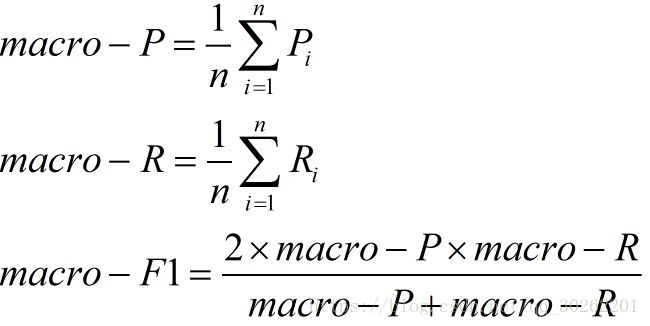搞懂回归和分类模型的评价指标的计算:混淆矩阵,ROC,AUC,KS,SSE,R-square,Adjusted R-Square
今天看到某同学总结了回归和分类模型的评价指标,两篇博客讲的特别清楚,看完后以前的疑惑都解除了,收获很大,加一点补充,整理出来方便以后查看,蓝色的大标题是原文链接。
回归模型的几个评价指标
对于回归模型效果的判断指标经过了几个过程,从SSE到R-square再到Ajusted R-square, 是一个完善的过程:
- SSE(误差平方和):The sum of squares due to error
- R-square(决定系数):Coefficient of determination
- Adjusted R-square:Degree-of-freedom adjusted coefficient of determination
下面我对以上几个名词进行详细的解释下,相信能给大家带来一定的帮助!!
一、SSE(误差平方和)
计算公式如下:
同样的数据集的情况下,SSE越小,误差越小,模型效果越好
缺点:SSE数值大小本身没有意义,随着样本增加,SSE必然增加,也就是说,不同的数据集的情况下,SSE比较没有意义
二、R-square(决定系数)
数学理解: 分母理解为原始数据的离散程度,分子为预测数据和原始数据的误差,二者相除可以消除原始数据离散程度的影响
其实“决定系数”是通过数据的变化来表征一个拟合的好坏。
- 理论上取值范围(-∞,1], 正常取值范围为[0 1] ——实际操作中通常会选择拟合较好的曲线计算R²,因此很少出现-∞
越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好
越接近0,表明模型拟合的越差
经验值:>0.4, 拟合效果好
- 缺点:数据集的样本越大,R²越大,因此,不同数据集的模型结果比较会有一定的误差
三、Adjusted R-Square (校正决定系数)
- n为样本数量,p为特征数量
- 消除了样本数量和特征数量的影响
分类模型的评价指标
对于分类模型,常用的指标有混淆矩阵、ROC曲线,AUC值,KS曲线以及KS值、Lift图,Gain图等,查阅了很多的资料,加入自己的理解整理了一下他们的计算方法和意义,希望对大家有帮助。
1. 混淆矩阵—确定截断点后,评价学习器性能
假设训练之初以及预测后,一个样本是正例还是反例是已经确定的,这个时候,样本应该有两个类别值,一个是真实的0/1,一个是预测的0/1
TP(实际为正预测为正),FP(实际为负但预测为正),TN(实际为负预测为负),FN(实际为正但预测为负)
通过混淆矩阵我们可以给出各指标的值:
查全率(召回率,recall):样本中的正例有多少被预测准确了,衡量的是查全率,预测对的正例数占真正的正例数的比率:
- 查全率=检索出的相关信息量 / 系统中的相关信息总量 = TP / (TP+FN)
查准率(精准率,Precision):针对预测结果而言,预测为正的样本有多少是真正的正样本,衡量的是查准率,预测正确的正例数占预测为正例总量的比率:
- 查准率=正确预测到的正例数/实际正例总数 = TP / (TP+FP)
准确率:反映分类器统对整个样本的判定能力,能将正的判定为正,负的判定为负的能力,计算公式:
- Accuracy=(TP+TN) / (TP+FP+TN+FN)
阴性预测值:可以理解为负样本的查准率,阴性预测值被预测准确的比例,计算公式:
- NPV=正确预测到的负例数/实际负例总数=TN / (TN+FN)
查准率和查全率通常是一对矛盾的度量,通常一个高,另外一个就低。两个指标都很重要,我们应该如何综合考虑这两个指标呢?
主要有两种办法:
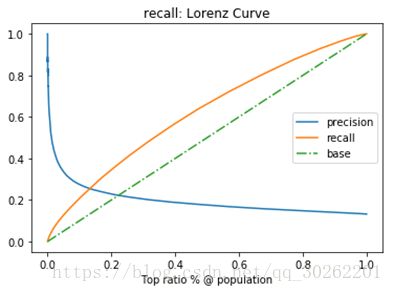
“平衡点“ Break-Even Point, BEP
查准率=查全率的点,过了这个点,查全率将增加,查准率将降低。如下图,蓝色和橘黄色的交叉点就是“平衡点”
F1度量—查准率和查全率的加权调和平均数
(1)当认为查准率和查全率一样重要时,权重相同时:
(2)当查准率查全率的重要性不同时,即权重不同时:
通常,对于不同的问题,查准率查全率的侧重不同。比如,对于商品推荐系统,为了减少对用户的干扰,查准率更重要;逃犯系统中,查全率更重要。因此,F1度量的一般形式:
其中β表示查全率与查准率的权重,很多参考书上就只给出了这个公式,那么究竟怎么推导来的呢?
两个指标的设置及其关系如下,因为只考虑这两个指标,所以二者权重和为1,即
可以推导得到。
- β=1,查全率的权重=查准率的权重,就是F1
- β>1,查全率的权重>查准率的权重
- β<1,查全率的权重<查准率的权重
那么问题又来了,如果说我们有多个二分类混淆矩阵,应该怎么评价F1指标呢?
多个二分类混淆矩阵可能有以下几种情况:多次训练/测试,多个数据集上进行训练/测试,多分类任务的两两类别组合等。
这里介绍两种做法:
(1)宏F1
设有n个混淆矩阵,计算出查全率和查准率的平均值,在计算F1即可
这种做法认为每一次的混淆矩阵(训练)是同等权重的
(2)微F1
设有n个混淆矩阵,计算出混淆矩阵对应元素(TP,FP,FN,TN)的平均值,再计算查全率、查准率,F1
这种做法认为每一个样本的权重是一样的
多分类问题的混淆矩阵怎么看?
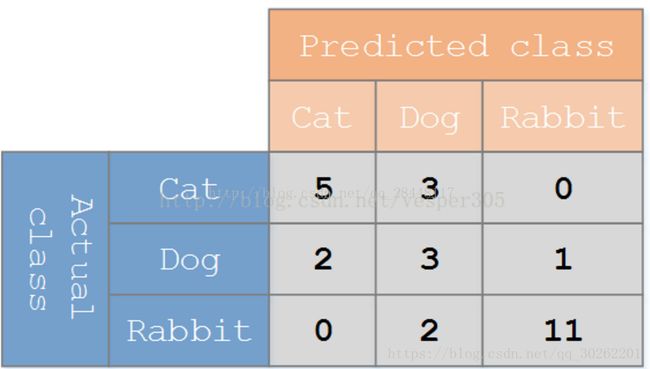
假设有一个用来对猫(cats)、狗(dogs)、兔子(rabbits)进行分类的系统,混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27 只动物:8只猫, 6条狗, 13只兔子。结果的混淆矩阵如上图:
在这个混淆矩阵中,实际有8只猫,但是系统将其中3只预测成了狗;对于6条狗,其中有1条被预测成了兔子,2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题,但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在对角线上,所以从混淆矩阵中可以很方便直观的看出哪里有错误,因为他们呈现在对角线外面。
在预测分析中,混淆表格(有时候也称为混淆矩阵),是由false positives,falsenegatives,true positives和true negatives组成的两行两列的表格。它允许我们做出更多的分析,而不仅仅是局限在正确率,对于上面的矩阵,可以表示为下面的表格:
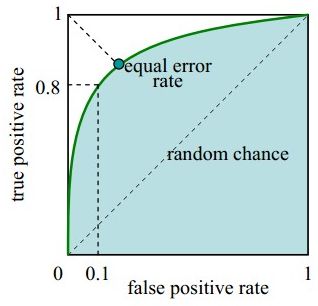
2. ROC曲线, AUC —评价学习器性能,检验分类器对客户进行正确排序的能力
分类器产生的结果通常是一个概率值不是直接的0/1变量,通常数值越到,代表正例的可能性越大。
根据任务的不同也会采取不同的“截断点”,大于则为正例,小于则为反例。如重视查全率,则阈值可以设置低一些;而重视查准率,阈值可以设置高一些。
如果设定了截断点或明确了任务,那么我们根据混淆矩阵就可以知道分类器的效果好坏。
在未设定截断点(任务不明确)情况下,我们如何评价一个分类模型的效果的好坏或者比较不同分类模型效果?
我们可以观察这个学习器利用所有可能的截断点(就是所有样本的预测结果)对样本进行分类时的效果,注意要先对所有可能的截断点进行排序,方便对比观察。
ROC曲线描绘的是不同的截断点时,并以FPR和TPR为横纵坐标轴,描述随着截断点的变小,TPR随着FPR的变化。
纵轴:TPR=正例分对的概率 = TP/(TP+FN),其实就是查全率
横轴:FPR=负例分错的概率 = FP/(FP+TN)
如果是随机分类,没有进行任何学习器,FPR=TPR,即正例分对和负例分错概率相同,预测出来的正例负例和正例负例本身的分布是一致的,所以是一条45°的直线。因此,ROC曲线越向上远离这条45°直线,说明用了这个学习器在很小的代价(负例分错为正例,横轴)下达到了相对较大的查全率(TPR)。
作图步骤:
- 根据学习器的预测结果(注意,是正例的概率值,非0/1变量)对样本进行排序(从大到小)—–这就是截断点依次选取的顺序
- 按顺序选取截断点,并计算TPR和FPR—也可以只选取n个截断点,分别在1/n,2/n,3/n等位置
- 连接所有的点(TPR,FPR)即为ROC图 例图:因为样本有限,通常不是平滑曲线
判断标准:
- 一个ROC曲线完全”包住“另一个ROC曲线—>第一个学习器效果更好
- 两个ROC曲线相交—>利用ROC曲线下的面积(AUC,area under ROC curve,是一个数值)进行比较
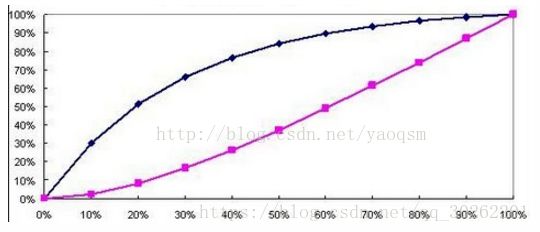
3. KS曲线,KS值—学习器将正例和反例分开的能力,确定最好的“截断点” KS曲线和ROC曲线都用到了TPR,FPR。KS曲线是把TPR和FPR都作为纵坐标,而样本数作为横坐标。
- 根据学习器的预测结果(注意,是正例的概率值,非0/1变量)对样本进行排序(从大到小)—–这就是截断点依次选取的顺序
- 按顺序选取截断点,并计算TPR和FPR —也可以只选取n个截断点,分别在1/n,2/n,3/n等位置
- 横轴为样本的占比百分比(最大100%),纵轴分别为TPR和FPR,可以得到KS曲线
- TPR和FPR曲线分隔最开的位置就是最好的”截断点“,最大间隔距离就是KS值,通常>0.2即可认为模型有比较好偶的预测准确性 例图: