Transformer的具体计算过程

Transformer中矩阵相乘的计算

假设batch_size=64,seq_len=80,d_model=512,d_ff=2048,h_head=8

1.Encoder

经过处理后的输入数据为：[batch_size,seq_len]

encoder的输入有一个[batch_size,seq_len]

<1.1>输入层

经过word embedding:[batch_size,seq_len,d_model] 这里要乘以d_model**0.5

经过positional encoding:[batch_size,seq_len,d_model]

两者相加为：[batch_size,seq_len,d_model]

数据经过dropout,为enc=[batch_size,seq_len,d_model]

<1.2>计算Multi-Head attention

输入为Q=K=V=enc=[batch_size,seq_len,d_model]

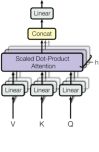
进行下图的计算

 

<1.2.1>首先进行线性运算

Q=Q*[d_model,d_model]=[batch_size,seq_len,d_model]

K=Q*[d_model,d_model]=[batch_size,seq_len,d_model]

K=Q*[d_model,d_model]=[batch_size,seq_len,d_model]

<1.2.2>进行分割

seq_len_q=seq_len_k=seq_len_v=seq_len

Q=[batch_size*h_head,seq_len_q,d_model/h_head]

K=[batch_size*h_head,seq_len_k,d_model/h_head]

V=[batch_size*h_head,seq_len_v,d_model/h_head]

<1.2.3>计算dot-product attention

 

<1.2.3.1>矩阵相乘计算

K改变形状为K=[batch_size*h_head,d_model/h_head,seq_len_k]

outputs=Q*K=

[batch_size*h_head,seq_len_q,d_model/h_head]*[batch_size*h_head,d_model/h_head,seq_len_k]=[batch_size*h_head,seq_len_q,seq_len_v]

<1.2.3.2>进行scale

d_k=Q.shape[-1]=d_model/h_head

outputs /= d_k ** 0.5

<1.2.3.3>进行mask

src_masks=[batch_size,seq_len] 是一个布尔型的矩阵，如果该位置为空(填充)，值为1

将src_masks扩展成为形状为[batch_size*h_head,seq_len]的矩阵

然后再扩展维度，得到src_masks=[batch_size*h_head,1,seq_len]

将src_masks*负无穷(-2 ** 32 + 1)

outputs=outputs+src_masks(意思是空位置的值为负无穷，在进行softmax的时候为0)

<1.2.3.4>进行softmax

outputs=softmax(outputs)

outputs=[batch_size*h_head,seq_len_q,seq_len_k]

attention=outputs转换形状=[batch_size*h_head,seq_len_k,seq_len_q]

outputs经过dropout

<1.2.3.5>最终结果相乘

outputs=outputs*V=

[batch_size*h_head,seq_len_q,seq_len_k]*[batch_size*h_head,seq_len_v,d_model/h_head]=

[batch_size*h_head,seq_len_q,d_model/h_head]

<1.2.4>进行分割连接

outputs=[batch_size,seq_len_q,d_model]

<1.2.5>进行残差连接

outputs=outputs+Q

<1.2.6>进行归一化

outputs=LayerNormer(outputs)=[batch_size,seq_len_q,d_model]

<1.3>接着计算全连接神经网络

 

<1.3.1>矩阵相乘

inputs=outputs

outputs=[batch_size,seq_len_q,d_model]*[d_model,d_ff]=[batch_size,seq_len_q,d_ff]

outputs=relu(outputs)

outputs=[batch_size,seq_len_q,d_ff]*[d_ff,d_model]=[batch_size,seq_len_q,d_model]

<1.3.2>进行残差连接

outputs=outputs+inputs

<1.3.3>进行归一化

outputs=LayerNormer(outputs)=[batch_size,seq_len_q,d_model]

这样一层的计算就完成了，后面的每一层以outputs为输入继续进行计算

得到最终的结果为outputs=[batch_size,seq_len_q,d_model]

2.Decoder

<2.1>输入层

decoder的输入有两个,大小都为[batch_size,seq_len]

(一个包含不包含，另一个包含不包含)

(这里的seq_len和encoder的不一定相同)

这里的输入使用包含不包含的输入

数据经过word embedding:[batch_size,seq_len,d_model] 这里乘以 d_model**0.5

数据经过positional encoding:[batch_size,seq_len,d_model]

两者相加：dec=[batch_size,seq_len,d_model]

<2.2>计算Masked Multi-Head Attention

输入为Q=K=V=dec=[batch_size,seq_len,d_model]

<2.2.1>首先进行线性运算

Q=Q*[d_model,d_model]=[batch_size,seq_len,d_model]

K=Q*[d_model,d_model]=[batch_size,seq_len,d_model]

K=Q*[d_model,d_model]=[batch_size,seq_len,d_model]

<2.2.2>进行分割

这里的seq_len_q=seq_len_k=seq_len_v=seq_len

Q=[batch_size*h_head,seq_len_q,d_model/h_head]

K=[batch_size*h_head,seq_len_k,d_model/h_head]

V=[batch_size*h_head,seq_len_v,d_model/h_head]

<2.2.3>计算dot-product attention

<2.2.3.1>矩阵相乘

K改变形状为K=[batch_size*h_head,d_model/h_head,seq_len_k]

outputs=Q*K=

[batch_size*h_head,seq_len_q,d_model/h_head]*[batch_size*h_head,d_model/h_head,seq_len_k]=[batch_size*h_head,seq_len_q,seq_len_v]

<2.2.3.2>进行scale

d_k=Q.shape[-1]=d_model/h_head

outputs /= d_k ** 0.5

<2.2.3.3>进行mask

首先进行padding mask

tgt_masks=[batch_size,seq_len] 是一个布尔型的矩阵，如果该位置为空(填充)，值为1

将tgt_masks扩展成为形状为[batch_size*h_head,seq_len]的矩阵

然后再扩展维度，得到tgt_masks=[batch_size*h_head,1,seq_len]

将tgt_masks*负无穷(-2 ** 32 + 1)

outputs=outputs+tgt_masks(意思是空位置的值为负无穷，在进行softmax的时候为0)

outputs=[batch_size*h_head,seq_len_q,seq_len_v]

进行sequence mask

构建一个形状为[seq_len_q,seq_len_v]的全1矩阵，将该矩阵转换为一个下三角矩阵(对角线也为1)

将该矩阵扩展为和outputs形状一样的矩阵，记为

future_masks=[batch_size*h_head,seq_len_q,seq_len_v]

构建一个和future_masks形状相同的全1矩阵，并且将它乘以-2 ** 32 + 1

即为paddings=[batch_size*h_head,seq_len_q,seq_len_v]

使用future_masks与0进行比较，如果该位置上为0，则代表该位置需要隐藏，该位置使用padding相应位置的值替换，否则用outputs相应位置上的值代替。

得到最终的结果outputs=[batch_size*h_head,seq_len_q,seq_len_v]

<2.2.3.4>进行softmax

outputs=softmax(outputs)

outputs=[batch_size*h_head,seq_len_q,seq_len_k]

attention=outputs转换形状=[batch_size*h_head,seq_len_k,seq_len_q]

outputs经过dropout

<2.2.3.5>矩阵相乘

outputs=outputs*V=

[batch_size*h_head,seq_len_q,seq_len_k]*[batch_size*h_head,seq_len_v,d_model/h_head]

=[batch_size*h_head,seq_len_q,d_model/h_head]

<2.2.4>进行分割连接

outputs=[batch_size,seq_len_q,d_model]

<2.2.5>进行残差连接

outputs=outputs+Q

<2.2.6>进行归一化

outputs=LayerNormer(outputs)=[batch_size,seq_len_q,d_model]

<2.3>接着计算Multi-Head Attention (encoder-decoder attention)

此时的Q是来自Decoder上一层的输出，K和V是来Encoder的最终输出

Q=outputs=[batch_size,dec_seq_len_q,d_mode],

K=enc_outputs=[batch_size,enc_seq_len_q,d_model]

V=enc_outputs=[batch_size,enc_seq_len_q,d_model]

<2.3.1>首先进行线性运算

Q=Q*[d_model,d_model]=[batch_size,dec_seq_len_q,d_model]

K=Q*[d_model,d_model]=[batch_size,enc_seq_len_q,d_model]

K=Q*[d_model,d_model]=[batch_size,enc_seq_len_q,d_model]

<2.3.2>进行分割

Q=[batch_size*h_head,dec_seq_len_q,d_model/h_head]

K=[batch_size*h_head,enc_seq_len_q,d_model/h_head]

V=[batch_size*h_head,enc_seq_len_q,d_model/h_head]

<2.3.3>计算dot-product attention

<2.3.3.1>矩阵相乘

K改变形状为K=[batch_size*h_head,d_model/h_head,enc_seq_len_q]

outputs=Q*K=[batch_size*h_head,dec_seq_len_q,d_model/h_head]

*[batch_size*h_head,d_model/h_head,enc_seq_len_q]

=[batch_size*h_head,dec_seq_len_q,enc_seq_len_q]

<2.3.3.2>进行scale

d_k=Q.shape[-1]=d_model/h_head

outputs /= d_k ** 0.5

<2.3.3.3>进行padding mask

这里使用的是encoder的mask

src_masks=[batch_size,seq_len] 是一个布尔型的矩阵，如果该位置为空(填充)，值为1

将src_masks扩展成为形状为[batch_size*h_head,seq_len]的矩阵

然后再扩展维度，得到src_masks=[batch_size*h_head,1,seq_len]

将src_masks*负无穷(-2 ** 32 + 1)

outputs=outputs+src_masks(意思是空位置的值为负无穷，在进行softmax的时候为0)

outputs=[batch_size*h_head,dec_seq_len_q,enc_seq_len_q]

<2.3.3.4>进行softmax

outputs=softmax(outputs)

outputs=[batch_size*h_head,dec_seq_len_q,enc_seq_len_q]

attention=outputs转换形状=[batch_size*h_head,enc_seq_len_q,dec_seq_len_q]

outputs经过dropout

<2.3.3.5>矩阵相乘

outputs=outputs*V=

[batch_size*h_head,dec_seq_len_q,enc_seq_len_q]

*[batch_size*h_head,enc_seq_len_q,d_model/h_head]

=[batch_size*h_head,dec_seq_len_q,d_model/h_head]

<2.3.4>进行分割连接

outputs=[batch_size,dec_seq_len_q,d_model]

<2.3.5>进行残差连接

outputs=outputs+Q

<2.3.6>进行归一化

outputs=LayerNormer(outputs)=[batch_size,dec_seq_len_q,d_model]

<2.4>接着计算全连接神经网络

inputs=outputs

outputs=[batch_size,dec_seq_len_q,d_model]*[d_model,d_ff]=[batch_size,dec_seq_len_q,d_ff]

outputs=relu(outputs)

outputs=[batch_size,dec_seq_len_q,d_ff]*[d_ff,d_model]=[batch_size,dec_seq_len_q,d_model]

<2.5>进行残差连接

outputs=outputs+inputs

<2.6>进行归一化

outputs=LayerNormer(outputs)=[batch_size,dec_seq_len_q,d_model]

这样一层的计算就完成了，后面的每一层以outputs为输入继续进行计算

得到最终的结果为outputs=[batch_size,dec_seq_len_q,d_model]

3.关于LOSS的计算

这里我们假设通过encoder得到的最终的输出为

enc_outputs=[batch_size,enc_seq_len_q,d_model]

dec_outputs=[batch_size,dec_seq_len_q,d_model]

通过改变word embedding的形状得到weights=[d_model,vocab_size]

logits=dec_outputs*weights=[batch_size,dec_seq_len_q,vocab_size]

得到结果真实的结果为y_hat=tf.argmax(logits, axis=-1)

这里的y为decoder中不包含但是包含的数据，用来计算损失

y_ = label_smoothing(tf.one_hot(y, depth=vocab_size))

y_=[batch_size,dec_seq_len_q,vocab_size]

ce = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=y_)

ce=[batch_size,dec_seq_len_q]

这里的y为decoder中包含但是不包含的数据

nonpadding = tf.to_float(tf.not_equal(y, 0)) 这里的0为填充字符

nonpadding=[batch_size,dec_seq_len_q]  

loss = tf.reduce_sum(ce * nonpadding) / (tf.reduce_sum(nonpadding) + 1e-7)

如有问题，欢迎指正!!!