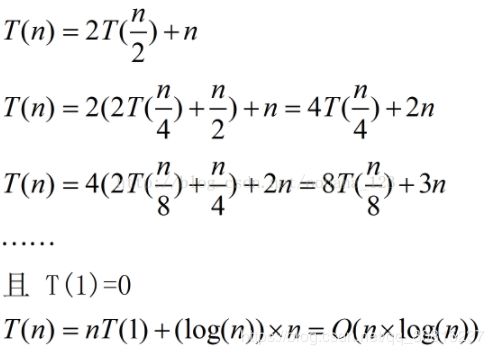各种排序算法的时间复杂度
时间复杂度
当我们评价一个算法的时间性能时，主要标准就是算法的渐近时间复杂度，在算法分析时，经常是将渐近时间复杂度T(n)=O(f(n))简称为时间复杂度，其中的f(n)一般是算法中频度最大的语句频度。算法中语句的频度不仅与问题规模有关，还与输入实例中各元素的取值相关。但是我们总是考虑在最坏的情况下的时间复杂度。以保证算法的运行时间不会比它更长。
常见的时间复杂度，按数量级递增排列依次为：常数阶O(1)、对数阶O(log2n)、线性阶O(n)、线性对数阶O(nlog2n)、平方阶O(n^2)、立方阶O(n^3)、k次方阶O(n^k)、指数阶O(2^n)。常见的算法时间复杂度由小到大依次为：
c < log2N < n < n * Log2N < n^2 < n^3 < 2^n < 3^n < n!
其中c是一个常量，如果一个算法的复杂度为c 、 log2N 、n 、 n*log2N ,那么这个算法时间效率比较高 .
假设运行一行基础代码需要执行一次运算。
int aFunc(void) {
printf("Hello, World!\n"); // 需要执行 1 次
return 0; // 需要执行 1 次
}
那么上面这个方法需要执行 2 次运算
int aFunc(int n) {
for(int i = 0; i这个方法需要 (n + 1 + n + 1) = 2n + 2 次运算。我们把算法需要执行的运算次数用输入大小n的函数表示，即 T(n) ，我们引入时间复杂度的概念。
定义：存在常数 c 和函数 f(n)，使得当 n >= c 时 T(n) <= f(n)，表示为 T(n) = O(f(n)) 。
算法的时间复杂度，用来度量算法的运行时间，记作: T(n) = O(f(n))。它表示随着输入大小n 的增大，算法执行需要的时间的增长速度可以用 f(n) 来描述。
显然如果 T(n) = n^2，那么 T(n) = O(n^2)，T(n) = O(n^3)，T(n) = O(n^4) 都是成立的，但是因为第一个 f(n) 的增长速度与 T(n) 是最接近的，所以第一个是最好的选择，所以我们说这个算法的复杂度是 O(n^2) 。
那么当我们拿到算法的执行次数函数 T(n) 之后怎么得到算法的时间复杂度呢？
常数项对函数的增长速度影响并不大，所以当 T(n) = c，c 为一个常数的时候，我们说这个算法的时间复杂度为 O(1)；如果 T(n) 不等于一个常数项时，直接将常数项省略。
第一个 Hello, World 的例子中 T(n) = 2，所以我们说那个函数(算法)的时间复杂度为 O(1)。
T(n) = n + 29，此时时间复杂度为 O(n)。
高次项对于函数的增长速度的影响是最大的。n^3 的增长速度是远超 n^2 的，同时 n^2 的增长速度是远超 n 的。 同时因为要求的精度不高，所以我们直接忽略低此项。
T(n) = n^3 + n^2 + 29，此时时间复杂度为 O(n^3)。
函数的阶数对函数的增长速度的影响是最显著的，所以我们忽略与最高阶相乘的常数。
T(n) = 3n^3，此时时间复杂度为 O(n^3)。
综合起来：如果一个算法的执行次数是 T(n)，那么只保留最高次项，同时忽略最高项的系数后得到函数 f(n)，此时算法的时间复杂度就是 O(f(n))。由此可见，由执行次数 T(n) 得到时间复杂度并不困难，很多时候困难的是从算法通过分析和数学运算得到 T(n)。对此，提供下列四个便利的法则，这些法则都是可以简单推导出来的，总结出来以便提高效率。
- 对于一个循环，假设循环体的时间复杂度为 O(n)，循环次数为 m，则这个循环的时间复杂度为 O(n×m)。
void aFunc(int n) {
for(int i = 0; i < n; i++) { // 循环次数为 n
printf("Hello, World!\n"); // 循环体时间复杂度为 O(1)
}
}
此时时间复杂度为 O(n × 1)，即 O(n)。
- 对于多个循环，假设循环体的时间复杂度为 O(n)，各个循环的循环次数分别是a, b, c...，则这个循环的时间复杂度为 O(n×a×b×c...)。分析的时候应该由里向外分析这些循环。
void aFunc(int n) {
for(int i = 0; i < n; i++) { // 循环次数为 n
for(int j = 0; j < n; j++) { // 循环次数为 n
printf("Hello, World!\n"); // 循环体时间复杂度为 O(1)
}
}
}
此时时间复杂度为 O(n × n × 1)，即 O(n^2)。
- 对于顺序执行的语句或者算法，总的时间复杂度等于其中最大的时间复杂度。
void aFunc(int n) {
// 第一部分时间复杂度为 O(n^2)
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
printf("Hello, World!\n");
}
}
// 第二部分时间复杂度为 O(n)
for(int j = 0; j < n; j++) {
printf("Hello, World!\n");
}
}
此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。- 对于条件判断语句，总的时间复杂度等于其中时间复杂度最大的路径的时间复杂度。
void aFunc(int n) {
if (n >= 0) {
// 第一条路径时间复杂度为 O(n^2)
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
printf("输入数据大于等于零\n");
}
}
} else {
// 第二条路径时间复杂度为 O(n)
for(int j = 0; j < n; j++) {
printf("输入数据小于零\n");
}
}
}
此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。时间复杂度分析的基本策略是：从内向外分析，从最深层开始分析。如果遇到函数调用，要深入函数进行分析。
求该方法的时间复杂度
void aFunc(int n) {
for (int i = 2; i < n; i++) {
i *= 2;
printf("%i\n", i);
}
}
参考答案：假设循环次数为 t，则循环条件满足 2^t < n。可以得出，执行次数t = log(2)(n)，即 T(n) = log(2)(n)，可见时间复杂度为 O(log(2)(n))，即 O(log n)。
from :https://www.jianshu.com/p/f4cca5ce055a
下面汇总一下创建排序算法的时间复杂度：
冒泡排序：最好的情况是数据本来就有序，复杂度为O(n)；最差的情况是O(
),稳定算法。
选择排序：最好的情况是数据本来就有序，复杂度为O(n)；最差的情况是O(),不稳定算法
直接插入排序：最好的情况是数据本来就有序，复杂度为O(n)；最差的情况是O(),稳定算法
希尔排序：最好的情况复杂度为O(n)；最差的情况是O(),但平均复杂度要比直接插入小，不稳定算法
快速排序：最好的情况复杂度为NlogN,最差的情况是O(),快速排序将不幸退化为冒泡排序;不稳定(比如序列5 3 3 4 3 8 9 10 11，现在中枢元素5和3(第5个元素，下标从1开始计)交换就会把元素3的稳定性打乱)
最优情况:Partition每次都划分得很均匀，如果排序n个关键字，其递归树的深度就为 [log2n]+1（ [x] 表示不大于 x 的最大整数），即仅需递归 log2n 次，需要时间为T（n）的话，第一次Partiation应该是需要对整个数组扫描一遍，做n次比较。然后，获得的枢轴将数组一分为二，那么各自还需要T（n/2）的时间（注意是最好情况，所以平分两半）。于是不断地划分下去，就有了下面的不等式推断：
归并排序：所有情况下都是NlogN，稳定算法。
总时间=分解时间+解决问题时间+合并时间。分解时间就是把一个待排序序列分解成两序列，时间复杂度o(1).解决问题时间是两个递归式，把一个规模为n的问题分成两个规模分别为n/2的子问题，时间为2T(n/2).合并时间复杂度为o（n）。总时间T(n)=2T(n/2)+o(n).这个递归式可以用递归树来解，用递归树的方法解递归式T(n)=2T(n/2)+o(n):假设解决最后的子问题用时为常数c，则对于n个待排序记录来说整个问题的规模为cn。
从这个递归树可以看出，每一层代价都是cn，总共有logn+1层。所以总的时间代价为cn*(logn+1).时间复杂度是o(nlogn)
| 类别 |
排序方法 |
时间复杂度 |
空间复杂度 |
稳定性 |
复杂性 |
特点 |
||
| 最好 |
平均 |
最坏 |
辅助存储 |
|
简单 |
|
||
| 插入 排序 |
直接插入 |
O(N) |
O(N2) |
O(N2) |
O(1) |
稳定 |
简单 |
|
| 希尔排序 |
O(N) |
O(N1.3) |
O(N2) |
O(1) |
不稳定 |
复杂 |
|
|
| 选择 排序 |
直接选择 |
O(N) |
O(N2) |
O(N2) |
O(1) |
不稳定 |
|
|
| 堆排序 |
O(N*log2N) |
O(N*log2N) |
O(N*log2N) |
O(1) |
不稳定 |
复杂 |
|
|
| 交换 排序 |
冒泡排序 |
O(N) |
O(N2) |
O(N2) |
O(1) |
稳定 |
简单 |
1、冒泡排序是一种用时间换空间的排序方法 |
| 快速排序 |
O(N*log2N) |
O(N*log2N) |
O(N2) |
O(log2n)~O(n) |
不稳定 |
复杂 |
1、n大时好，快速排序比较占用内存，内存随n的增大而增大，但却是效率高不稳定的排序算法。 |
|
| 归并排序 |
O(N*log2N) |
O(N*log2N) |
O(N*log2N) |
O(n) |
稳定 |
复杂 |
1、n大时好，归并比较占用内存，内存随n的增大而增大，但却是效率高且稳定的排序算法。 |
|
| 基数排序 |
O(d(r+n)) |
O(d(r+n)) |
O(d(r+n)) |
O(rd+n) |
稳定 |
复杂 |
|
|
| 注：r代表关键字基数，d代表长度，n代表关键字个数，“2”是底数， |
||||||||
from：https://www.cnblogs.com/xiaochun126/p/5086037.html