LS-GAN（损失敏感GAN）

PS: 获取更好的阅读体验，请前往知乎专栏。

　　好早以前就说要写一篇LS-GAN，loss sensitive GAN[1]的读书笔记，一直没有写，今天就来聊聊LS-GAN，请注意，它不是我们上一期所说的LSGAN（least square GAN）。

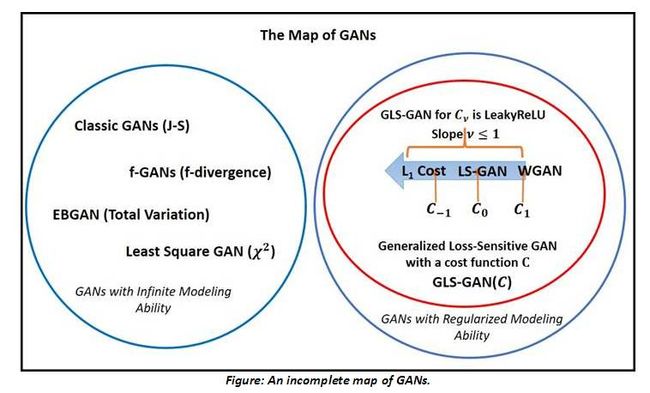
　　开始本期文章解读之前，先来回答以下上上期谈LSGAN时留下的问题，当时提到了least square GAN优化的目标是Pearson 散度，属于f-divergence的一种，然后提到了其他的divergence是否也能用到GAN的训练中，当时没推导出来，后来发现有一篇文章[4]将所有的f-divergence对应的GAN的形式都推导出来了，参见下图。

　　

　　值得一提的是，作者刘国君老师也在知乎专栏介绍了LS-GAN，他写的更专业严谨一些，感兴趣的童靴可以移步：

　　条条大路通罗马LS-GAN：把GAN建立在Lipschitz密度上 - 知乎专栏

　　广义LS-GAN（GLS-GAN):现在 LS-GAN和WGAN都是这个超模型的特例了 - 知乎专栏

　　

（图片来源于[3]）

　　下面，我会用与上面两篇文章不同的视角（类比SVM）来解读LS-GAN，这个视角是GAN讨论群里面有个童鞋提出来的。

　　在了解LS-GAN之前，我们先来回顾一下SVM，后面你会看到，两者有相似的地方。

　　SVM

　　假定我们有一批数据，它是线性可分的。通常来说，我们可以通过求解下面的优化问题来得到一个线性SVM分类器：

　　也就是说，在保证每个样本点与超平面的几何间隔至少为的情况下，我们尽可能地最大化这个间隔。

　　当数据线性不可分的时候，我们可以不必要求每个样本点都满足几何间隔至少为的要求（因为那样将导致问题不可解），通过引入一个松弛变量来放宽约束条件

　　上式虽然允许有误分类的样本点，但是它要求误分类尽可能地少。

　　LS-GAN

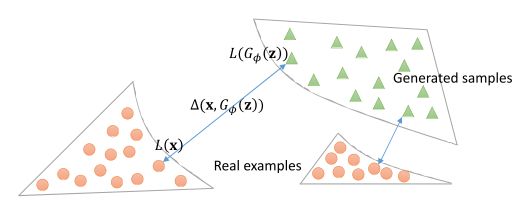
　　我们知道GAN分为generator（G）和discriminator（D），D实际上是一个分类器，用于分类输入图像是真实图像还是G产生的图像。这里说的误分类点就是D错误分类的数据。对于任意一组数据，我们可以根据D的输出定义它的loss为，为损失函数。对GAN来说，fake数据来自于G，我们可以简化符号，将D嵌入到loss中，记为真实数据（real），而G生成的数据为fake，这样，对应的loss分别可以简化写成和，其中为D的参数。

　　从优化的角度来看，real数据的loss应该比fake数据的loss来得小，小多少呢？跟两者的相似度有关，写成约束条件就是

　　是相似性度量，可以自定义，一般来说用p范数就行了。

　　这跟上面提到的线性可分情形下的SVM有相似之处。不过，SVM要求所有的margin至少为，而这里采用的margin与数据间的相似性有关（是不是采用相同的margin也可以？可以尝试，采用与数据相似性相关的margin可以让GAN专注于那些生成质量较差的数据，也就是“按需分配”[2]）。

　　随着G学得越来越好，会越来越小，D越来越难区分real和fake的数据（当然，这也是我们的目标），上述的约束条件可以会无法满足，训练可能会出现震荡，陷入僵局。

　　类似于SVM，当数据不可分时，可以引入松弛变量，于是约束条件可以改写成

　　这样，固定G，我们可以通过下面的优化问题求解D：

　　进一步地，将约束条件放到目标函数上去，可以改写为

　　这里，称为函数的正部，为了方便，下面称它为正部函数。对于正部函数，当时，，否则。

　　而对于G，固定D（也就是固定），我们可以通过如下规划优化G：

　　在实际训练中，这两个优化问题交替求解，而且无需求解到最优再转向另一个问题，通常来说，每次迭代，D更新步，G更新一步。

　　作者在[1]中证明了，若真实数据分布的支撑集为紧致集，并且是Lipschitz连续的，则当时，LS-GAN将收敛到纳什均衡解，。这也启示我们，在实际训练时，应该设置为一个较大的数。

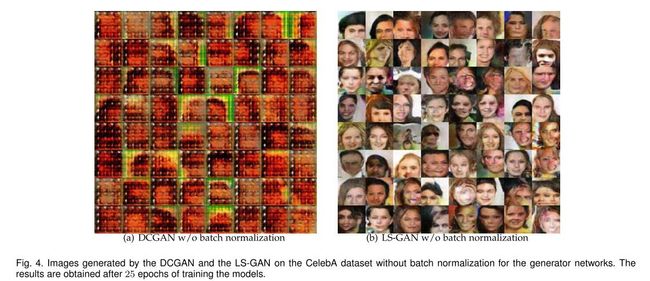
　　作者通过实验验证了LS-GAN的有效性，并且发现，即使不使用batch normalization，LS-GAN仍然能够产生decent的图像。

　　CLS-GAN

　　不难理解，带条件的LS-GAN的loss可以记为，其中为条件信息。对应的优化问题分别为：

　　同样地，与其他GAN的conditional版本一样，它也可以做预测问题：

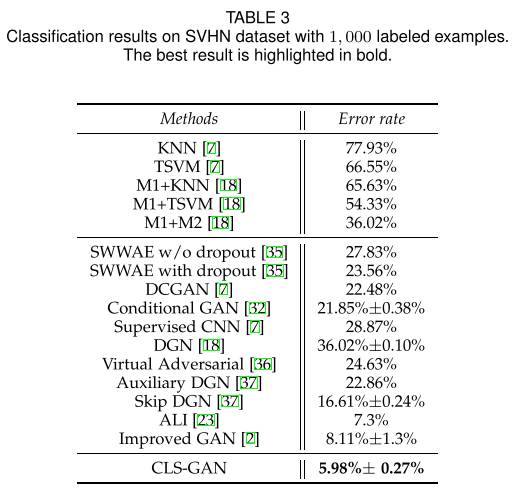
　　作者在SVHN数据集上测试了预测问题（监督学习），CLS-GAN取得了不错的分类结果：

　　LS-GAN做半监督学习

　　设我们的数据包含个类别。我们知道，general GAN做半监督学习，一般是将G产生的数据当做单独的一类数据，而真实的类数据一起构成类的数据，D的任务是正确分类这类的数据（参看Improved GAN）。

　　当计算loss时，还是按照real和fake两类进行计算，即真实的类数据算为real，而G产生的数据，即第类数据算为fake。采用JS散度即可定义loss。一般来说，没有标签的数据只来自于G。

　　当然，LS-GAN也可以这么做。作者采用另外一种方式，从CLS-GAN入手做半监督学习。

　　首先，由于是分类问题，loss可以根据softmax的输出来定义

　　对于没有标签的数据（与Improved GAN中所用的方法不同，这里不只是G产生的数据，还可以没有标签的真实数据），它的标签可以通过CLS-GAN进行预测，对应的，这类数据的loss可以定义为

　　对有标签和没有标签的数据做一个平衡（设平衡参数为），可以得到最终的目标函数：

　　其中：

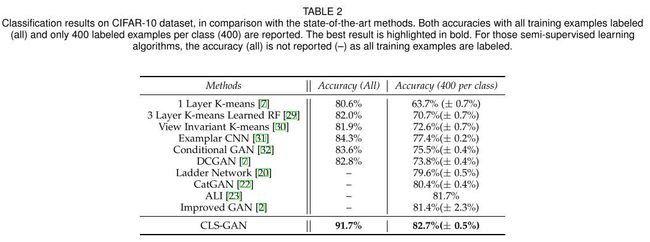
　　实验发现，CLS-GAN在CIFAR数据集上的半监督学习达到了state-of-the-art的水平。

　　GLS-GAN

　　最后，作者对LS-GAN做了一个推广，得到广义的LS-GAN，GLS-GAN。

　　回顾一下，前面LS-GAN引入了非负的松弛变量，并最终将松弛变量合并到目标函数中（通过正部函数）。这个过程只用到了正部函数的两个性质：

　　1.

　　2.

　　我们可以用一个满足这两个性质的其他函数来代替正部函数，比如leaky relu函数。记为满足以上两个性质的函数，它可以用于替换正部函数：

　　当足够大时，我们可以忽略第一项：

　　若采用leaky relu函数，此时的GLS-GAN记为，不难看出

　　而当时，与无关，可以忽略，此时D的目标函数为：

　　而这就是WGAN的目标函数！也就是说

　　也就是说，LS-GAN和WGAN都是GLS-GAN的特例。

　　此外，可以尝试其他类型的C函数，个人觉得，换成其他类型的C函数，对效果的影响并不大。文章的结果我还没复现，待复现结果时验证一下。

　　代码

　　1. LS-GAN： https://github.com/guojunq/lsgan

　　2. GLS-GAN: https://github.com/guojunq/glsgan

　　参考文献

　　1. Qi G J. Loss-Sensitive GenerativeAdversarial Networks on Lipschitz Densities[J]. arXiv preprintarXiv:1701.06264, 2017.

　　2. 知乎专栏：条条大路通罗马LS-GAN：把GAN建立在Lipschitz密度上 - 知乎专栏

　　3. An Incomplete Map of the GAN models: http://www.cs.ucf.edu/~gqi/GANs.htm

　　4. Nowozin S, Cseke B, Tomioka R. f-GAN:Training generative neural samplers using variational divergenceminimization[C]//Advances in Neural Information Processing Systems. 2016:271-279.