B+树的Java实现(B+ Tree)
B+树 B+ Tree
定义
B+树是一种多路平衡查找树,是对B树(B-Tree)的扩展.
首先,一个M阶的B树的定义为:
- 每个节点最多有M个子节点;
- 每一个非叶子节点(除根节点)至少有ceil(M/2)个子节点;
- 如果根节点不是叶子节点,那么至少有两个子节点;
- 有k个子节点的非叶子节点拥有k-1个键,键按照升序排列;
- 所有叶子节点在同一层;
从定义可以看出来,一个M阶的B树,其叶子节点必须在同一层,每一个节点的子节点数目和键数目都是有规定的.其实不看定义,简单来说,B树是平衡的,而且非叶子节点的子节点是有限制的.最重要的一点是,B树的键是有序的,节点内部的键从左到右依次增大,而且对应的子节点的最小值和最大值在左右两个键之间,这样可以尽可能减少IO次数,提高查询效率.
而B+树基本定义与B树相同,不同之处在于:
- 非叶节点仅有索引作用,具体信息均存放在叶节点;
- 树的所有叶子节点构成一个有序链表,可以按照键的排序次序遍历全部记录;
其实理解起来也不难,就是所以非叶子节点只存储索引,不存储真正的值,而父节点所拥有的边界值在子节点中都存在.
我的理解是,虽然B+树相较于平衡二叉树实现麻烦,结构复杂,插入麻烦,但是M阶的B树,M越大,最后的树就越”粗壮”,查询所需要的次数也就越少,因为在数据库数据非常多时,索引文件无法全部加载到内存,而进行磁盘IO是非常耗时的,当然是越少越好.所以虽然B+树和平衡二叉树的查询时间复杂度差不多,但是B+树相较于平衡二叉树更适合实现数据库的索引.
例子
建立一个阶为4的B+树,随机一些数据进行插入(只用key,忽略value):
10,17,3,29,6,5,18,4,22,1,33,35
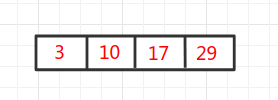
首先,依次插入10,17,3,19,都能存放在初始节点中,在插入时会查找到正确的位置并且进行插入:
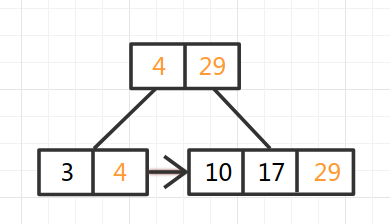
之后插入6,插入成功后发现当前节点的键的数量为5,大于了最大值4,所以需要从中间拆分为两部分,同时把拆分后的两个节点最大的键取出来插入到父节点中(图中橙色节点):
之后继续插入5,18,4都能够成功插入.5插入时先从根节点出发,因为小于第一个key 6,所直接插入6对应的子节点。18插入时因为大于6小于29,所以插入到29对应的子节点。(如果插入的数大于29,同样会插入到29对应的子节点,但是同时会更新非叶子结点的值,保证非叶子结点键始终是它所指向的子节点的最大值。)插入的结果应该为
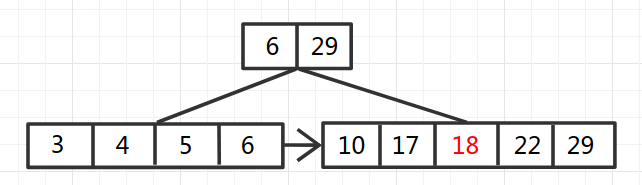
之后插入22,因为22大于6小于29,所以插入29对应叶子节点。插入后叶子节点超过上限,进行拆分,拆分后仍然将拆分的两部分的最大值插入到父节点:
之后按照此规则继续插入1,1小于6,则直接插入到6对应叶子节点,这个4阶B树将变成:
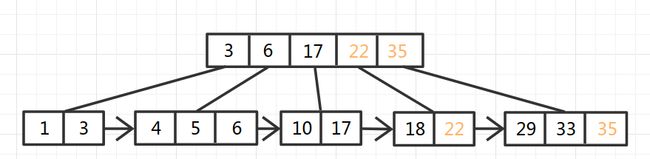
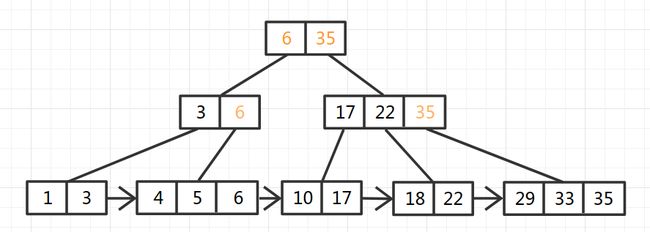
再拆入33,35,注意,插入33时,因为33大于了最大值29,所以需要更新父节点的最大值,这样才能保证父节点键值始终是其指向的节点的最大值。插入35时,叶节点分解成两个,然后依旧将分解之后的结果发送到父节点,父节点更新节点和指针,更新后发现当前节点也超过了4个,那么当前节点也进行分解,生成父节点,如此重复,直到没有节点为止:
图中没有画出的一点是,所有的值都只在叶子节点存储,非叶子节点只有键,不存储值.
查询时则十分简单,非叶子节点直接顺序比较,找到区间则递归调用查找函数,叶子节点则采用二分查找,找到对应节点.
实现
类型
原理大概搞懂之后,可以考虑开始实现了。
首先考虑的问题是数据类型,用来作为B+树索引的键的肯定是某个拥有很多个属性的对象,那么数据类型应该使用泛型,这个应该没有太大问题。
之后需要考虑的问题就是,类的排序规则。因为在B+树的实现过程中,需要比较不同键的大小,那么泛型类来说就需要能够比较大小,那就意味着必须是comparable的子类。用extends Comparable可以指定泛型上限,可以解决这个问题。
节点
类型确定用泛型之后,接下来应该思考B+树实现应该有哪些类,按照写二叉树的经验,首先考虑到的就是节点类。
实现节点类是要结合上面的定义来考虑节点类应该有哪些,首先每个节点应该有一系列的键,键的数量取决于多种因素,那么最好采用数组。其实还应该有指向父节点和子节点的指针,其中父节点只需要有一个,而子节点有多个,同样需要采用数组。最好还有一个变量来方便得记录子节点和键的数量,这样获取节点数量时比较方便,节点的属性大概就是这么多了。
在确定了节点的属性之后,要考虑节点类会有哪些方法,首先构造方法肯定需要有的,在构造方法中完成相关属性的初始化。
节点分为叶节点和非叶节点,叶节点需要额外存储数据,所以数据结构不太一样,非叶节点也有自己的查询和插入逻辑,所以应该把节点类作为抽象类,叶节点和非叶节点都继承这个类。
非叶节点的查询是遍历整个数组,找到对应的子节点然后进行递归查询,具体对应方法可以参考下面的例子。非叶节点的插入同样也是找到应该插入的子树进递归插入。
叶节点需要专门定义一个数组用来存储键对应的值,还需要实现具体的查询和插入方法。查询可以顺序查询,这里采用二分搜索来节约点时间。插入就比较复杂了,因为插入叶节点时需要保证整个B+树的平衡。
叶节点进行插入时,首先找到数组里面应该插入的数据的正确位置,然后把数组挪一挪把数据放进来。挪数组这个实现虽然麻烦但是原理简单,就不详细说了。挪完数组后,就需要判断数据数量是否超过上限了,如果超过上限,则需要对当前节点进行分裂,我的做法是一半一半,奇数时左边比右边少一个数据,偶数时都一样。分裂成两个节点并且完成数据复制后,还没有结束,需要把新产生的节点插入父节点,所以非叶节点需要有一个方法来处理这种情况。因为插入父节点的同时还需要更新子节点指针,所以干脆把两个节点作为参数传过去。同时,父节点键也有很多,为了精准地进行插入,我们还需要传入旧键来弄清楚插入的两个节点应该放到哪里。
父节点的插入方法拿到了旧键和需要插入的两个节点,那么首先根据旧键找到了应该插入的位置,然后新的两个键取代旧的一个键,新的两个指针取代旧的指针,又是疯狂地挪位置。完成插入之后,和叶节点的插入类似,也需要判断是否超出上限了,如果超出了上限那么同样需要进行拆分,拆分也和子节点拆分类似,拆完了递归调用自身,这样就能够保证B+树始终是平衡的。
当然,上面只是说大概过程,具体实现时还有很多细节和小问题,可以看我代码里的注释来看一下我是怎么做的。
代码
BPlusTree.java
package bPlusTree;
/**
* 实现B+树
*
* @param 指定值类型
* @param 使用泛型,指定索引类型,并且指定必须继承Comparable
*/
public class BPlusTree <T, V extends Comparable<V>>{
//B+树的阶
private Integer bTreeOrder;
//B+树的非叶子节点最小拥有的子节点数量(同时也是键的最小数量)
//private Integer minNUmber;
//B+树的非叶子节点最大拥有的节点数量(同时也是键的最大数量)
private Integer maxNumber;
private Node<T, V> root;
private LeafNode<T, V> left;
//无参构造方法,默认阶为3
public BPlusTree(){
this(3);
}
//有参构造方法,可以设定B+树的阶
public BPlusTree(Integer bTreeOrder){
this.bTreeOrder = bTreeOrder;
//this.minNUmber = (int) Math.ceil(1.0 * bTreeOrder / 2.0);
//因为插入节点过程中可能出现超过上限的情况,所以这里要加1
this.maxNumber = bTreeOrder + 1;
this.root = new LeafNode<T, V>();
this.left = null;
}
//查询
public T find(V key){
T t = this.root.find(key);
if(t == null){
System.out.println("不存在");
}
return t;
}
//插入
public void insert(T value, V key){
if(key == null)
return;
Node<T, V> t = this.root.insert(value, key);
if(t != null)
this.root = t;
this.left = (LeafNode<T, V>)this.root.refreshLeft();
// System.out.println("插入完成,当前根节点为:");
// for(int j = 0; j < this.root.number; j++) {
// System.out.print((V) this.root.keys[j] + " ");
// }
// System.out.println();
}
/**
* 节点父类,因为在B+树中,非叶子节点不用存储具体的数据,只需要把索引作为键就可以了
* 所以叶子节点和非叶子节点的类不太一样,但是又会公用一些方法,所以用Node类作为父类,
* 而且因为要互相调用一些公有方法,所以使用抽象类
*
* @param 同BPlusTree
* @param
*/
abstract class Node<T, V extends Comparable<V>>{
//父节点
protected Node<T, V> parent;
//子节点
protected Node<T, V>[] childs;
//键(子节点)数量
protected Integer number;
//键
protected Object keys[];
//构造方法
public Node(){
this.keys = new Object[maxNumber];
this.childs = new Node[maxNumber];
this.number = 0;
this.parent = null;
}
//查找
abstract T find(V key);
//插入
abstract Node<T, V> insert(T value, V key);
abstract LeafNode<T, V> refreshLeft();
}
/**
* 非叶节点类
* @param
* @param
*/
class BPlusNode <T, V extends Comparable<V>> extends Node<T, V>{
public BPlusNode() {
super();
}
/**
* 递归查找,这里只是为了确定值究竟在哪一块,真正的查找到叶子节点才会查
* @param key
* @return
*/
@Override
T find(V key) {
int i = 0;
while(i < this.number){
if(key.compareTo((V) this.keys[i]) <= 0)
break;
i++;
}
if(this.number == i)
return null;
return this.childs[i].find(key);
}
/**
* 递归插入,先把值插入到对应的叶子节点,最终讲调用叶子节点的插入类
* @param value
* @param key
*/
@Override
Node<T, V> insert(T value, V key) {
int i = 0;
while(i < this.number){
if(key.compareTo((V) this.keys[i]) < 0)
break;
i++;
}
if(key.compareTo((V) this.keys[this.number - 1]) >= 0) {
i--;
// if(this.childs[i].number + 1 <= bTreeOrder) {
// this.keys[this.number - 1] = key;
// }
}
// System.out.println("非叶子节点查找key: " + this.keys[i]);
return this.childs[i].insert(value, key);
}
@Override
LeafNode<T, V> refreshLeft() {
return this.childs[0].refreshLeft();
}
/**
* 当叶子节点插入成功完成分解时,递归地向父节点插入新的节点以保持平衡
* @param node1
* @param node2
* @param key
*/
Node<T, V> insertNode(Node<T, V> node1, Node<T, V> node2, V key){
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1]);
V oldKey = null;
if(this.number > 0)
oldKey = (V) this.keys[this.number - 1];
//如果原有key为null,说明这个非节点是空的,直接放入两个节点即可
if(key == null || this.number <= 0){
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + "直接插入");
this.keys[0] = node1.keys[node1.number - 1];
this.keys[1] = node2.keys[node2.number - 1];
this.childs[0] = node1;
this.childs[1] = node2;
this.number += 2;
return this;
}
//原有节点不为空,则应该先寻找原有节点的位置,然后将新的节点插入到原有节点中
int i = 0;
while(key.compareTo((V)this.keys[i]) != 0){
i++;
}
//左边节点的最大值可以直接插入,右边的要挪一挪再进行插入
this.keys[i] = node1.keys[node1.number - 1];
this.childs[i] = node1;
Object tempKeys[] = new Object[maxNumber];
Object tempChilds[] = new Node[maxNumber];
System.arraycopy(this.keys, 0, tempKeys, 0, i + 1);
System.arraycopy(this.childs, 0, tempChilds, 0, i + 1);
System.arraycopy(this.keys, i + 1, tempKeys, i + 2, this.number - i - 1);
System.arraycopy(this.childs, i + 1, tempChilds, i + 2, this.number - i - 1);
tempKeys[i + 1] = node2.keys[node2.number - 1];
tempChilds[i + 1] = node2;
this.number++;
//判断是否需要拆分
//如果不需要拆分,把数组复制回去,直接返回
if(this.number <= bTreeOrder){
System.arraycopy(tempKeys, 0, this.keys, 0, this.number);
System.arraycopy(tempChilds, 0, this.childs, 0, this.number);
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + ", 不需要拆分");
return null;
}
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + ",需要拆分");
//如果需要拆分,和拆叶子节点时类似,从中间拆开
Integer middle = this.number / 2;
//新建非叶子节点,作为拆分的右半部分
BPlusNode<T, V> tempNode = new BPlusNode<T, V>();
//非叶节点拆分后应该将其子节点的父节点指针更新为正确的指针
tempNode.number = this.number - middle;
tempNode.parent = this.parent;
//如果父节点为空,则新建一个非叶子节点作为父节点,并且让拆分成功的两个非叶子节点的指针指向父节点
if(this.parent == null) {
// System.out.println("非叶子节点,插入key: " + node1.keys[node1.number - 1] + " " + node2.keys[node2.number - 1] + ",新建父节点");
BPlusNode<T, V> tempBPlusNode = new BPlusNode<>();
tempNode.parent = tempBPlusNode;
this.parent = tempBPlusNode;
oldKey = null;
}
System.arraycopy(tempKeys, middle, tempNode.keys, 0, tempNode.number);
System.arraycopy(tempChilds, middle, tempNode.childs, 0, tempNode.number);
for(int j = 0; j < tempNode.number; j++){
tempNode.childs[j].parent = tempNode;
}
//让原有非叶子节点作为左边节点
this.number = middle;
this.keys = new Object[maxNumber];
this.childs = new Node[maxNumber];
System.arraycopy(tempKeys, 0, this.keys, 0, middle);
System.arraycopy(tempChilds, 0, this.childs, 0, middle);
//叶子节点拆分成功后,需要把新生成的节点插入父节点
BPlusNode<T, V> parentNode = (BPlusNode<T, V>)this.parent;
return parentNode.insertNode(this, tempNode, oldKey);
}
}
/**
* 叶节点类
* @param
* @param
*/
class LeafNode <T, V extends Comparable<V>> extends Node<T, V> {
protected Object values[];
protected LeafNode left;
protected LeafNode right;
public LeafNode(){
super();
this.values = new Object[maxNumber];
this.left = null;
this.right = null;
}
/**
* 进行查找,经典二分查找,不多加注释
* @param key
* @return
*/
@Override
T find(V key) {
if(this.number <=0)
return null;
// System.out.println("叶子节点查找");
Integer left = 0;
Integer right = this.number;
Integer middle = (left + right) / 2;
while(left < right){
V middleKey = (V) this.keys[middle];
if(key.compareTo(middleKey) == 0)
return (T) this.values[middle];
else if(key.compareTo(middleKey) < 0)
right = middle;
else
left = middle;
middle = (left + right) / 2;
}
return null;
}
/**
*
* @param value
* @param key
*/
@Override
Node<T, V> insert(T value, V key) {
// System.out.println("叶子节点,插入key: " + key);
//保存原始存在父节点的key值
V oldKey = null;
if(this.number > 0)
oldKey = (V) this.keys[this.number - 1];
//先插入数据
int i = 0;
while(i < this.number){
if(key.compareTo((V) this.keys[i]) < 0)
break;
i++;
}
//复制数组,完成添加
Object tempKeys[] = new Object[maxNumber];
Object tempValues[] = new Object[maxNumber];
System.arraycopy(this.keys, 0, tempKeys, 0, i);
System.arraycopy(this.values, 0, tempValues, 0, i);
System.arraycopy(this.keys, i, tempKeys, i + 1, this.number - i);
System.arraycopy(this.values, i, tempValues, i + 1, this.number - i);
tempKeys[i] = key;
tempValues[i] = value;
this.number++;
// System.out.println("插入完成,当前节点key为:");
// for(int j = 0; j < this.number; j++)
// System.out.print(tempKeys[j] + " ");
// System.out.println();
//判断是否需要拆分
//如果不需要拆分完成复制后直接返回
if(this.number <= bTreeOrder){
System.arraycopy(tempKeys, 0, this.keys, 0, this.number);
System.arraycopy(tempValues, 0, this.values, 0, this.number);
//有可能虽然没有节点分裂,但是实际上插入的值大于了原来的最大值,所以所有父节点的边界值都要进行更新
Node node = this;
while (node.parent != null){
V tempkey = (V)node.keys[node.number - 1];
if(tempkey.compareTo((V)node.parent.keys[node.parent.number - 1]) > 0){
node.parent.keys[node.parent.number - 1] = tempkey;
node = node.parent;
}
else {
break;
}
}
// System.out.println("叶子节点,插入key: " + key + ",不需要拆分");
return null;
}
// System.out.println("叶子节点,插入key: " + key + ",需要拆分");
//如果需要拆分,则从中间把节点拆分差不多的两部分
Integer middle = this.number / 2;
//新建叶子节点,作为拆分的右半部分
LeafNode<T, V> tempNode = new LeafNode<T, V>();
tempNode.number = this.number - middle;
tempNode.parent = this.parent;
//如果父节点为空,则新建一个非叶子节点作为父节点,并且让拆分成功的两个叶子节点的指针指向父节点
if(this.parent == null) {
// System.out.println("叶子节点,插入key: " + key + ",父节点为空 新建父节点");
BPlusNode<T, V> tempBPlusNode = new BPlusNode<>();
tempNode.parent = tempBPlusNode;
this.parent = tempBPlusNode;
oldKey = null;
}
System.arraycopy(tempKeys, middle, tempNode.keys, 0, tempNode.number);
System.arraycopy(tempValues, middle, tempNode.values, 0, tempNode.number);
//让原有叶子节点作为拆分的左半部分
this.number = middle;
this.keys = new Object[maxNumber];
this.values = new Object[maxNumber];
System.arraycopy(tempKeys, 0, this.keys, 0, middle);
System.arraycopy(tempValues, 0, this.values, 0, middle);
this.right = tempNode;
tempNode.left = this;
//叶子节点拆分成功后,需要把新生成的节点插入父节点
BPlusNode<T, V> parentNode = (BPlusNode<T, V>)this.parent;
return parentNode.insertNode(this, tempNode, oldKey);
}
@Override
LeafNode<T, V> refreshLeft() {
if(this.number <= 0)
return null;
return this;
}
}
}
以下代码用于测试:
Product.java
package bPlusTree;
public class Product {
private Integer id;
private String name;
private Double price;
public Product(Integer id, String name, Double price) {
this.id = id;
this.name = name;
this.price = price;
}
public Integer getId() {
return id;
}
public void setId(Integer id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Double getPrice() {
return price;
}
public void setPrice(Double price) {
this.price = price;
}
}
Test.java
package bPlusTree;
public class Test {
public static void main(String[] args){
BPlusTree<Product, Integer> b = new BPlusTree<>(4);
long time1 = System.nanoTime();
for (int i = 0; i < 10000; i++) {
Product p = new Product(i, "test", 1.0 * i);
b.insert(p, p.getId());
}
long time2 = System.nanoTime();
Product p1 = b.find(345);
long time3 = System.nanoTime();
System.out.println("插入耗时: " + (time2 - time1));
System.out.println("查询耗时: " + (time3 - time2));
}
}
参考内容
- B树和B+树:https://www.cnblogs.com/vincently/p/4526560.html
- wiki百科 B树: https://zh.wikipedia.org/wiki/B树
- B+树的实现: https://blog.csdn.net/TVXQ_xy/article/details/53006561