BP算法实现--minst手写数字数据集识别

实验步骤

初始化网络架构

网络层数，每层神经元数，连接神经元的突触权重，每个神经元的偏置

构造bp算法函数

1. 对于一个输入数据，前向计算每层的输出值，保存未激活的输出和激活过的输出值，这里用的激活函数是sigmoid
2. 根据最后一层的输出值计算出相应的δ，再依次反向计算对应层的δ。
3. 根据得到的δ，可以得到每层的Δw和Δb。
4. 更新网络中w , b
   遍历训练集中的每个训练样本，每个样本通过bp算法所得到的Δw和Δb各自累加，最后通过
   $w-sum(\Delta w)\ast \eta /len(trainin{g}_{s}et)$ 计算出更新后的w和b。
5. 使用SGD（随机梯度下降）来优化网络，减少模型损失
   将训练集分成若干个小的训练集，每个训练集使用更新函数来更新网络中的w,b的值。设置一个迭代次数值epochs,每次迭代首先打乱训练集，将上述过程重复epochs次。
6. 预测程序运行结果
   对于每次迭代得到的w和b的值，使用测试集中的每个数据前向计算输出，得到预测正确的数据数。依次输出每次迭代后的预测正确数。

数据集描述

这里的数据集使用的是MINST数据集，是由Yann提供的手写数字数据集文件，这个数据集主要包含了50000个的训练数据和10000个的测试数据。每个数据导入成（x,y）的元组，x是28*28的图片，这里是784维的向量，y是对应的数字标签。

测试结果

由于数据集的输入是784维，输出是10维的数据，所以选择的网络架构为【784 30 10】.学习率η为3.0，迭代次数为30.输出的10维向量每一位对应着该数字的得分，哪一维的得分最高即该数据的预测结果。每次迭代后将更新后的网络计算测试集的数据，统计预测正确的个数。实验结果如下图所示：

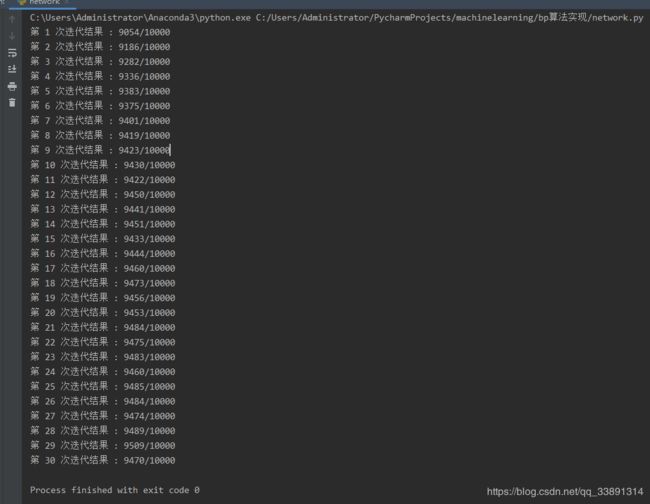
从该实验结果可以看出，尽管正确率在某些迭代次数中小有下跌，这是因为在某些迭代过程中初始点选择导致的。但是总体上的趋势随着迭代次数的增加，手写数字预测的正确率逐渐提高。

源代码

神经网络部分代码

import numpy as np
import mnist_loader


class Network:
    def __init__(self, size):
        # 网络的架构：层数 每层的神经元
        self.num_layers = len(size)
        self.size = size
        # 除第一层外神经元的偏置和连接神经元突触的权值
        self.biases = [np.random.randn(n, 1) for n in size[1:]]  # 偏置
        self.weights = [np.random.randn(m, n) for n, m in zip(size[: -1], size[1:])]  # 权值

    # 激活函数
    def sigmoid(self, x):
        return 1.0/(1.0 + np.exp(-x))

    # 激活函数sigmoid的导数
    def derivative_sigmoid(self, x):
        return self.sigmoid(x) * (1-self.sigmoid(x))

    def backpropagation(self, x, y):
        # 初始化Δb 和 Δw
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # 前向计算
        a = x  # 每层的输出
        a_s = [x]  # 保存每层的输出向量
        v_s = []  # 保存每层未激活的输出向量
        for w, b in zip(self.weights, self.biases):
            v = np.dot(w, a) + b
            v_s.append(v)
            a = self.sigmoid(v)
            a_s.append(a)

        # 计算最后一层的δ
        delta = (a_s[-1] - y) * self.derivative_sigmoid(v_s[-1])
        # 计算最后一层的Δb 和 Δw
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, a_s[-2].T)
        # 依次向前计算每层的δ和相应的Δb 和 Δw
        for i in range(2, self.num_layers):
            v = v_s[-i]
            delta = np.dot(self.weights[-i+1].T, delta) * self.derivative_sigmoid(v)
            nabla_b[-i] = delta
            nabla_w[-i] = np.dot(delta, a_s[-i-1].T)
        return nabla_b, nabla_w

    # 根据数据集来更新w和b的值
    def update(self, data_set, eta):
        # 对于整个数据集的Δb和Δw
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # 累加每个样本的Δb和Δw
        for x, y in data_set:
            i_nabla_b, i_nabla_w = self.backpropagation(x, y)
            nabla_b = [inb+nb for inb, nb in zip(i_nabla_b, nabla_b)]
            nabla_w = [inw+nw for inw, nw in zip(i_nabla_w, nabla_w)]
        # 更新w,b的值
        self.biases = [b - (eta/len(data_set))*nb for b, nb in zip(self.biases, nabla_b)]
        self.weights = [w - (eta/len(data_set))*nw for w, nw in zip(self.weights, nabla_w)]

    # 前行计算数据的输出
    def feedforward(self, x):
        for b, w in zip(self.biases, self.weights):
            x = self.sigmoid(np.dot(w, x)+b)
        return x

    def evaluate(self, test_data):
        # 获得预测结果
        test_results = []
        a = np.zeros([784, 1])
        for (x, y) in test_data:
            test_results.append((np.argmax(self.feedforward(x)), y))
        # 返回正确识别的个数
        return sum(int(x == y) for (x, y) in test_results)

    def SGD(self, training_set, epochs, mini_batch_size, eta, test_set=None):
        if test_set:
            num_test = len(test_set)  # 测试集的长度
        n = len(training_set)  # 训练集的长度
        for i in range(1, epochs+1):  # 迭代遍历
            np.random.shuffle(training_set)  # 打乱训练集
            # 划分训练集
            mini_batches = [training_set[k:k+mini_batch_size]
                            for k in range(0, n, mini_batch_size)]
            # 对每个训练集更新网络数据
            for mini_batch in mini_batches:
                self.update(mini_batch, eta)
            if test_set:
                print("第 {0} 次迭代结果 : {1}/{2}".format(i, self.evaluate(test_set), num_test))
            else:
                print("迭代 {0} 次完成".format(i-1))


training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
net = Network([784, 30, 10])
net.SGD(training_data, 30, 10, 3.0, test_data)

导入数据集部分代码

import pickle
import gzip
import numpy as np


def load_data():
    f = gzip.open('mnist.pkl.gz', 'rb')
    training_data, validation_data, test_data = pickle.load(f, encoding="bytes")
    f.close()
    return training_data, validation_data, test_data


def load_data_wrapper():
    tr_d, va_d, te_d = load_data()
    training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
    training_results = [vectorized_result(y) for y in tr_d[1]]
    training_data = zip(training_inputs, training_results)
    validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
    validation_data = zip(validation_inputs, va_d[1])
    test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
    test_data = zip(test_inputs, te_d[1])
    return list(training_data), list(validation_data), list(test_data)


def vectorized_result(j):
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e

问题回顾

在本次实验中被一个问题困扰好几天，刚开始实验结果每次迭代结果都是一模一样，识别成功要么都是九百多或者一千出头。

我首先想到的是BP算法或者在梯度下降哪里出了问题导致网络一直没有更新，所以输出了每次迭代的w和b的值，发现都进行了更新。

然后我输出每次的预测结果 test_results，这里保存每个测试数据预测之后的样本值和相应的标签，发现在一次迭代中所有样本的预测值都是一样的。到这里我开始怀疑是不是数据集出了问题，然后我检查测试集的样本数据，发现样本都是不一样的。

这样问题就很诡异了，一次迭代中同样的网络，同样的参数，10000个不同的样本却都有着相同的输出，百思不得其解。然后就开始各种百度各种教程，都没有合理的解释，直到。。。。。。我看到了这个

这个人的答案让我一惊，赶忙看了输出层的结果，每次输出的10维向量都是一样并且都无限接近与1，这不就印证了这位老哥的回答输入没有归一化。但我查看了数据的输入，784维的向量，发现都是不大于1的，这样问题不是出在输出上。

再想想，不是输入的问题，那不就是参数的问题，肯定是参数太大了。查看迭代过程中每层b向量的值，都很正常，绝对值都小于1。但是接下来转折来了，当我查看每层w矩阵值的时候，发现好多w的绝对值都到了5，6。这就找到问题了，w矩阵的值出了问题。

当时我瞬间想到是在初始化的时候出了问题，我刚开始写代码的时候还在纠结用np.random.rand()还是np.random.randn(),因为rand()生成的数据是在0-1之间，所有我选择了这个，没想到就是这一念之差，导致我后面几天心力交瘁。这也看到了合理初始化的重要性。