R-FCN论文详解
R-FCN
1、R-FCN 设计的目的
虽然Faster R-CNN把整个的检测过程集成到了一个可以end-to-end训练的网络，实现了大部分计算的共享，也极大的提高了检测速度。但是整个检测过程还是不够快，因为Faster R-CNN虽然使用了conv layers来共享特征提取，但是在RoI pooling提取每个RoI的feature map之后，要使用FC layer单独对每个RoI进行分类和回归，所以假设提取了128个RoI，那么就要使用FC layer进行128次的回归和分类，而且大家也都知道FC layer的计算量是非常大的，所以这部分的计算就拖慢了Faster R-CNN的检测速度。所以还需要更充分的共享计算才能再提高速度，因此文章中提出了使用全卷积网络(FCN, Fully Convolutional Network)来实现计算共享，提高速度。具体使用的是ResNet-101的conv layers。
但是使用这样比较深的网络也存在一个问题，那就是平移不变性和平移可变性的问题。因为使用ResNet-101分类的时候，无论物体怎么翻转、平移、扭曲，分类结果还是相同的，这就是平移不变性。但是对于目标检测，当物体发生平移时，检测结果也应该随着物体的变化而变化，这就是平移可变性。但是当卷积网络变深后，输出的feature map就变小，所以在原图上的一些物体的偏移，在经过N层pooling后得到的小feature map上会感知不到，所以网络变深使得平移可变性变差。所以为了解决这个问题，首先想到的是将RoI pooling层往前移动，因为在浅层的feature map上进行RoI pooling更能提取一些位置比较精确的proposal，然后这些proposal再进行卷积就能给深层的conv来平移可变性。对于这个改进，作者也给出了试验结果来证明：RoI放在ResNet-101的conv5后，mAP是68.9%；RoI放到conv4和conv5之间的mAP是76.4%，所以证明RoI能够给深层网络带来平移可变性，同时平移可变性对于目标检测也相当重要。**但是实验结果也表明，在conv5之后放RoI还是没有很好的效果，因此需要其他的方法来使得网络对于位置比较敏感，因此就提出了position-sensitive score map来达到这个目的，使得网络变深的同时，准确率也能和Faster R-CNN相媲美。
2、 R-FCN 的贡献
- 将FCN(Fully Convolutional Network)应用于Faster R-CNN，使得整个网络的计算可以共享，从而极大的提高了检测速度，同时检测的精度和性能(mAP)也可以和Faster R-CNN相媲美。
- 提出了position sensitive score map来平衡平移不变性(translation-invariance)和平移可变性(translation-variance)之间的矛盾。
3、 模型结构
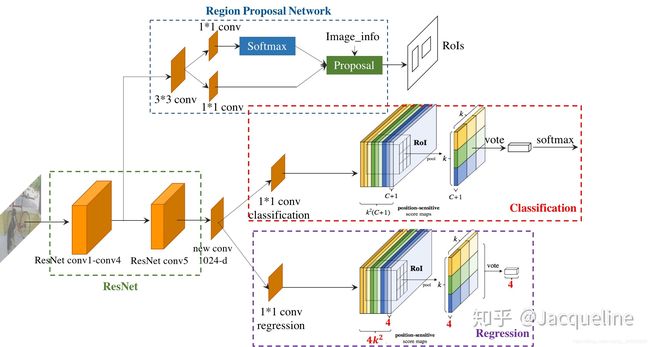
所示为R-FCN的结构图,从图中我们可以看出R-FCN主要包括4个部分：Conv layers (ResNet)、Region Proposal Network(RPN)、Classification、Regression。而整个R-FCN的流程如下：
- 首先输入一张图片，图片要经过resize使得图片的短边的长度为600。
- 然后图片先经过ResNet-101来提取特征，ResNet-101主要包括5个卷积网络块。
- 其中conv4的输出作为RPN的输入，和Faster R-CNN相同，这个RPN是用来提取proposal的，即提取出RoIs。
- 同时，ResNet-101的conv5输出因为是2048-d的，所以又加了一个新的new conv来降低channel的维度，输出的维度为1024-d。
- 然后这个1024-d的feature map再输入两个平行的conv layer中，一个用来classification，另一个用来regression。
- 对于classification的conv layer会产生一个 k 2 ( c + 1 ) k^2(c+1) k2(c+1) 维的position-sensitive score map，然后再结合RPN提取的RoIs进行pooling，之后再为每个RoI得到分类结果。
- 而对于regression的conv layer则会产生一个 4 k 2 4k^2 4k2 维的position sensitive score map，然后也同样结合RPN提取的RoIs进行pooling，之后再为每个RoI得到回归结果。
上述过程是R-FCN进行目标检测的一个流程，接下来给大家详细讲解R-FCN中的各个部分。
6.3.1 ResNet卷积层
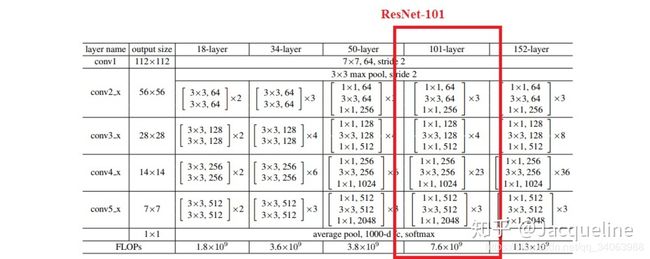
在R-FCN中采用的是ResNet-101的网络结构，ResNet-101主要包括5个conv块，其中包括100个的conv layer和1个FC layer，在文中去掉了最后一层FC layer，只使用了前5个conv块，共100层卷积。
6.3.2 Region Proposal Network(RPN)
R-FCN中的RPN和Faster R-CNN中的PRN相同，并没有进行改进，所以在此就不赘述了。
6.3.4 分类
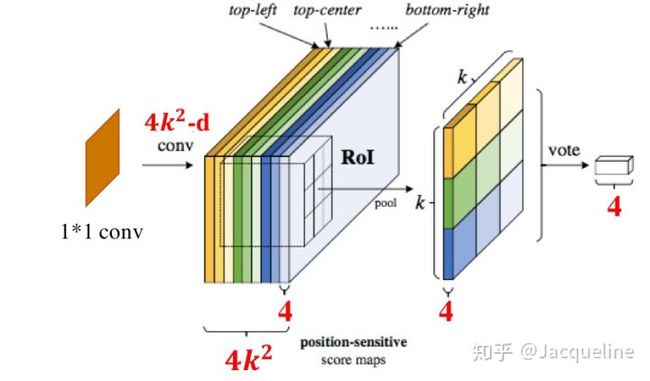
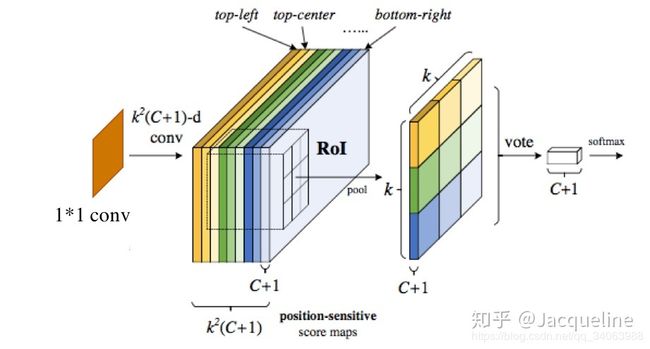
在分类模块中，new conv层输出的1024-d的feature map输入到一个 1 ∗ 1 1*1 1∗1 的卷积层中，然后得到一个 k 2 ( c + 1 ) k^2(c+1) k2(c+1) 维的position sensitive score map。 k 2 ( c + 1 ) k^2(c+1) k2(c+1) 表示有 k 2 k^2 k2 个score map，每个score map是 c + 1 c+1 c+1 维的，代表着 ( c + 1 ) (c+1) (c+1) 类。这 个 k 2 k^2 k2 score map都对应着 k ∗ k k*k k∗k 的网格的空间位置，第一个score map对应的是网格的top-left，第二个score map对应的是网格的top-center，依次类推。
得到这个position-sensitive score maps之后，就要结合RoIs来进行RoI pooling了，和Faster R-CNN相同的是，都会将RoI对应的feature map分成 k ∗ k k*k k∗k 个bin，然后在每个bin内进行pooling，然而不同的是R-FCN使用的是selective pooling。整个pooling过程可以用以下公式表示：
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-s421ntV0-1572844069178)(/Users/paulzyh/Git仓库/Papers_Reading/目标检测/图片/R-FCN_5.png)]](http://img.e-com-net.com/image/info8/0c1e98c9b7454b69962762412629f07a.jpg)
其中， ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 表示的是RoI的左上点的坐标， ( x , y ) (x,y) (x,y) 表示的是 b i n ( i , j ) bin(i,j) bin(i,j) 中的点的坐标，所以 ( x + x 0 , y + y 0 ) (x+x_0,y+y_0) (x+x0,y+y0)就是 b i n ( i , j ) bin(i,j) bin(i,j) 中的点在feature map上的坐标，然后 z i , j , c ( x + x 0 , y + y 0 ∣ Θ ) z_{i,j,c}(x+x_0,y+y_0|\Theta) zi,j,c(x+x0,y+y0∣Θ) 就是坐标对应的像素点的值，所以公式右侧的意思是 b i n ( i , j ) bin(i,j) bin(i,j) 中所有的像素点的值加和然后求平均，这就是说在 b i n ( i , j ) bin(i,j) bin(i,j) 中采用的是average pooling。这也就是说每个最后得到的 r c ( i , j ∣ Θ ) r_c(i,j|\Theta) rc(i,j∣Θ) 是用第 ( i , j ) (i, j) (i,j) 个score map上的第 ( i , j ) (i,j) (i,j) 个bin中进行average pooling得到。这个公式很绕，不懂也没关系，我们用图来说明。
如上图所示，对于一个RoI，首先将其分为 k ∗ k k*k k∗k 个bin，在这里为 3 ∗ 3 3*3 3∗3 ，也就是9个score map都应将RoI对应的区域分为 3 ∗ 3 3*3 3∗3 。那么在pooling时，第一个score map上的top-left bin中进行average pooling， 然后得到pooling后的feature map的左上角的值。然后第二个score map上的top-center bin 中进行average pooling，然后得到pooling后的feature map的top-center的值，依次类推。在图中，我使用了相同的颜色来表示进行average pooling的bin，以及其在pooling后的feature map上对应的位置。需要注意的是，在这里每个bin中使用的是average pooling，那使用max pooling也是可以的。
在pooling后得到的feature map其实就是文中提到的position-sensitive score，大小为 k ∗ k ∗ ( c + 1 ) k* k*(c+1) k∗k∗(c+1) ，每一类都有 k 2 k^2 k2 个position-sensitive score，然后用这 k 2 k^2 k2 个score对RoI进行投票，其实就是用每一类的 k 2 k^2 k2 个score进行加和求平均值，代表这一类的一个score：
r c ( Θ ) = ∑ i , j r c ( i , j ∣ Θ ) r_c(\Theta)=\sum_{i,j}r_c(i,j|\Theta) rc(Θ)=∑i,jrc(i,j∣Θ)
然后再用一个softmax进行分类，其实就是计算每一类的概率值：
s c ( Θ ) = e r c ( Θ ) / ∑ c ′ = 0 C e r c ′ ( Θ ) s_c(\Theta)=e^{r_c(\Theta)}/\sum_{c^{'}=0}^{C}e^{r_{c^{'}}(\Theta)} sc(Θ)=erc(Θ)/∑c′=0Cerc′(Θ)
至此，便完成了分类。
6.3.5 为什么是position-sensitive的
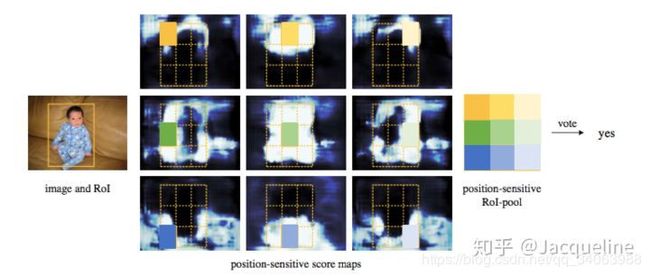
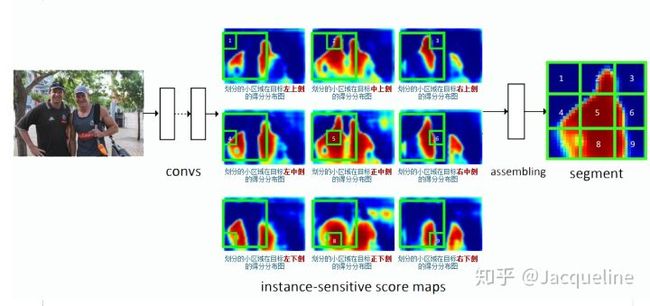
为什么position-sensitive score map能够带来平移可变性呢？要回答这个问题，我们首先要搞清楚position-sensitive score maps中每个像素点的值究竟代表什么意思。图5给出了一个score map的实例，图5中间的9张图便代表9个score map，分别代表左上、中上、右上等。以左上角的score map为例，这个score map上的每个点都代表了该点出现在目标左上角的概率(得分)，也就是说该点右下方刚好是目标物体的得分(score)。所以剩下的八张图依次代表图上的每个点出现在目标的正上方、右上方、左中方、正中方、右中方、左下方、正下方和右下方的概率(得分)。
搞清楚每个score map的点代表什么意思之后，我们来看在这些score map上是如何进行pooling的。 首先在每个score map上都找到RoI所对应的位置，并把这块区域分为 3 ∗ 3 3*3 3∗3 的网格 ，如图5中的绿色框所示。首先，我们从左上角的score map上取出左上角的 1 ∗ 1 1*1 1∗1 小格，左上角的score map代表了每个点出现在目标左上方的概率，因此我们取RoI左上角的 1 ∗ 1 1*1 1∗1 的小格的均值就代表了这个RoI左上角的部分出现在目标左上方的概率(得分)。之后我们从第二张图中取正上方的一个 1 ∗ 1 1*1 1∗1 的小格，第二张图上每一个点代表该点出现在目标正上方的概率(得分)，所以我们在这张图的RoI区域取正上方的 1 ∗ 1 1*1 1∗1 小格的均值，就代表了这个RoI正上方这部分出现在目标正上方的概率(得分)。以此类推，在第三张图上取右上方的小格子就代表了RoI右上方出现在目标右上方的概率(得分)。这样9个格子分别在9张score map上取得，然后就组成了一个完整的的 3 ∗ 3 3*3 3∗3 score map，这个score map就代表了RoI的各个区域出现在目标的概率(得分)。上图最右侧为最终组合出来的score map，我们可以看到它就是把各个部分的出现黑衣男的概率组合起来得到的一个概率分布图(score map)。当组合出来的9宫格score map对应ground truth时，小方格1就对应了ground truth左上角的位置，小方格2对应了ground truth正上方的位置，依此类推，所以用这种9宫格训练时就有了目标位置的信息在里面 。
6.4 Regression
Regression的过程和classification的过程大致一样，只不过是维度改变了一下。在regression的时候，同样先将new conv输出的feature map输入到一个 1 ∗ 1 1*1 1∗1的卷积层中，不过这个卷积层输出的维度是 4 k 2 4k^2 4k2 ，即得到维度为 $4k^2 $的position-sensitive score map，然后使用同样的方法进行pooling，得到 k ∗ k ∗ 4 k*k*4 k∗k∗4的一个score maps，这代表对于每一个位置，都有 k 2 k^2 k2 个score值，然后同样对这 k 2 k^2 k2个score求平均值，便得到一个4维向量，代表每个RoI需要偏移的位置，根据这4个值对RoI的位置进行调整，即可得到最红的bounding box的位置 t = ( t x , t y , t w , t h ) t=(t_x,t_y,t_w,t_h) t=(tx,ty,tw,th) 。
需要注意的是，regression对于每个RoI都值获得4个位置值，所有这4个值是和类别无关的，当然也可以让这些位置值和类别相关，这样就需要 1 ∗ 1 1*1 1∗1 卷积层的输出为 4 k 2 c 4k^2c 4k2c，这样每个类都会有对应的4个位置值。如果有不了解bounding-box regression的同学，可以参考我的这篇文章(Jacqueline：【目标检测】基础知识：IoU、NMS、Bounding box regression)。
至此，regression的过程也做完了。我们可以发现在classification和regression中，在RoI之后就米有需要学习的层了(no learnable layer)，因此这就使得RoI-wise的计算接近于cost-free，因为便可以极大的提高训练和测试的速度。
6.5 Training
在训练的过程中，可以使用预训练的ResNet-101网络和预先计算好的region proposals，这样就很容易训练end-to-end的R-FCN网络。然后R-FCN的loss函数的定义和Faster R-CNN也相同：
L ( s , t x , y , w , h ) = L c l s ( s c ∗ ) + λ [ c ∗ > 0 ] L r e g ( t , t ∗ ) L(s,t_{x,y,w,h})=L_{cls}(s_{c^*})+\lambda[c^*>0]L_{reg}(t,t^*) L(s,tx,y,w,h)=Lcls(sc∗)+λ[c∗>0]Lreg(t,t∗)
其中， c 2 c^2 c2 是RoI的ground-truth label，如果为0，那就代表是背景。 L c l s ( s c ∗ ) = − l o g ( s c ∗ ) L_{cls}(s_{c^*})=-log(s_{c^*}) Lcls(sc∗)=−log(sc∗) 是定义分类的cross-entropy loss。 L r e g L_{reg} Lreg 是回归的损失，定义和Fast R-CNN中的相同，其中 t ∗ t^* t∗ 代表ground-truth bounding box。 [ c ∗ > 0 ] [c^*>0] [c∗>0] 是一个指示器，当 c ∗ > 0 c^{*}>0 c∗>0 的时候为1，否则为0。 λ \lambda λ 为1。此外，在训练时，如果RoI和ground-truth box的 IoU大于0.5，那么为正样本，否则为负样本。
6.6 Inference
在测试时，会为每张图片提取300个RoIs，然后最终得到的bounding box需要通过非极大值抑制(NMS)来进行筛选，在NMS的过程中把IoU的阈值设为0.3。 如果有不了解NMS的同学，可以参考我的这篇文章(Jacqueline：【目标检测】基础知识：IoU、NMS、Bounding box regression)。
6.7 空洞卷积／膨胀卷积(atrous convolution)
在R-FCN中将ResNet的conv5的strides从2变成1，使得resnet-101的有效跨距从32像素减少到16像素，从而提高了score map的分辨率，同时，为了弥补strides的减小，在conv5部分使用空洞卷积。
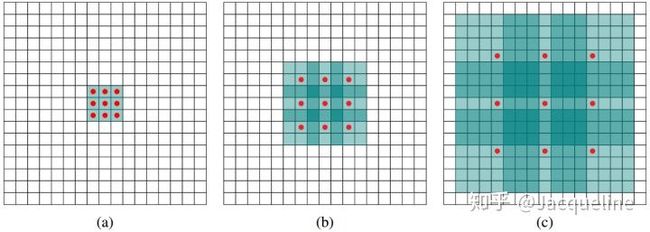
其中，图(a)是kernel size为 3 ∗ 3 3*3 3∗3 的1-dilated conv，这和普通的卷积操作一样。图(b)对应的是kernel size为 3 ∗ 3 3*3 3∗3的2-dilated conv，由于空洞为1，所以进行卷积时，会隔一个点进行卷积，感受野将变为 7 ∗ 7 7*7 7∗7 ，如图所示只有9个红色的点和 3 ∗ 3 3*3 3∗3 的kernel发生卷积操作，其余的点略过。图©是kernel size为的 3 ∗ 3 3*3 3∗3 4-dilated conv，这时就可以达到 15 ∗ 15 15*15 15∗15的感受野。所以和传统的卷积操作，空洞卷积可以扩大感受野，让卷积层的输出包含更大范围的信息。注意，在R-FCN中只在ResNet的conv5部分使用了空洞卷积。
6.8 总结
本篇文章结合Faster R-CNN和FCN，提出了一个简单高效的R-FCN网络，它可以达到与Faster R-CNN几乎相同的检测精度，但速度却比Faster R-CNN快2.5-20倍。所以整个网络总结起来就是简单、快速、高效。