Leetcode刷题之二叉树（一）

一、二叉树的最大深度（104）

1、问题

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

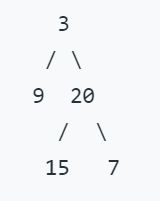
返回它的最大深度 3 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree

2、解答

解法一：递归方法：树的前序遍历（类比于图的深度优先搜索算法DFS）。
官方示例

二叉树遍历（前序、中序、后序、层次、深度优先、广度优先遍历）

图的广度优先搜索（BFS）和深度优先搜索（DFS）算法解析

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import java.lang.Math;
class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;//递归头
        }else{ //递归体
            int left = maxDepth(root.left);
            int right = maxDepth(root.right);
            return Math.max(left,right)+1; //每次向下成功搜索加1
        }
    }
}

解法二：迭代方法，利用栈

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import javafx.util.Pair; //相当于python中的二元组
import java.lang.Math;
class Solution {
    public int maxDepth(TreeNode root) {
        //迭代法
        Stack> stack = new Stack<>();
        if(root!=null){
            stack.push(new Pair(root,1));
        }
        int depth = 0;
        while(!stack.isEmpty()){
            Pair current = stack.pop();
            root = current.getKey();
            int current_depth = current.getValue();
            if (root != null) {
                depth = Math.max(depth, current_depth);
                stack.push(new Pair(root.left, current_depth + 1));
                stack.push(new Pair(root.right, current_depth + 1));
            }
        }
        return depth;
    }
}

二、二叉树的最小深度（111）

1、问题

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

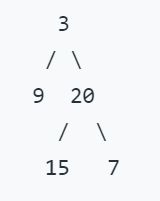
返回它的最小深度 2.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-depth-of-binary-tree

2、解答

递归方法：
递归终止的条件：空节点，返回0；当 root 节点左右子树都为空时（叶子），返回 1；左右子树有一个为空时，返回不为空的子树的深度；左右子树都存在时，返回左右子树深度较小的节点的
这和求最大深度有点不同，最大深度不用考虑有一个子树为空的情况，max(m1,m2)+1已经包括了这个情况。
求最小深度，要考虑这种特殊情况，这里应该考虑的是非空子树的深度，用min(m1,m2)取得的是0，它忽略了非空子树的深度，这里应该返回m1+m2+1;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if(root == null){
           return 0; 
        }else{ 
        int m1 = minDepth(root.left);
        int m2 = minDepth(root.right);
        return root.left==null||root.right==null?m1+m2+1:Math.min(m1,m2)+1;
        }
    }
}