字符串匹配算法初探
近日刷题,遇到诸多关于字符串匹配的问题。再次打开CLRS,学习字符串匹配该章,又有感受良多。
要弄清字符串匹配的过程,需先明确以下几个定义:
1.匹配串(文本):待匹配的字符串,是一个长度为n的字符数组T[1..n]
2.模式串:匹配的基准串,是一个长度为m的字符数组P[1..m],其中m≤n
3.有效位移:若存在位移s∈[0,n-m],且T[s+1..s+m]=P[1..m],那么就说明模式P在文本T中出现且位移为s,此时称s为一个有效位移,否则称s为一个无效位移
许多字符串匹配算法的基本流程主要分为两大部分:预处理和匹配。而区分匹配效率的关键在于不同算法的匹配策略。
特此说明:下述讲解中存在文本和模式的数组下标,一概从1开始;代码中实现仍是从0开始。
首先看朴素字符串匹配算法,也称为暴力匹配算法(BF)。
核心在于滑动窗口的移动速率只有一位,只要模式与文本在某字符位置k不匹配,下一次匹配就要从文本的k+1位置开始,而模式串则要从头匹配。这样很明显是耗费大量时间的。比如下图中文本为acaabc,模式为aab,s为匹配的指针位置: 
当s=1时,文本T[2]=c,而模式P[2]=a不匹配, 此时下一次匹配的滑动窗口向后移动一位,从T[3]=a开始,而对应的模式P应从头开始匹配。该匹配算法虽然没有预处理过程,但是匹配时间为O((n-m+1)m),倘若m=n/2,那么时间复杂度将变为O(n²)。
伪代码为:
NAIVE-STRING-MATCHER(T,P)
1 n ← length[T]
2 m ← length[P]
3 for s ← 0 to n-m
4 do if P[1..m]=T[s+1..s+m]
5 then print "Pattern occurs with shift" s
C++代码实现如下:
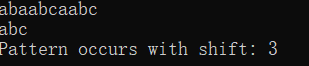
//只匹配第一次出现的字符串
int Naive_String_Matcher(string T,string P){//T为匹配串,P为模式串
int n=T.size();
int m=P.size();
for(int s=0;s若文本中存在多处位置与模式匹配,应该将上述代码略加修改
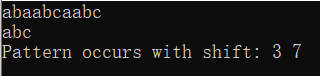
//匹配多次出现的字符串
vector Naive_String_Matcher_More(string T,string P){//T为匹配串,P为模式串
int n=T.size();
int m=P.size();
vector pos;
for(int s=0;s 拓展1:假设模式P中的所有字符都是不同的。试说明如何对一段n个字符的文本T加速过程NAIVE-STRING-MATCHER的执行速 度,使其运行时间为O(n)。
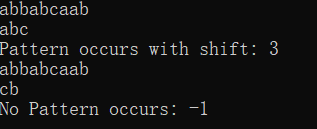
分析:若文本T与模式P匹配,则必有P[1..m]=T[s+1..s+m]。当确定匹配时,一定存在T[s+2..s+m]中的每一个字符都不同且不等于T[s+1],即c∈T[s+2..s+m] 且 c≠P[1]。若T[s+m+1]≠P[m+1],下一次比较应该直接从T[s+m+1]开始而非T[s+2]。
用一个例子来说明,文本为abbabcaab,模式为abc,例图如下:
C++代码如下:
int Naive_String_Matcher_unique(string T,string P){//T为匹配串,P为模式串
int n=T.size();
int m=P.size();
int k=0;
for(int s=0;s0) s--; //一定要做修正,若当前字符不匹配且前一个字符匹配时,匹配串应从当前字符与模式串从头匹配,而不是从下一个字符匹配
k=0;
}
}
cout<<"No Pattern occurs: ";
return -1;
}
拓展2:假设允许模式P中包含一个间隔字符#,该字符可以与任意的字符串匹配(甚至可以与长度为0的字符串匹配)。例如, 模式ab#ba#c在文本cabccbacbacab中的出现为
c ab cc ba cba c ab
ab # ba # c
或
c ab ccbac ba c ab
ab # ba # c ab
我们假定间隔字符#不会出现在文本中,却可能在模式中出现任意次。试给出一个多项式运行时间的算法,已确定这样的 模式P是否出现于给定的文本中。
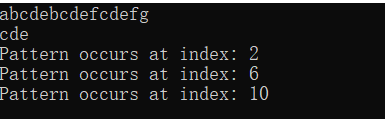
分析:将模式串P按照#分割成k个子串P1,P2,...Pk,后在匹配串T中使用朴素字符串算法查找这k个部分,如果查找到Pi时,就从匹配位置的后一位开始查找Pi+1。
C++代码如下:
bool Naive_String_Matcher_IntervalCharacter(string T,string P){//T为匹配串,P为模式串
int n=T.size();
int m=P.size();
vector v=spilt(P,"#");
vector vt;
vt.push_back(T);
int pos=0;
string tmp;
bool flag=true;
for(int i=0;i spilt(const std::string &str, const std::string &delim)
{
std::vector spiltCollection;
if(str.size()==0)
return spiltCollection;
int start = 0;
int idx = str.find(delim, start);
while( idx != std::string::npos )
{
spiltCollection.push_back(str.substr(start, idx-start));
start = idx+delim.size();
idx = str.find(delim, start);
}
spiltCollection.push_back(str.substr(start));
return spiltCollection;
}
然后来谈谈Rabin-Karp算法。
该算法相对朴素字符串匹配算法而言,是对每个字符进行对应进制数并取模运算,类似于通过某种函数计算其函数值,比较的是每个字符的函数值。预处理时间O(m),匹配时间是O((n-m+1)m)。
伪代码为:
RABIN-KARP-MATCHER(T,P,d,q)
1 n ← length[T]
2 m ← length[P]
3 h ← d^(m-1) mod q
4 p ← 0
5 t ← 0
6 for i ← 1 to m
7 do p ← ( dp + P[i] ) mod q
8 t ← ( dt + T[i] ) mod q
9 for s ← 0 to n-m
10 do if p = t
11 then if P[1..m]=T[s+1..s+m]
12 then print "Pattern occurs with shift" s
13 if s < n - m
14 then t ← ( d ( t - T[s+1] h ) + T[s+m+1] ) mod q
C++代码如下:
//Rabin-Karp算法
void Rabin_Karp_Matcher(string T,string P,int d,int q){//d=10,q=13
int n=T.size();
int m=P.size();
int h=(int)pow(d,m-1)%q;
long long p=0,t=0,k;//只能将模式串P长度保持在9个以内
for(int i=0;i参考来源:http://www.geeksforgeeks.org/searching-for-patterns-set-3-rabin-karp-algorithm/