机器学习之线性回归(机器学习基石)
引子
在一个二元分类的问题中我们通常得到的结果是1/0,而在分类的过程中我们会先计算一个得分函数然后在减去一个门槛值后判断它的正负若为正则结果为1若为负结果为0。
事实上从某种角度来看线性回归只是二元分类步骤中的一个截取它没有后面取正负号的操作,它的输出结果为一个实数而非0/1。我们称这样的数学模型为线性回归。
在传统上统计学家给出的结果是如下:
它的物理意义就是要提取多笔资料的特征用一个线性的函数所表示,我们要做的就是让我们资料的表现与我们函数之间的差距之和越小越好。进一步来说我们就是要找一个h(x)通过调整它的权重W来达到上述目的。(当然此时的W的维度包括常数在内)
几何意义
图中的点代表我们资料的表现,而那条蓝色的线就是我们的h(x),每个点到线(或者超平面)的距离就是资料与我们线性模型的误差。我们的目的就是使得所有点到线的距离之和最小。
传统上我们的线性回归的误差计算为平方误差表现为下图:
进一步来说我们模型所犯的错误如下图所示:
左图中是模型h(x)在样本上犯的错误,右边是模型h(x)在总体数据上犯的错误,我们相信在VC维度的保障下我们可以从大量的数据中学到东西。也就是我们在大量数据下学习使得我们的模型的Ein很小就是我们下一步要完成的目标。
如何最小化Ein
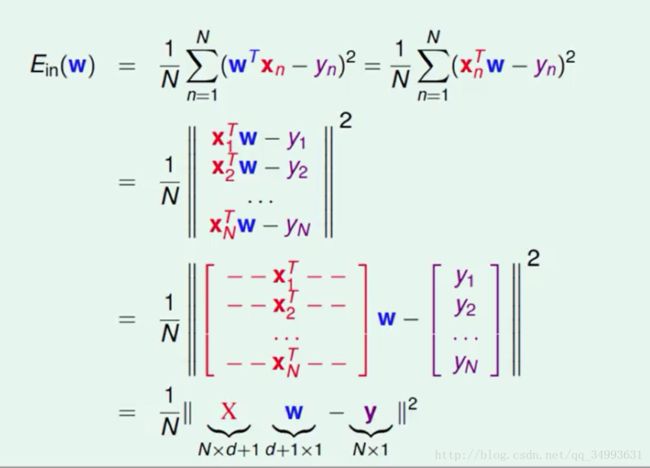
Ein的矩阵表示
由于一个h(x)对应的一个W向量而其他的x与y都为已知量所以我们对h(x)的优化也就是我们对W的优化所以下面的推到中只有W为变量:
经过一系列的推导我们将Ein写成了更为直观的矩阵的形式,我们要求的就是Ein最小时W的值是多少。经过一些数学上的推导我们发现Ein对应的函数是一个凸函数(大陆好像一般都是凹函数)如下图所示:
根据凸函数的性质我们可以知道在函数的梯度为0的时候我们可以得到函数的最小值,也就是我们要求的W正是Ein的梯度为0的时候所对应的W。
Ein梯度的表示与W的计算
上图从一维的w(单一变数)推广到了多维的W(向量)最后得到了最终的梯度表达式如上图下方所示。
令梯度为0我们可以得到W:
在上图的上方我们得到了最优的W的表达式,在大多数的情况下X的转置与X的乘积是有反矩阵的此时的W可以一步计算出来(它只有一个解)如上图左方所示,在不是反矩阵的情况下我们也会求出一个假的反矩阵来这个假的反矩阵与反矩阵有类似的性质(这种情况下会有多组解我们会选择其中的一组解)如上图右方所示。在实务上很多的软件都写好了求(假的)反矩阵的包我们可以直接调用。
这样我们就求出了最优的W,同时也求出了最优的h(x)。
线性回归的算法看起来像是一步登天没有经过看起来一步一步的学习,但是在整个过程中在最后Eout≈0我们说这个算法确实发生了学习只是学习的步骤隐藏起来了(如果我们编写一个程序就有直观的感受我们会有一次一次的迭代)。
Ein的另一种表现形式
H矩阵的意义
如上图所示Ein可以用一个含有杂讯的式子来表示,在上图的式子中我们将y矩阵与他的线性变换分离开来我们得到了H矩阵。现在已知Hy = y hat(y上面加^),从线性代数的基础知识中我们知道H是一个y的线性变换如下图所示:
在图中粉红色部分为X矩阵展开的线性空间而y hat = XWlin所以y hat也在X矩阵所展开的线性空间上,而已知y在X的线性空间外则y - y hat 的向量的大小就是y与X空间上最近的距离(因为我们的y hat是一个最优解)。又知道y与y在X空间投影的距离最小,那么我们就知道y hat就是y在X空间上的投影。也就是我们的H矩阵是y到X空间的投影动作。同时也知道了(I - H)是y在X空间上取余数的动作(由y得到y-yhat的线性变换)。
如果我们用力计算的话我们会得到trace(I - H) = N - (d + 1),其中trace是矩阵对角线之和。它的物理意义是什么N个自由度的向量(x向量的个数与y向量维度都是N)投影到一个d+1维的空间里(x向量的维度)再经过取余数之后会得到余数的自由度为
N-(d+1),也就是y - y hat的维度。
Ein的另一种表现形式
在上图上线性代数告诉我们我们的目标函数也在X空间中,而我们的标签y正是f(x)+noise的结果,而在加上我们讨论过的线性变换我们就会得出y - y hat = (I - H)noise,加上我们的trace(I - H) = N - (d + 1),在加上我们对noise做平均得到noise level,最后将这些结论带入以前的Ein表达式得到一个全新的Ein表达式如上图下方所示。与此同时Eout也可以采用类似的算法来计算只是相对困难如上图下方所示。
学习曲线
在经过上述的推导之后我们得到了如下曲线:
他描述了我们的资料量与我们平均可以的得到平均的Ein与Eout的关系,我们可以看出随着资料量的增大Ein的平均与Eout的平均越来越接近,而且如果在杂讯很小的情况下我们就能办到Eout≈0,此时我们学到了东西。
最后再次感谢林轩田老师,更多关于机器学习的内容请关注智能时代的道与术。