论文研读笔记(二)——VGG
论文研读系列汇总:
1.AlexNet论文研读
2.VGG论文研读
3.GoogLeNet论文研读
4.Faster RCNN论文研读
5.ResNet 论文研读
6.SENet 论文研读
7.CTPN 论文研读
8.CRNN 论文研读
论文基本信息
论文题目为:
Very Deep Convolutional Networks for Large-Scale Image Recognition
作者:
Karen Simonyan & Andrew Zisserman
论文原文:
https://arxiv.org/pdf/1409.1556.pdf
论文研读内容:
摘要:
1.这篇论文探究了卷积神经网咯的深度对大规模图像识别精度的影响。
- 作者评估了使用更小卷积核3*3的好处。3*3既考虑跨通道,也考虑局部信息整合
- 主要是在深度上进行提高,结果显示当网络层数达到16-19层时网络效果提升明显。
- 1*1不仅能改变维度大小,也能专注于那一个卷积核内部通道的信息整合。
- ALEXNET中LRN的用处不大
- 多裁剪图像评估与密集卷积评估有互补的关系,并且作者假设这是由于卷积边界的条件不同处理造成的
- 全连接层转卷积层。使网络对任意大小的输入都可以处理。
Muti-scale(多尺度):
首先对原始图片进行等比例缩放,使得短边要大于224,然后在图片上随机提取224x224窗口,进行训练。由于物体尺度变化多样,所以多尺度(Multi-scale)可以更好地识别物体。
VGG网络第一次在神经网络的训练过程中提出也要来搞多尺寸。目的是为了提取更多的特征信息。
VGG的特点:
1.小卷积核。作者将卷积核全部替换为3x3(极少用了1x1);
2.小池化核。相比AlexNet的3x3的池化核,VGG全部为2x2的池化核;
3.层数更深特征图更宽。基于前两点外,由于卷积核专注于扩大通道数、池化专注于缩小宽和高,使得模型架构上更深更宽的同时,计算量的增加放缓;
4.全连接转卷积。网络测试阶段将训练阶段的三个全连接替换为三个卷积,测试重用训练时的参数,使得测试得到的全卷积网络因为没有全连接的限制,因而可以接收任意宽或高为的输入。
关键词:尺度抖动 多尺度训练 归一化 密集评估
1.介绍:
之前人们一直尝试在AlexNet的原始框架上做一些改进,像是在第一个卷积上使用较小的卷积核以及较小的滑动步长,另一种思路就是在全图以及多个尺寸上,更加稠密的进行训练和测试网络.(作者在后面也有对这个改进的实验与分析)
图片出自:https://www.jianshu.com/p/74cebed0b4f8
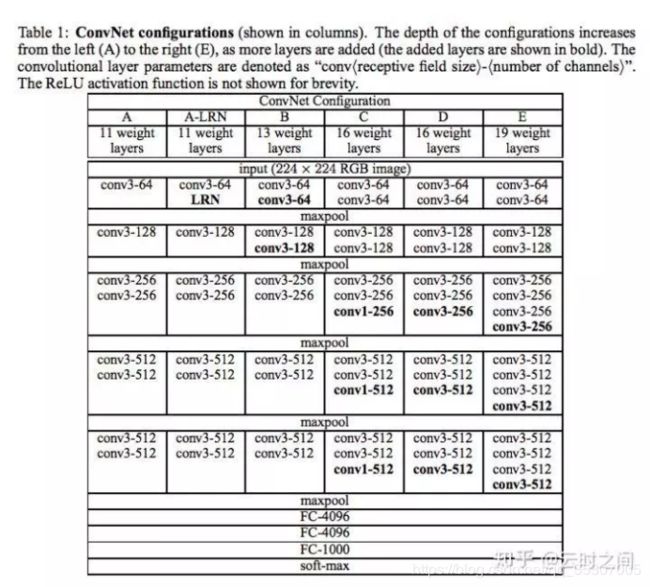
VGG模型主要关注的是网络的深度,因此文章固定了网络的其他参数,通过增加卷积层来增加网络的深度,这个网络的深度是当时在论文发表前最深的深度网络。
- 卷积配置
在这一个章节,先是介绍卷积网络的通用架构,再去描述其评估的具体细节,最后再和之前的网络进行比较.主要是对卷积配置的一种介绍
a):架构
训练输入:固定尺寸224*224的RGB图像。
预处理:每个像素值减去训练集上的RGB均值。(全部工作仅这一个预处理)
卷积核:一系列3*3卷积核堆叠,步长为1,采用padding保持卷积后图像空 间分辨率不变。
空间池化:紧随卷积“堆”的最大池化,为2*2滑动窗口,步长为2。
全连接层:特征提取完成后,接三个全连接层,前两个为4096通道,第三个为1000通道,最后是一个soft-max层,输出概率。
所有隐藏层都用非线性修正ReLu.
b):详细配置
VGG各种级别的结构都采用了5段卷积。VGG的之所以能够达到更高的精准性,源自于卷积层的更多的Channel数。而由于filter size的减小,channel可以大幅度增加,更多的信息可以被提取,channel数增加提高了提取特征的复杂度。而通过max-pooling能减小宽度和高度,从而忽略局部小特征,更容易捕捉图像上的变化,梯度的变化,带来更大的局部信息差异性,更好地描述边缘、纹理等构成语义的细节信息,这点尤其体现在网络可视化上。
特征图的宽高从512后开始进入全连接层,因为全连接层相比卷积层更考虑全局信息,将原本有局部信息的特征图(既有width,height还有channel)全部映射到4096维度。换句话说全连接要将信息压缩到原来的五分之一。VGGNet有三个全连接,我的理解是作者认为这个映射过程的学习要慢点来,太快不易于捕捉特征映射来去之间的细微变化,让backprop学的更慢更细一些(更逐渐)。
feature map维度的整体变化过程是:先将local信息压缩,并分摊到channel层级,然后无视channel和local,通过fc这个变换再进一步压缩为稠密的feature map,这样对于分类器而言有好处也有坏处,好处是将local信息隐藏于/压缩到feature map中,坏处是信息压缩都是有损失的,相当于local信息被破坏了(分类器没有考虑到,其实对于图像任务而言,单张feature map上的local信息还是有用的)。
3*3 filter的好处:
VGG经常出现多个完全一样的3×3的卷积核堆叠在一起的情况,这些多个小型卷积核堆叠的设计其实是非常有效的。
两个3×3的卷积层串联相当于1个5×5的卷积层,即一个像素会和周围5×5的像素产生关联,可以说感受野是5×5。同时,3个串联的3×3卷积层串联的效果相当于一个7×7的卷积层。除此之外,3个串联的3×3的卷积层拥有比一个7×7更少的参数量,只有后者的 (3×3×3) / (7×7) = 55%。最重要的是3个3×3的卷积层拥有比一个7×7的卷积层更多的非线性变换(前者可以使用三次ReLu(非线性激活函数)激活,而后者只有一次)。
简言之,越小的卷积能获得更多的非线性变换,提取更多强有力的特征,而且在不降低感受野的情况下,能减少参数量。
3.分类框架
a):训练
训练方法基本与AlexNet一致,除了多尺度训练图像采样方法不一致。
训练采用mini-batch梯度下降法,batch size=256;
采用动量优化算法,momentum=0.9;
采用L2正则化方法,惩罚系数0.00005;
dropout比率设为0.5;
初始学习率为0.001,当验证集准确率不再提高时,学习率衰减为原来的0.1 倍,总共下降三次;
总迭代次数为370K(74epochs);
数据增强采用随机裁剪,水平翻转,RGB颜色变化;
设置训练图片大小的两种方法:
Ps:定义S代表训练图像的尺度(大小)。
第一种方法针对单尺寸图像训练,S=256或384,输入图片从中随机裁剪 224*224(384*384)大小的图片。
第二种方法是多尺度训练,实验中,作者令S在[256, 512]这个区间,随机取训练尺度,并进行图片训练,可以理解为训练尺度的尺度抖动,以提高提取特征的复杂性
论文中提到,网络权重的初始化非常重要,由于深度网络梯度的不稳定性, 不合适的初始化会阻碍网络的学习。因此作者先训练浅层网络(A),再用训练好的浅层网络(A)去初始化深层网络。(这里作者用A模型的参数初始化后面的参数,这其实是一种人为的方式,并提到现在可以用随机初始化来初始而不用预训练)
b):测试
测试阶段,对于已训练好的卷积网络和一张输入图像,采用以下方法分类:
1.图像被归一化到测试尺寸Q,测试尺寸不一定等于训练尺寸(博主个人理解:若为多尺度,测试尺寸不一定等于训练尺寸);
2.将原先的全连接层改换成卷积层,在未裁剪的图像上运用卷积网络。在最后一个卷积层使用滑窗的方式进行分类预测,将不同窗口的分类结果平均,再将不同尺寸Q的结果平均,得到最后的结果。这样可以提高数据的利用率和预测准确率。输出是一个与输入图像尺寸相关的分类得分图(输出通道数与类别数和输入图像大小的可变空间分辨率有关)
3.我们同样对测试集做数据增强,采用水平翻转,最终取原始图像和翻转图像 的soft-max分类概率的平均值作为最终得分。
4.使用多个裁剪图像,能提高采样的精细程度,而利用全卷积的密集评估能增大感受野,从而捕获更多上下文信息。一个增加细致度,另一个增加联系度。从而达到互补的目的。
另外在某篇博客找到了卷积层与全连接层之间的关系:
卷积层和全连接层的唯一区别在于卷积层的神经元对输入是局部连接的, 并且同一个通道(channel)内不同神经元共享权值(weights). 卷积层和全连接层都是进行了一个点乘操作, 它们的函数形式相同. 因此卷积层可以转化为对应的全连接层, 全连接层也可以转化为对应的卷积层.
比如VGGNet[1]中, 第一个全连接层的输入是7∗7∗5127∗7∗512, 输出是4096. 这可以用一个卷积核大小7∗77∗7, 步长(stride)为1, 没有填补(padding), 输出通道数4096的卷积层等效表示, 其输出为1∗1∗40961∗1∗4096, 和全连接层等价. 后续的全连接层可以用1x1卷积等效替代. 简而言之, 全连接层转化为卷积层的规则是: 将卷积核大小设置为输入的空间大小.
这样做的好处在于卷积层对输入大小没有限制, 因此可以高效地对测试图像做滑动窗式的预测. 比如训练时对224∗224224∗224大小的图像得到7∗7∗5127∗7∗512的特征, 而对于384∗384384∗384大小的测试图像, 将得到12∗12∗51212∗12∗512的特征, 通过后面3个从全连接层等效过来的卷积层, 输出大小是6∗6∗10006∗6∗1000, 这表示了测试图像在36个空间位置上的各类分数向量. 和分别对测试图像的36个位置使用原始的CNN相比, 由于等效的CNN共享了大量计算, 这种方案十分高效而又达到了相同目的.
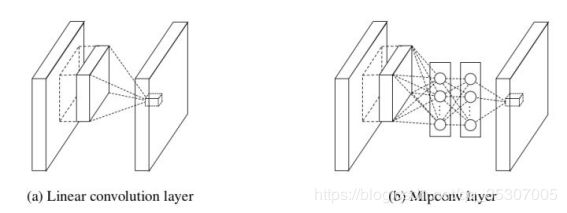
全连接层和卷积层的等效表示最早是由[2]提出. [2]将卷积层中的线性核改成由一系列的全连接层组成的小神经网络, 用于在每个卷积层提取更复杂的特征. 在实现时, NIN是由一个传统卷积层后面加一系列1*1卷积得到的.
[3]论证了用卷积层替代全连接层的好处, 下图黄色部分是多出来的计算量, 和将一个网络运用在测试图像的多个位置相比, 这种方法十分高效.
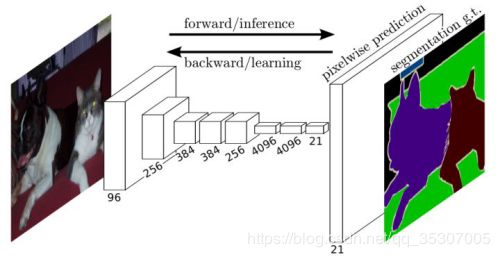
由于卷积层可以处理任意大小输入, 非常适合检测, 分割等任务, 比如[4]提出全卷积网络用于进行语义分割.
根据论文结构创建VGG16网络
代码见https://www.jianshu.com/p/68ac04943f9e
参考博客汇:
链接:https://www.jianshu.com/p/74cebed0b4f8
链接:https://www.jianshu.com/p/68ac04943f9e
链接:https://blog.csdn.net/xz1308579340/article/details/79850248
链接:https://www.cnblogs.com/kk17/p/9792071.html
强推此博客VGG模型核心拆解
链接:https://blog.csdn.net/qq_40027052/article/details/79015827