LeetCode练习题802. Find Eventual Safe States

题目

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph.  If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node.  More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe?  Return them as an array in sorted order.

The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph.  The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
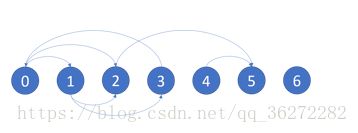
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Here is a diagram of the above graph.

Note:

• graph will have length at most 10000.
• The number of edges in the graph will not exceed 32000.
• Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

 

思路

这道题的实质是利用深度优先算法遍历这个图，然后判断以某一点为起点时是否存在环，若不存在环，则该起点是安全的。

首先用state数组标明每个节点的状态，0表示未访问过，1表示访问过且是安全的，2访问过且不安全。初始时，每个节点的状态为0，即未访问过。

然后声明一个深度优先遍历函数 如下所示：

bool oneNodePath(vector>& graph, int start, vector& state)

函数的第一个参数为原图graph，第二个参数为遍历起始的点，第三个参数为所有点的状态.。

因为图有可能不是连通图，对每个点都需要遍历，所以在eventualSafeNodes函数中利用for循环对每个点进行深度优先遍历。如下代码所示：

        for (int i = 0; i < len; i++) {
            if (oneNodePath(graph, i, state)) {
                result.push_back(i);
            }
        }

在深度优先遍历函数oneNodePath中，遍历到的点，若它状态为0，就将它修改为2，然后对它的子节点进行遍历。若便利完子节点都没发现有环，说明该节点是安全的，则修改状态为1，否则是不安全的，保持状态为2。

 

代码

class Solution {
public:
    bool oneNodePath(vector>& graph, int start, vector& state) {
        if (state[start] == 0) state[start] = 2;
        else if (state[start] == 1) return true;
        else if (state[start] == 2) return false;
        for (int i = 0; i < graph[start].size(); i++) {
            if (oneNodePath(graph, graph[start][i], state) == false) return false;
        }
        state[start] = 1;
        return true;
    }
    //state代表节点状态,0表示未访问过，1表示访问过且是安全的，2访问过且不安全
    vector eventualSafeNodes(vector>& graph) {
        int len = graph.size();
        vector result;
        vector state;
        //全部初始化为未访问
        for (int i = 0; i < len; i++) {
            state.push_back(0);
        }

        for (int i = 0; i < len; i++) {
            if (oneNodePath(graph, i, state)) {
                result.push_back(i);
            }
        }
        return result;
    }
};