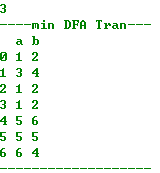
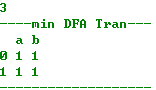
【编译原理】实验三 NFA 确定化和 DFA 最小化
一、实验标题:NFA确定化和DFA最小化
二、实验目的:
1. 学习和掌握将NFA转为DFA的子集构造法。
2. 学会编程实现等价划分法最小化DFA。
三、实验内容:
(一)NFA确定化
(1)确定NFA与DFA的存储格式。
要求为3个以上测试NFA准备好相应有限自动机的存储文件。
(2)用C或JAVA语言编写将NFA转换成DFA的子集构造法的程序。
(3)测试验证程序的正确性。
(4)测试用例参考:将下列语言用RE表示,再转换成NFA使用:
(a) 以a开头和结尾的小字字母串;a (a|b|…|z)*a | a
(b) 不包含三个连续的b的,由字母a与b组成的字符串;(e | b | bb) (a | ab | abb)*
(c) (aa|b)*(a|bb)*
(二)DFA最小化
(1)准备3个以上测试DFA文件。(提示:其中一定要有没有最小化的DFA)
(2)DFA手动完善。(状态转换映射要是满映射)
(3)用C或JAVA语言编写用等价划分法最小化DFA的程序。
(4)经测试无误。测试不易。可求出两个DFA的语言集合的某个子集,再证实两个语言集合完全相同!
四、系统设计:
1. 主程序流程
Ø 概述:通过实例化NFAtoDFA类声明测试对象test。对test初始化,选择使用样例1、2、3初始化test中的NFA。初始化结束后,可以多次选择打印NFA状态转换表、打印DFA状态转换表、打印minDFA状态转换表;退出后,可以选择打印对应语言集。输入len,分别输出长度≤len的NFA语言集、DFA语言集、minDFA语言集以验证NFA、DFA、minDFA描述了同一种语言。
Ø 流程图:
1. 算法的基本思想
Ø 概述:算法主要分为四个部分:NFA的存储、NFA转换为DFA、DFA最小化为minDFA 与 检验NFA、DFA和minDFA描述了同一语言;
v NFA转换为DFA使用子集构造算法,其中包含两个重要函数:
² closure(T):状态集合T的闭包
² move_Tc(T,c):状态集合T在输入符号为c的情况下转入目标状态的集合
v DFA最小化为minDFA使用等价划分算法。
² 获得minDFA状态集合
² 构造minDFA状态转换表minDtran
v 检验部分通过对比NFA、DFA和minDFA的长度小于等于N的语言集合相同证明三个状态转换图等效。
² 递归输出语言集合
Ø NFA的存储
从文件中读取一个NFA的要素:符号个数、符号集合、状态个数、接受状态个数、接受状态集合以及状态转换表。
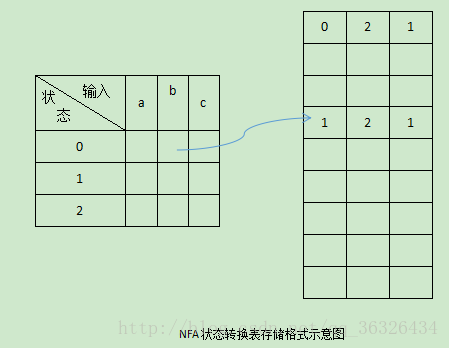
状态转换表较为特殊,因为NFA的状态允许在同一输入符号下可以到达多个目标状态,那么完整的状态转换表则需要一个三维数组。在此次实验中,选用二维数组去存储状态转换表。数组内存储的是一个向量,在向量内存储每一个状态在对应输入符号下可能达到的状态,如下图所示:
在读取NFA状态转换表时,只需要获取对应数组中的向量,再遍历向量即可找到对应的状态序列。
下表中为NFA输入文件存储格式:
2 //字符个数
a b //字符集合
12 //状态个数
11 //接受状态编号
-1 -1 1,11 //从此行开始为状态转换表
-1 -1 2,6 //列为输入符号
-1 -1 3 //行为状态编号
4 -1 -1 //内容为对应状态下对应输入符号会
-1 -1 3,5 //转化到的状态列表
-1 -1 2,10
-1 -1 7
-1 8 -1
-1 -1 7,9
-1 -1 6,10
-1 -1 1,11
-1 -1 -1
Ø 子集构造算法:
算法思想:为DFA构造一个状态转换表Dtran。DFA的每个状态是一个NFA的状态集合。在构造Dtran的过程中,使得DFA模拟NFA在遇到一个给定输入串时可能执行的所有动作。
①以NFA开始状态的闭包(状态的集合)作为DFA的开始状态。
②如果DFA的状态集合中存在一个状态T,T还没有模拟NFA构造过Dtran,那么对于该状态T,依次检查输入符号表。T在输入符号a下,所包含的所有NFA的状态可以到达的状态集合构成DFA状态U。
③检查U是否为DFA的某一个状态。如果不是,那么就将该状态U加入到DFA的状态集合中。如果是,直接进入下一步。
④构造DFA的状态转换表Dtran,即对于当前状态T,经过输入符号为a的转换后可以到达状态U。
⑤回到②步骤,直到DFA中所有状态都在任意一个输入符号下找到了目标状态,说明DFA的状态转换表Dtran构造完成。与此同时,DFA的集合也构造完成。
在构造过程中,需要使用以下重要的函数:
函数名 |
功能 |
closure(T) |
能够从T中的某个NFA状态s开始只通过ε转换到达的NFA的状态集合 |
move_Tc(T,c) |
能够从状态T中某个状态s出发通过输入符号c的转换到达的NFA状态的集合 |
伪代码:
子集构造算法
void subset(){
标签初始化 ,标签作用:标记还没有构造出边的状态
初始状态设置为NFA的初始状态0的闭包T
将初始状态T加入Dstate,作为DFA的第一个状态
while(存在没有被标记的状态T){
给T加标记,说明T要作为出发状态去查找输入符号的跳转状态
对于状态集合T,在输入符号为charSet[i]下,跳转到的状态集合U
for(对于任意一个输入符号a){
U = closure_T(moveTc(T,a));
if(U不在Dstate状态集合中){
if(U包含NFA中的接受状态){
将U设置为接受状态
}
将U加入DFA的状态集合
}
对当前状态T和输入符号a构造状态转换到达状态U
}
}
构造完毕,将DFA状态数目设置为当前状态数目
}closure(T)算法
__int64 closure_T(__int64 T){
将T中所有状态压入stateStack栈中
将closure(T)初始化为T,即需要包含自身状态
while(stateStack栈不为空){
将栈顶状态t弹出
for(每个满足如下条件的u:从t出发有一个标号为空的转换到达u){
if(u不在closure(T)中){
将u加入closure(T)中;
将u压入stataStack栈中;
}
}
返回新的状态集合
}Ø 等价划分算法:
算法思想:将一个DFA的状态集合划分成多个组,每个组中的各个状态之间互相不可区分。然后将每个组中的状态合并成minDFA的一个状态。算法在执行过程中维护了状态集合的一个划分,划分中每个组内各个状态尚不能区分,但是来自任意两个集合的不同状态是可以区分的。当任意一个组都不能被分解为更小的组的时候,这个划分就不能再一步精化,这样就可以得到minDFA。
算法步骤:
①将DFA的所有状态划分为两个集合:不包含接受状态的集合T1,包含接受状态的集合T2;以这两个为基础,进行集合划分。
②对于现有状态集合中任意一个状态集合T,对于一个输入符号a。新建状态集合数组U,数组对应长度为当前DFA状态个数。设立flag标识,为0表示不需要再划分。
③记录T中第一个状态经过a到达的状态x。依次检查T中第二个、第三个状态.....;如果第i个状态经过a到的状态不为x而为y,那么表示当前划分集合仍需要划分,将flag设置为1,同时将第i个状态从状态集合T中删除。同时将状态i加入一个y对应的U数组中的集合。如果第j个状态进过a到达的状态也为y,就将状态j也加入到y对应的U数组中的集合。
④将新产生的划分U加入到原来的划分T中;
⑤回到第二步执行,直到flag为0,说明不需要再进行划分,minDFA状态集合构造完毕。
void minDFA(){
初始化分为接受状态组和非接受状态组
对于当前每一组进行划分
while(flag为1,仍有组需要划分){
flag = 0;
数组goalSet(与当前minDFA分组数目相同)记录组别对应产生的新组
for(对于当前分组中的所有状态){
for(对于每一个输入符号){
if(i为组内第一个状态){
记录i经过符号j到达状态组T
}
else if(如果i经过符号j到达的状态组为Q){
flag=1;
将i从状态组T中删除
将i加入到Q对应的goalSet中
}
}
}
将goalSet中不为空的组并入旧组
当前minDFA状态数目等于原本状态数目+新状态数目
}
划分结束,构造状态转换表
} Ø 验证算法:
算法思想:验证两种自动机描述的语言是十分困难的。所以采用打印一定的长度范围内的语言集列表并进行对比。如果输出的语言集是相同的,那么说明NFA到DFA、DFA最小化是正确的,反之则是错误的。
语言集列表显示:采用深度优先算法,使用递归方法,以深度dep作为需要输出的字符串的下标。每次递归依次尝试字符集中所有字符,如果当前状态在当前输入符号下到达的状态不为-1,那么说明没有错误,将当前符号添加到字符串集合中,可以进行第dep+1层的递归。如果当前状态为接受状态,那么说明目前字符串[0:dep]符合DFA规则,打印字符即可。结束条件为递归深度大于N时,说明递归完成,直接返回。
伪代码:
void findSentence(int curIndex,int dep,int N,char *sen){
if(dep>N)return;//遍历结束
检查当前状态是否为接受状态,如果是,则输出sen[0:dep]
for(遍历字符集合){
int nxtIndex = 当前状态下当前输入符号下可以到达的状态;
if(下一状态不为-1){
将当前字符串中第dep个字符设为当前输入符号
findSentence(nxtIndex,dep+1,N,sen);//进行深度遍历
}
}
}1. 类的定义
概述:将实验中需要的NFA、DFA以及minDFA所有需要的数据成员和函数都定义在NFAtoDFA类中。方便调用、检查。
类成员一览表:
类型 |
名称 |
描述 |
私有数据成员 |
int charNum |
符号个数 |
char *charSet |
符号表 |
|
int NstateNum |
NFA状态个数 |
|
int NaccState |
NFA接收状态 |
|
vector |
NFA状态转换表 |
|
int DstateNum |
DFA状态编号 |
|
__int64 *Dstate |
DFA状态由NFA状态构成 2^i 第i位为1表示该状态包含NFA中的第i个状态 |
|
int DaccStateNum |
DFA接收状态个数 |
|
int *DaccStateSet |
DFA接收状态集 |
|
int minDstateNum |
最小DFA状态编号 |
|
__int64 * minDstate |
最小DFA状态集合,由DFA状态构成 2^i , 第i位为1表示该状态包含NFA中的第i个状态 |
|
int minDaccStateNum |
最小DFA接收状态个数 |
|
int *minDaccStateSet |
最小DFA接收状态集合 |
|
int **minDtran |
最小DFA状态转换表 |
|
私有函数成员 |
int charIndex(int charn) |
查找字符charn 在字符集合中的下标 ,如果没有找到返回-1 |
__int64 closure_T(__int64 T) |
求状态T的闭包 |
|
__int64 moveTc(__int64 T,char c) |
求状态T经过输入状态c到达的状态集合 |
|
__int64 haveUntagState(bool tag[],int curDstateNum) |
服务于subset函数 ,查看当前DFA状态集合中是否还有未被标记为已构造的状态转换表的函数。如果有, 返回第一个状态该状态;如果没有,返回-1 |
|
int DstateIndex(__int64 T,int curDstateNum) |
服务于subset函数,返回状态T的下标 |
|
bool includeAcc(__int64 U) |
服务于subset函数,查看 U中是否包含NFA中的接受状态,如果有返回true,如果没有返回false |
|
void initDFA() |
对DFA初始化,包含状态集合的内存分配等等 |
|
bool isDacc(int s) |
回s状态是否属于DFA状态中的接受状态 |
|
bool isMinDacc(int s) |
返回状态s是否为minDFA的接受状态 |
|
void subset() |
子集构造法,NFA->DFA |
|
void initMinDFA() |
初始化minDFA,包括状态集合的内存分配等等 |
|
void minDFA() |
等价划分算法,DFA->minDFA |
|
void NLanguage(int cur,int dep,int N,char*set) |
输出NFA语言集的递归函数 |
|
void DLanguage(int cur,int dep,int N,char*set) |
输出DFA语言集的递归函数 |
|
void minDLanguage(int cur,int dep,int N,char*set) |
输出minDFA语言集的递归函数 |
|
公有函数成员 |
bool NFA_init() |
NFA初始化,即读取NFA文件,构造状态转换表 |
void print_Ntran() |
打印NFA状态转换表 |
|
void test_closure(__int64 x) |
测试闭包函数 |
|
void test_moveTc() |
测试move[T,c] |
|
void print_Dtran() |
打印 DFA状态转换表 |
|
void print_minDtran() |
打印minDFA状态转换表 |
|
void NFALan(int N) |
输出字符长度为N的NFA语言集 |
|
void DFALan(int N) |
输出字符长度为N的DFA语言集 |
|
void minDFALan(int N) |
输出字符长度为N的minDFA语言集 |
2. 程序模块间的层次关系
Ø 概述:主要的算法被封装为类的私有成员,输出状态转换表和语言集等函数被当做外部接口,以便检查。下面将主要描述外部接口调用内部函数的关系图。
Ø 构造自动机模块:NFA->DFA和DFA->minDFA的过程在构造NFA完成后就被实现。换而言之,只要调用了NFA_init函数后,开始使用subset()函数构造DFA;DFA构造结束后,使用minNFA()函数构造minDFA。不需要用户手动去执行构造DFA和minDFA的函数。
Ø 子集构造法sunset()函数生成DFA:进入函数后首先调用了init_DFA()初始化了DFA的相关数据;其次在构造DFA的状态集时调用了closure(T)函数、move_Tc()函数以及其他比较基础的工具函数。
Ø 等价划分法minDFA()函数:进入函数后首先调用了initMinDFA()函数初始化了minDFA的相关数据;之后基本没有再调用其他函数。但是主要可以分为两块:第一部分是将DFA中的状态进行分组构成minDFA的状态集合;第二部分是根据DFA状态转换表构造minDFA的状态转换表。
Ø 语言集列表显示:三种状态机调用语言集的模块层次相同,所以以NFA距离来说。严格来说,这不是一个树。因为此算法采用递归方法求解,所以Nlanguage()结点有一个自旋边,该函数中参数较多且其中涉及私有数据成员的使用,故而不能作为外部接口,因此增加NFALan()函数作为公有函数调用Nlanguage()函数。
1. 文件清单
文件名 |
用途 |
success.cpp |
实验源码 |
example1.txt |
测试样例1:(a|b)*abb;来自教材实例 |
example2.txt |
测试样例2:(aa|b)*(a|bb)* 来自实验要求 |
example3.txt |
测试样例3:(a*|b*)*;来自教材练习 |
实验报告 |
本文档 |
五、实验测试:
样例一:(a|b)*abb
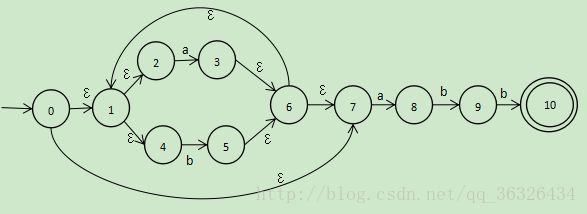
NFA状态转换图:
NFA状态转换表:
状态 |
a |
b |
ε |
0 |
-1 |
-1 |
1,7 |
1 |
-1 |
-1 |
2,4 |
2 |
3 |
-1 |
-1 |
3 |
-1 |
-1 |
6 |
4 |
-1 |
5 |
-1 |
5 |
-1 |
-1 |
6 |
6 |
-1 |
-1 |
1,7 |
7 |
8 |
-1 |
-1 |
8 |
-1 |
9 |
-1 |
9 |
-1 |
10 |
-1 |
10 |
-1 |
-1 |
-1 |
程序构造DFA状态转换表并根据其构造状态转换图:
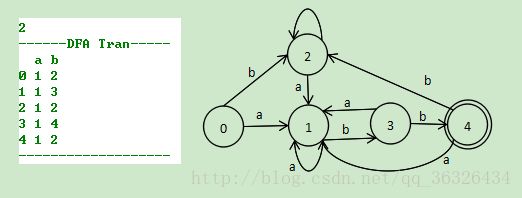
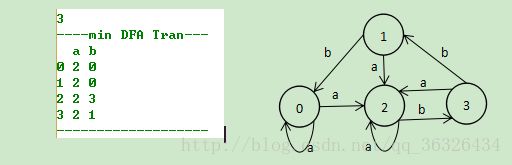
程序构造minDFA状态转换表并根据其构造状态转换图:
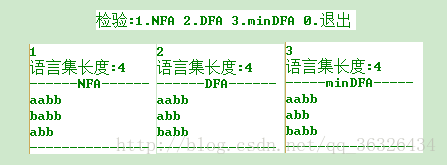
打印语言集对比三个状态机描述语言相同:
样例二:(aa|b)*(a|bb)*
打印状态转换表:
对比语言集:(由于空串的存在,NFA会产生重复的语言集)
样例三:(a*|b*)*
打印状态转换表
打印语言集(由于空串的存在,NFA会产生重复的语言集)
一、实验心得:
此次实验通过用代码实现NFA转化为DFA和DFA最小化,让我去思考如何实现教材上提供到的子集构造算法和最小化DFA算法,了解其实现的过程。
依据伪代码去实现让我考虑到了更多算法的细节。例如:
①在子集构造法构造DFA时,教材上只是讲了要给状态加标记,读了书之后没有怎么理解。在用代码实现时才发现是为了能够确定哪些状态还没有对其构造状态转换边。最终使得DFA状态转换表满秩。
②子集构造法是在构造DFA状态的同时,构造好其状态转换表。而等价划分法构造minDFA只负责将状态划分好状态,需要重新根据DFA状态转换表重新构造minDFA的状态转换表。
③书上介绍的等价划分算法是有一些迷惑性的。如果按照其伪代码来写,就有可能进入死循环。用书上的例子来说,A和B同时经过输入符号c到达了状态E。其达到了伪代码所述的划分条件,但却是不应该被划分的。按照伪代码所述,就会一直对AB进行划分,陷入死循环。经过了认真得查错后,我发现应该将其“两个状态经过同一输入符号时到达同一状态集合”的要求应该放在划分依据之中,而不是判断条件。所以我对其进行了改进,将状态集合中所有状态经过同一输入符号到达的状态集合不同作为划分依据,对集合进行划分,消除了死循环。
④理解了教材中所讲的死状态是什么意思。实验中将NFA转化为DFA过程中,DFA状态转换图出现了以下情况:状态6经过a和b都到达了自身,且状态6并不是接受状态。这表明到达状态6的串将永远不会被接受。进一步查看状态6是由哪些NFA状态构成的,发现没有状态6中没有任何一个NFA状态,即状态6为空集合。经过分析,发现这是因为DFA是要求任意一个状态对于所有的输入符号都有一条边到达其他状态。子集构造法为了满足这一点,在构造DFA时,将空集合也作为了一个DFA状态。
同时也学习到了一些编程的好方法,例如实验要求中推荐使用__int64型的T来存放状态集合。这种方法优点是非常高效,查找方便。缺点是可以存放的状态数有限。从优点角度分析,如果没有想到这种方法,我可能会去考虑使用一个数组或者链表来存储状态集合,那么占用的内存与查找时消耗的时间是非常可怕的。使用__int64类型的T来存放状态,如果我想查找一个状态i是否存在于状态集合T中,只需要判断((1<
在写完代码后,发现了此次代码中的一些不足。
①将三个状态机的所有数据和函数全部封装在了一个类中,仅仅是使用数据方便,却导致整个类十分庞大且复杂。使用起来层次关系也不够分明,代码并不优雅。
②函数封装不足且部分函数功能不够明确。例如minDFA()函数,使用了四层循环嵌套,其中部分循环本可以调用一个函数来实现。但是因为前期考虑没有到位,写完之后才发现。下次可以在编写代码之前大致考虑一下什么功能会被重复使用,将其写成一个函数,这样使代码清晰易懂。
③命名的不足,因为需要使用的数据太多。很多变量和函数名不清晰,导致在编写过程中出现了很多变量名使用错误的情况。这样编写代码的效率十分低下。变量和函数名应该与其含义和功能相关联,在使用时可以很明确的了解到其返回值可能是什么。例如haveUntagState()函数,其功能是返回没有被标记的状态。但是看这个函数名,反而像是返回了其有没有未被标记的状态。在函数使用了过程中就出现了应用的错误。如果使用untagState()可能一言就可以看出其返回值,使得代码更可读。
实验结束了,但是可以思考的地方还是很多的。在以后的实验中吸取教训,发扬优点~