回文串系列
目录
- 导言
- No.1 单一回文串
- No.2 最长回文子串
- 中心扩展法
- 动态规划法
- No.3 回文子串
- No.4 分割回文串 I
- No. 5 分割回文串 II
导言
回文,顾名思义就是正着读倒着读都是一样的,回文字符串系列问题在字符串问题中占了很大的比重,通过回文串可以延伸出很多相类似的题目,会用到不同的算法,各有千秋,例如动态规划、分治、回溯、双指针、递归等算法。下面就从最简单的回文字符串开始一步步深入讨论。
No.1 单一回文串
一个最简单的题目就是给出一个字符串,判断是否是回文串,其中这个字符串只包含连续的字母,忽略大小写,如:‘aca’,'abcd’这样。
算法思路
最简单也最常用的方法是双指针法,通过首尾判断两两是否相等,直到字符串中间位置。时间复杂度O(N),就遍历了一次字符串,空间复杂度O(1),没有额外开辟空间。
代码
Class Solution{
public boolean isPalindrome(String s){
if(s == null || s.length() == 0) return true;
int left = 0,right = s,length()-1; //left,right分别从字符串两边开始遍历
while(left < right){
if(s.charAt(left) == s.charAt(right)){
left++;
right--;
}
else return false;
}
return true;
}
}
简单变化一下,在字符串中加入空格,大小写字母,标点或者其他非字符符号,例如:“A man, a plan, a canal: Panama” ,这样的字符串,判断其字母部分是否是回文串。
本题是LeetCode 125 号题目
算法同样是双指针算法,但是要把非字母字符、空格、大小写给处理掉,步骤如下:
- 设置左、右双指针,向中间判断;
- 跳过非字符字母的字符;
- 将字母全部转化为小写体,之后判断;
其中可以使用Java中的库函数,也可以自己实现库函数的功能。
代码
class Solution {
public boolean isPalindrome(String s) {
if(s == null || s.length() == 0) return true; //边界处理
int l = 0,r = s.length()-1;
String str = s.toLowerCase(); //提前将整个字符串转换为小写
while(l<r){
if(!Character.isLetterOrDigit(str.charAt(l))) {
l++;continue; //跳过非字母字符,结束当前循环,并继续判断下一个字符
}
if(!Character.isLetterOrDigit(str.charAt(r))) {
r--;continue; //跳过非字母字符,结束当前循环,并继续判断下一个字符
}
if(str.charAt(l)!= str.charAt(r)) return false; //非回文串返回false
l++;r--;
}
return true;
}
}
复杂度分析:时间复杂度O(N),空间复杂度O(N),我们将原字符串转换为小写之后存放在一个新字符串中。
总结上述两个题目,算法都是一样的,只不过后者处理了一些非字母字符的情况,下面继续变通,在此基础上,判断一个字符串中的最长回文串,以及回文串的全排列(回文子串)等等。
No.2 最长回文子串
本题是LeetCode 5 号题目
题目
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
本体看似简单,但是要做出来确实需要扎实的算法基础,解题方法不少于4中,暴力解法、中心扩展、动态规划、Manacher’s Algorithm 马拉车算法,暴力解法不推荐,马拉车算法可以参考大佬的题解
下面主要看看中心扩展和动态规划两种方法,这两种方法在字符串问题中经常用到。
中心扩展法
中心扩展,顾名思义就是从中间向两边扩展,判断两边是否是相等,相等就左减右加。
遍历方式有三种:
- 以位置i为中心,先向左遍历,相等就将左边位置减一,直到左边的字符和当前位置的字符不等或到最左边位置结束;
- 同样以位置i为中心,向右遍历,相等就将右边位置加一,直到右边的字符和当前位置的字符不等或到最右边位置结束;
- 还是以位置i为中心,左右同时遍历,直到不等结束。
我们用 ‘abcdbbdaa’ 举例,当遍历到位置3时,过程如下:
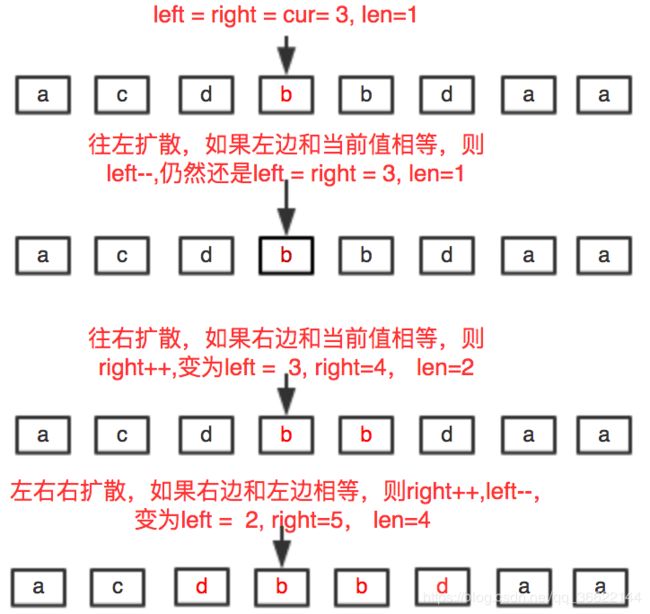
在编码是需要用maxlen用于记录最长回文串的长度,len记录以位置i为中心的最长回文串长度,同时还需要记录最长回文串的开始位置start。代码如下:
class Solution {
/*************中心扩展发法********************/
public String longestPalindrome(String s) {
if(s == null || s.length() == 0) return "";
int maxlen = 0,start = 0; //maxlen用于记录回文串长度,start用于记录开始位置
for(int i = 0;i < s.length();i++){
int l = i-1,r = i+1,len = 1;
while(l >= 0 && s.charAt(l) == s.charAt(i)) { //aab的请况,这里判断是位置 l 和 i比较,而不是l和r比较,因为是和i左边的比较
l--;
len++;
}
while(r < s.length() && s.charAt(i) == s.charAt(r)){//当i=1会重复计算aab的情况
r++;
len++;
}
while(l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)){ //aba这种情况,当为中间位置
l--;
r++;
len = len + 2;
}
if(maxlen < len){
maxlen = len;
start = l + 1;//由于前面进行 l--的操作,会将l的值减1,则开始位置需要加1
}
}
return s.substring(start,start+maxlen);
}
}
复杂度
时间复杂度:O(N^2),for循环下有一个while循环,双层循环
空间复杂度:O(1),没有额外开辟空间
看似时间和空间复杂度都不高,但是这种方法会重复计算很多不必要的值,例如aab形式,当中心位置为第一个a和第二个a时,会重复计算aa这个值。
动态规划法
动态规划的基础知识可以参考我的文章 动态规划(Dynamic Programming)里面介绍了 什么是动态规划以及动态规划的特点和一些例子,有助于理解本题。
对于这道题目而言,怎么将动态规划用于其中呢,说实话,当时做这道题目时真的没想到,而这也是动态规划的巧妙之处,动态规划能够解决上面中心扩展法重复计算的值,从而提高效率。话不多说,下面是整个算法思路。
"动态规划"最关键的步骤是想弄清楚状态如何转换,实际上,"回文"原本就具有"状态转移"的性质:
一个回文串去掉头尾以后,剩余部分仍然是回文的
依然从回文串讨论:
1、如果一个字符串的两端的两个字符不等,那么这个字符串就一定不是回文串;
2、如果一个字符串头尾两端字符串相等,才有继续往下
走的必要;
1)如果里面的字符串是回文串,整体就是回文串;
2)如果里面的字符串不是回文串,整体就不是回文串。
所以,在头尾字符相等的情况下,里面的字符串的回文性质决定了整个字符串的回文性子,因此,可以把“状态”定义为原字符串的一个子串是否为回文串。
第一步 定义状态
dp[i][j] 表示字符串s[i,j]是否为回文串,为布尔类型。
第二步 思考状态转移方程
通过上面讨论(头尾字符串是否相等),可以得到:
dp[i][j] = (s[i] = s[j]) and dp[i+1][j-1]
分析一下这个状态转移方程:
1)为什么是dp[i+1][j-1],举个例子,当字符串位置2和位置5的字符相等,即i=2,j=5,那么判断s[2,5]是否为回文串的关键就在于,位置3和位置4是不是回文串,即s[i+1,j-1]是不是回文串,这样就好理解多了。
2)“动态规划”实质就是填一张二维表格,i 和 j的关系必定是 i <= j,所以我们只需填充表格的上半部分;
3)在dp[i+1][j-1]中,需要考虑边界条件,即当[i+1,j-1]不构成区间时,即当长度小于2时,所以有
j-1 - (i+1) + 1 < 2 整理的 j-i < 3,加一的原因是闭合区间,少算了一个;j-i < 3这其实也比较好理解,当子串[i,j]的长度是2或3时,我们只需要判断头尾两个字符是否相等即可;
- 如果子串[i+1,j-1]只有一个字符,即在[i,j]的基础上去掉了两头,中间就一个字符,单个字符当然是回文的;
- 如果子串[i+1,j-1]为空,'aa’这种情况,i +1 ,j -1没有必要了,s[i,j]必然是回文的。
综上所述,在s[i] != s[j] 时,直接false,继续判断下一个区间;当s[i] == s[j] 时,j-i < 3的情况下,直接得出结论,dp[i][j] = true,否则才执行状态转移。
第三步 思考初始值
初始化时,单一字符肯定是回文的,即dp[i][i] = true;
事实上,初始化的部分都可以省去。因为只有一个字符的时候一定是回文,dp[i][i] 根本不会被其它状态值所参考。
第 4 步:考虑输出
在dp[i][j] == true的条件下,即s[i,j]为回文串,记录子串的开始位置和最大长度即可,最后通过开始位置和最大长度返回结果子串。
代码
/*************动态规划法********************/
public String longestPalindrome(String s) {
if(s == null || s.length() == 0) return "";
if(s.length() == 1) return s;
int len = s.length();
boolean[][] dp = new boolean[len][len];
for(int i = 0;i < len;i++) dp[i][i] = true;
int maxlen = 1,start = 0;//maxlen 的长度默认为1,至少是单个字符,所以不能默认为0
for(int j = 1;j < len;j++){
for(int i = 0;i < j;i++){//这里可以将i理解为左指针(left),j理解为右指针(right)
if(s.charAt(i) == s.charAt(j)){
if(j-i<3)
dp[i][j] = true;
else
dp[i][j] = dp[i+1][j-1];
}
else
dp[i][j] = false;
if(dp[i][j]){
if(maxlen < (j - i + 1)){ //更新maxlen的值并记录回文串的开始位置
maxlen = j - i + 1;
start = i;
}
}
}
}
return s.substring(start,start + maxlen);
}
复杂度分析
时间复杂度:O(N^2),双层for循环;
空间复杂度:O(N^2),引入了二维数组dp。
动态规划总结并优化
这里来讨论一下,为什么双层for循环 j在外层且初始值为1,那是因为我们在判断[i,j]是不是回文串时要去判断[i+1,j-1],即必须要先知道当前表格左下的值,我们的填表顺序就是下图第三幅图的填表顺序,其他几种也行,只不过相对更难理解。下面是一个大佬总结的几幅图和动态规划的相关理解和结论,可谓是相当精辟,后面有标注来源出处。
在给状态值赋值时,可以将代码优化一下,减少代码量,但复杂度不会变,且可读性更难。
下面一段代码
if(s.charAt(i) == s.charAt(j)){
if(j-i<3)
dp[i][j] = true;
else
dp[i][j] = dp[i+1][j-1];
}
else
dp[i][j] = false;
可以改为
dp[i][j] = s.charAt(i) == s.charAt(j) && (j-i<3 || dp[i+1][j-1])
下面是一个大佬总结的几幅图和动态规划的相关理解和结论,可谓是相当精辟,后面有标注来源出处。

图片参考
https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zhong-xin-kuo-san-dong-tai-gui-hua-by-liweiwei1419/
No.3 回文子串
本题是LeetCode 647 号题目
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被计为是不同的子串。
示例 1:
输入: “abc”
输出: 3
解释: 三个回文子串: “a”, “b”, “c”.
示例 2:
输入: “aaa”
输出: 6
说明: 6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”.
算法思路
本题实质就是求回文串的全排列,算法和上题完全类似,通过动态规划或中心扩展都可以求解,思路也一样,下面就动态规划解法介绍一下。
动态规划的状态定义,动态转移方程,初始化完全一样,只是输出值有所改变,无论输出值如何改变,都是和数组的值相关的,思考一下,我们要得到所有的回文串,数组中是回文串的值为true,所以true的个数即为最终的结果。复杂度也和上题一样。
代码
class Solution {
public int countSubstrings(String s) {
if(s == null || s.length() == 0) return 0;
int len = s.length(),res = 0;
boolean[][] dp = new boolean[len][len];
for(int i = 0;i < len;i++){
dp[i][i] = true;
res++;
}
for(int i = len-1;i >= 0;i--){
for(int j = i+1;j < len;j++){
dp[i][j] = s.charAt(i) == s.charAt(j) && (j-i < 3 || dp[i+1][j-1]);
if(dp[i][j]) res++;
}
}
return res;
}
}
No.4 分割回文串 I
本题是 LeetCode 131 号题
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: “aab”
输出:
[
[“aa”,“b”],
[“a”,“a”,“b”]
]
算法思路
本题刚拿到题目可能不知所措,但细细想想,首先回文串我们前面已经做过,这道题目也肯定是会用到的,其次就是如何将这些回文子串组合起来,相当求回文子串的全排列。所以思路就出来了,我们先将字符串中的回文子串找出来,然后再进行排列。
找回文串的方法同样用动态规划,而排列就可以用回溯法,通过递归的方式遍历回文串,剪枝。aabacz为例,如下图:
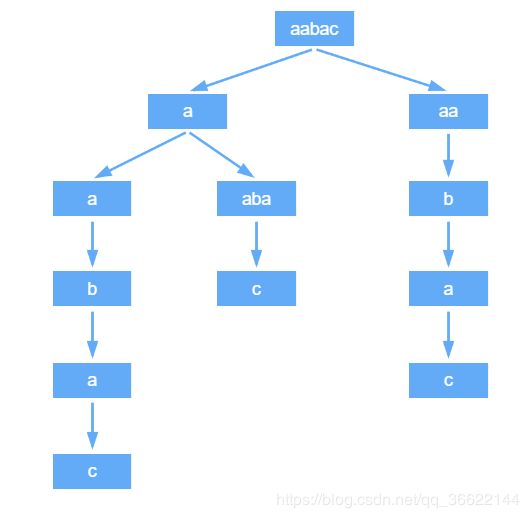
代码
class Solution {
List<List<String>> res = new ArrayList<>();
public List<List<String>> partition(String s) {
int len = s.length();
//动态规划处理数组,将回文子串标记出来
boolean[][] dp = new boolean[len][len];
for(int i = 0;i < len;i++) dp[i][i] = true;
for(int j = 1;j < len;j++){
for(int i = j;i >= 0;i--){
dp[i][j] = s.charAt(i) == s.charAt(j) && (j-i<3 || dp[i+1][j-1]);
}
}
dfs(dp, 0, len, s, new ArrayList<String>());
return res;
}
private void dfs( boolean[][] dp, int i, int n, String s, ArrayList<String> tmp) {
if (i == n) res.add(new ArrayList<>(tmp));
for (int j = i; j < n; j++) {
if (dp[i][j]) {
tmp.add(s.substring(i, j + 1)); //将s[i,j]子串加入tmp集合中
dfs(dp, j + 1, n, s, tmp);//从j+1开始递归
tmp.remove(tmp.size() - 1);//回删,继续循环下一个j,回溯的精髓
}
}
}
}
下面这个也是回文串的变形进阶,来看看吧!
No. 5 分割回文串 II
本题是 LeetCode 132 号题目
题目
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。返回符合要求的最少分割次数。
示例:
输入: “aab” 输出: 1 解释: 进行一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回文子串。
算法思路
首先我们会联想到上面一题,在上面一题的基础上计算结果,个开始我也是这种思路,这就很容易先入为主,虽然和上面一题有联系,也能够通过上一题的思路解答,但是这样不一定是最优的解决方案。
回归本题,要求最少的分割次数,字符串问题我们很容易想到动态规划,那我们不妨就用动态规划来思考一下。
一个字符串能够被分割成最少的回文串个数,求分割次数,那么少一个字符时的最少回文分割次数和当前有没有关系呢?答案是肯定的。下面通过动态规划的几大步骤一步步分析。
思考状态
我们定义dp[i]为字符串前i个的最少分割数。
思考状态转移方程
我们要求dp[i]的值,首先我们需要看0~i这部分有几个分割数,以j为边界,j比i小,如果s[j+1,j]是回文串,说明在j之前的基础上又多了一个分割,那么dp[i]的值就是dp[j]+1,要求最小的分割数,所以还需要通过min函数比较一下,所以有状态转移方程:
dp[i] = min([dp[j] + 1 for j in range(i) if s[j + 1, i] 是回文])
思考初始值
需要先初始化dp的初始值,将dp[i]赋值为i。
输出值
dp[length - 1] 即为我们要求的结果,即最后一个状态值。
综上,此题有两处需要用到动态规划的思想,一是求子串是否是回文串,二是求解最少的分割次数。
代码
class Solution {
public int minCut(String s) {
int len = s.length();
if(len < 2) return 0;
boolean[][] isPalindrome = new boolean[len][len];
int[] dp = new int[len];
for(int i = 0;i < len;i++){
dp[i] = i; //初始化状态值为i
}
//通过动态规划判断子串是不是回文
for(int j = 0;j < len;j++){
for(int i = 0;i <= j;i++){
isPalindrome[i][j] = s.charAt(i) == s.charAt(j) && (j-i < 3 || isPalindrome[i+1][j-1]);
}
}
//此处从第二个字符开始判断
for(int i = 1;i < len;i++){
if(isPalindrome[0][i]){ //s[0,i]为回文,则前i个数不用分割,dp[i]=0
dp[i] = 0;
continue;
}
for(int j = 0;j < i;j++){
if(isPalindrome[j+1][i]){//由于前面判断了s[0,i],所以此处从j+1处开始判断是否是回文
dp[i] = Math.min(dp[i],dp[j] + 1);
}
}
}
return dp[len-1];
}
}
通过两个题目的分析,一个回文子串可以延伸出一系列的题目,各种算法结合,使问题变复杂,所以解题是需要思考各个题目之间的联系,万变不离其宗,抓住核心算法进行思考,问题分解,然后思路就慢慢出来了。