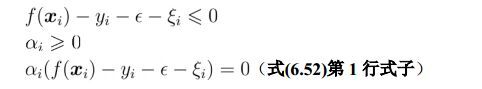西瓜书课后题——第六章（支持向量机）

课后题6.2、西瓜数据集3.0a上分别用线性核和高斯核训练一个SVM，并比较支持向量的区别。

使用LIBSVM经过训练之后发现，线性核和高斯核所得到的支持向量是一样的。LIBSVM的使用见这篇文章：LIBSVM使用

完整代码如下所示：

from libsvm.python.svmutil import *
import numpy as np
A = np.array([[0.697,0.460,1],[0.774,0.376,1],[0.634,0.264,1],[0.608,0.318,1],[0.556,0.215,1],
     [0.403,0.237,1],[0.481,0.149,1],[0.437,0.211,1],[0.666,0.091,-1],[0.243,0.267,-1],
     [0.245,0.057,-1],[0.343,0.099,-1],[0.639,0.161,-1],[0.657,0.198,-1],[0.360,0.370,-1],
     [0.593,0.042,-1],[0.719,0.103,-1]])
y = A[:,2]
x = []
for i in range(len(y)):
    dic = {}
    dic[1] = A[i,0]
    dic[2] = A[i,1]
    x.append(dic)

lina_options = '-t 0 -c 1 -b 1'      #线性核
guass_options = '-t 2 -c 4 -b 1'     # 高斯核
model = svm_train(y,x,lina_options)
svm_save_model('./xiGua3.3alpha_linear',model)
model_ = svm_train(y,x,guass_options)
svm_save_model('./xiGua3.3alpha_Guass',model_)

得到的支持向量如下所示： 

1     1:0.697     2:0.46 
1     1:0.774     2:0.376 
1     1:0.634     2:0.264 
1     1:0.608     2:0.318 
1     1:0.556     2:0.215 
1     1:0.403     2:0.237 
1     1:0.481     2:0.149 
1     1:0.437     2:0.211 
-1    1:0.666     2:0.091 
-1    1:0.243     2:0.267 
-1    1:0.343     2:0.099 
-1    1:0.639     2:0.161 
-1    1:0.657     2:0.198 
-1    1:0.36      2:0.37 
-1    1:0.593     2:0.042 
-1    1:0.719     2:0.103

 

课后题6.3、用UCI数据集，分别用高斯核和线性核进行训练。

此处，选用了 iris数据集 中的前两类，分别标记为1和-1。用前40个样本进行训练，用后10个样本进行测试。

具体代码如下：

import numpy as np
from libsvm.python.svmutil import *

def readData():    # 读取数据
    """
    Read data from txt file.
    Return:
        X1, y1, X2, y2, X3, y3: X is list with shape [50, 4],
                                y is list with shape [50,]
    """
    X1 = []
    y1 = []
    X2 = []
    y2 = []
    #read data from txt file
    with open("./iris.txt", "r") as f:
        for line in f:
            x = []
            iris = line.strip().split(",")
            for attr in iris[0:4]:
                aa = float(attr)
                x.append(aa)
            if iris[4]=="Iris-setosa":
                X1.append(x)
                y1.append(1)
            else:
                X2.append(x)
                y2.append(-1)
    return X1, y1, X2, y2

def getX(X):              # 生成LIBSVM需要的固定数据格式
    A = []
    X = np.array(X)
    m,n = np.shape(X)
    for i in range(m):
        dic = {}
        for j in range(n):
            dic[j+1] = X[i,j]
        A.append(dic)
    return A

def svm_linear(x,y):       # 线性核训练
    lina_options = '-t 0 -c 1 -b 1'      #线性核
    model = svm_train(y,x,lina_options)
    svm_save_model('./problem_6.3/UCI_linear',model)

def svm_guass(x,y):      # 高斯核训练
    guass_options = '-t 2 -c 4 -b 1'     # 高斯核
    model = svm_train(y,x,guass_options)
    svm_save_model('./problem_6.3/UCI_guass',model)

def predic_linear(x,y):     # 线性核预测
    model = svm_load_model('./problem_6.3/UCI_linear')
    p_label,p_acc,p_val = svm_predict(y,x,model)
    return p_label,p_acc

def predic_guass(x,y):      # 高斯核预测
    model = svm_load_model('./problem_6.3/UCI_guass')
    p_label,p_acc,p_val = svm_predict(y,x,model)
    return p_label,p_acc

def main():
    X1,y1,X2,y2 = readData()

    x1 = getX(X1)
    x2 = getX(X2)

    x_train = x1[:40]
    y_train = y1[:40]
    x_train.extend(x2[:40])
    y_train.extend(y2[:40])

    x_test = x1[40:]
    x_test.extend(x2[40:])
    y_test = y1[40:]
    y_test.extend(y2[40:])

    svm_linear(x_train,y_train)
    svm_guass(x_train,y_train)
    p_label_lin,p_acc_lin = predic_linear(x_test,y_test)
    p_label_gua,p_acc_gua = predic_guass(x_test,y_test)
    print("线性预测结果")
    print(p_label_lin,p_acc_lin)
    print("高斯预测结果")
    print(p_label_gua,p_acc_gua)


if __name__ == '__main__':
    main()

最终可以发现，使用 线性核 得到的模型内容如下所示，仅有3个支持向量，第一类2个，第二类1个：

svm_type c_svc
kernel_type linear
nr_class 2
total_sv 3
rho -0.77382525930929269
label 1 -1
probA -2.4478146893743347
probB -0.35294488993985529
nr_sv 2 1
SV
0.21830366492064313     1:5.1     2:3.3     3:1.7     4:0.5 
0.34115593497309121     1:4.8     2:3.4     3:1.9     4:0.2 
-0.55945959989373428    1:4.9     2:2.4     3:3.3     4:1 

使用高斯核得到的模型如下所示，有 7个支持向量，第一类有4个，第二类3个：

svm_type c_svc
kernel_type rbf
gamma 0.25
nr_class 2
total_sv 7
rho 0.13436257455469611
label 1 -1
probA -3.3718241673496236
probB -0.0081498851867360216
nr_sv 4 3
SV
0.67790332585451707     1:4.4     2:2.9     3:1.4     4:0.2 
0.58083107807394418     1:5.7     2:4.4     3:1.5     4:0.4 
0.25603598180822196     1:5.1     2:3.3     3:1.7     4:0.5 
0.53119467380522756     1:4.8     2:3.4     3:1.9     4:0.2 
-0.53179196812475671    1:7       2:3.2     3:4.7     4:1.4 
-1.3463704603213571     1:4.9     2:2.4     3:3.3     4:1 
-0.16780263109579691    1:6.7     2:3       3:5       4:1.7 

但是，使用两个不同的核函数，在测试集上的精确度均为 100% 。预测的结果如下所示：

线性预测结果
[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0]            (100.0, 0.0, 1.0)
高斯预测结果
[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0]            (100.0, 0.0, 1.0)

 课后题6.4、讨论线性判别分析和线性核支持向量机在何种条件下等价。

此题的解释参见这篇文章：https://blog.csdn.net/icefire_tyh/article/details/52135662

个人结合参考文章中博主的解释及文章末尾的评论，整理如下：

分以下几点进行一个理解：

     1. LDA和线性SVM都希望能最大化异类样例间距，但LDA是异类中心间距最大化，而线性SVM考虑的是支持向量间距最大

     2. LDA的目标函数考虑了同类样例的协方差，希望同类样例在投影空间尽可能靠近，而线性SVM却没有考虑这一点。

     3.关于数据是否线性可分的问题，如果使用软间隔的线性SVM，线性可分这个条件是不必要的，如果是硬间隔线性SVM，那么线性可分是必要条件。但是LDA不管数据是否线性可分，都可以进行处理

     4. 假如当前样本线性可分，且SVM与LDA求出的结果相互垂直。则当SVM的支持向量固定时，再加入新的非支持向量样本，并不会改变SVM中求出的w。但是新加入的样本会改变原类型数据的协方差和均值，从而导致LDA求出的结果发生改变。这个时候两者的w就不再垂直，但是数据依然是可分的。所以， 线性可分  和   LDA求出的wl与线性核支持向量机求出的ws垂直，这两个条件是不等价的。

     5. 所以，该题的答案严格上来讲，应该是当线性SVM和LDA求出的w互相垂直时，两者是等价的。因为一般LDA是不带偏置项的（因为LDA的思想是投影，投影过程和偏置是没有任何关系的），所以SVM这个时候比LDA仅仅多了个偏移b。

 

课后题6.5、高斯核SVM和RBF之间的联系。

参考这篇博客： https://blog.csdn.net/icefire_tyh/article/details/52135662         

个人整理如下几点：

      1、RBF网络的径向基函数与SVM都采用高斯核，就分别得到了高斯核RBF网络与高斯核SVM。

      2、神经网络是最小化累计误差，将参数 w 作为惩罚项；而SVM相反，主要是最小化参数，将误差作为惩罚项。

      3、根据书上给出的公式，可以发现，在二分类问题中，如果将RBF中隐层神经元的个数设置为总样本个数，且每个隐层神经元所对应的中心设置为样本参数，并将RBF的径向基函数中的 beta 设置成高斯函数中对应的系数，则得出的RBF网络与核SVM基本等价，非支持向量在RBF中将得到很小的权重。

 

课后题6.6、SVM对噪声敏感的原因。

参考这篇博客：https://blog.csdn.net/Dby_freedom/article/details/82960422       

个人整理如下：

        1、SVM的基本形态是一个硬间隔分类器，它要求所有样本都满足硬间隔约束（即函数间隔要大于1）

        2、当数据集中存在噪声点但是仍然满足线性可分的条件时，SVM为了把噪声点也划分正确，超平面就会向另外一个类的样本靠拢，这就使得划分超平面的几何间距变小，从而降低了模型的泛化性能。

        3、当数据集因为存在噪声点而导致已经无法线性可分时，此时就使用了核技巧，通过将样本映射到高维特征空间使得样本线性可分，这样就会得到一个复杂模型，并由此导致过拟合（原样本空间得到的划分超平面会是弯弯曲曲的，它确实可以把所有样本都划分正确，但得到的模型只对训练集有效），泛化能力极差。

        4、所以说，SVM对于噪声很敏感。因此，提出了软间隔SVM来防止由于噪声的存在而导致的过拟合问题。

 

课后题6.7、给出式6.52的完整KKT条件。

首先，根据KKT条件的定义，可以知道，对于拉格朗日函数中的带有拉格朗日乘子的项，每一项对应的KKT条件共有三个式子。在式6.52中，带有拉格朗日乘子的共有四项，所以完整的KKT条件应该共有12个式子。

完整的KKT条件如下所示：

 

课后题6.8、以密度为输入，含糖率为输出，训练一个SVR。 

 采用 epsilon-SVR进行回归，核函数采用高斯核，具体代码如下：

from libsvm.python.svmutil import *
import numpy as np
A = np.array([[0.697,0.460],[0.774,0.376],[0.634,0.264],[0.608,0.318],[0.556,0.215],
     [0.403,0.237],[0.481,0.149],[0.437,0.211],[0.666,0.091],[0.243,0.267],
     [0.245,0.057],[0.343,0.099],[0.639,0.161],[0.657,0.198],[0.360,0.370],
     [0.593,0.042],[0.719,0.103]])
y = A[:,1]
x = []
for i in range(len(y)):
    dic = {}
    dic[1] = A[i,0]
    x.append(dic)

guass_options = '-s 3 -t 2 -c 1 -b 1'     # 高斯核
model = svm_train(y,x,guass_options)
svm_save_model('./problem_6.8_XG3.3alpha_guass',model)

最终训练得到的模型如下所示：

svm_type epsilon_svr
kernel_type rbf
gamma 1
nr_class 2
total_sv 9
rho -0.21442336320877067
probA 0.11761725324207717
SV
1                          1:0.697 
1                          1:0.774 
0.67138842799068921        1:0.608 
-1                         1:0.666 
0.32861157200931085        1:0.243 
-1                         1:0.245 
1                          1:0.36 
-1                         1:0.593 
-1                         1:0.719 

上面第一列其实是每一个支持向量的权值，对应于西瓜书上式6.47里面的（alpha‘ - alpha）

 不妨令模型中第一列为alpha，第二列为 x, 则根据书上公式6.47及式6.56，结合训练得到的模型和核函数是高斯核的情况，我们可以得到如下的含糖率和密度之间的关系 ：

含糖率（x） = ∑ alphai * exp(-|x-xi|^2) + 0.2144

（因为高斯核是exp(-gamma*|u-v|^2)，而根据模型可知gamma为1，所以得到上式回归关系）