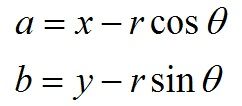encv —— HoughCircles 霍夫圆变换原理及圆检测
霍夫圆变换原理
霍夫圆变换的基本原理与霍夫线变换（https://www.cnblogs.com/bjxqmy/p/12331656.html）大体类似。
- 对直线来说，一条直线能由极径极角（r，θ）表示，而对于圆来说，我们需要三个参数：圆心（a，b），半径 r。
笛卡尔坐标系中圆的方程为：
化简便可得到：
- 对于（x0，y0），我们可以将通过这一点的所有圆统一定义为：
a = x0 - r·cosθ
b = y0 - r·sinθ
这就意味着每一组（a，b，r）代表一个通过点 
的圆。
-
对于一个给定点
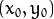，我们可以在三维直角坐标系中，绘出所有通过它的圆。最终我们将得到一条三维的曲线：
- 我们可以对图像中所有的点进行上述操作.。如果两个不同点进行上述操作后得到的曲线在空间 a - b - r 相交, 即它们有一组公共的（a，b，r），这就意味着它们在同一个圆上。
- 越多曲线交于一点，也就意味着这个交点表示的圆由更多的点组成。我们可以设置一个阈值，来决定多少条曲线交于一点我们才认为检测到了一个圆。
- 这就是霍夫圆变换要做的.。它追踪图像中每个点对应曲线间的交点.。如果交于一点的曲线的数量超过了阈值, 那么可以认为这个交点所代表的参数（a，b，r）在原图像中为一个圆。
以上是标准霍夫圆变换实现算法。问题是它的累加面（绘制三维曲线的空间）是一个三维的空间，意味着比霍夫线变换需要更多的计算消耗。OpenCV 霍夫圆变换对标准霍夫圆变换做了运算上的优化。它采用的是 “霍夫梯度法”。
霍夫梯度法的原理
- 估计圆心
- 把原图做一次 Canny 边缘检测，得到边缘检测的二值图。
- 对原始图像执行一次 Sobel 算子，计算出所有像素的邻域梯度值。
- 初始化圆心空间 N(a,b)，令所有的 N(a,b)=0。
- 遍历 Canny 边缘二值图中的所有非零像素点，沿着梯度方向 ( 切线的垂直方向 )画线，将线段经过的所有累加器中的点 (a,b) 的 N(a,b)+=1。
- 统计排序 N(a,b)，得到可能的圆心（N(a,b) 越大，越有可能是圆心）。
- 估计半径（针对某一个圆心 (a,b)）
- 计算 Canny 图中所有非 0 点距离圆心的距离。
- 距离从小到大排序，根据阈值，选取合适的可能半径（比如 3 和 3.5 都被划为半径值 3 中）。
- 初始化半径空间 r, N(r)=0。
- 遍历 Canny 图中的非 0 点，N( 距离 )+=1。
- 统计得到可能的半径值（N(r) 越大，说明这个距离值出现次数越多，越有可能是半径值）。
霍夫梯度法缺点
- 在霍夫梯度法中，我们使用 Sobel 导数来计算局部梯度，那么随之而来的假设是，其可以视作等同于一条局部切线，并这个不是一个数值稳定的做法。在大多数情况下，这样做会得到正确的结果，但或许会在输出中产生一些噪声。
- 在边缘图像中的整个非0像素集被看做每个中心的候选部分。因此，如果把累加器的阈值设置偏低，算法将要消耗比较长的时间。
- 因为每一个中心只选择一个圆，如果有同心圆，就只能选择其中的一个。
- 因为中心是按照其关联的累加器值的升序排列的，并且如果新的中心过于接近之前已经接受的中心的话，就不会被保留下来。且当有许多同心圆或者是近似的同心圆时，霍夫梯度法的倾向是保留最大的一个圆。可以说这是一种比较极端的做法，因为在这里默认Sobel导数会产生噪声，若是对于无穷分辨率的平滑图像而言的话，这才是必须的。
霍夫圆变换：HoughCircles 函数
HoughCircles 函数可以利用霍夫变换算法检测出灰度图中的圆。它相比之前的 HoughLines 和HoughLinesP，比较明显的一个区别是不需要源图像是二值的，而 HoughLines 和HoughLinesP 都需要源图像是二值图像。
void HoughCircles(InputArray image, OutputArray circles, int method, double dp, double minDist, double param1 = 100, double param2 = 100, int minRadius = 0, int maxRadius = 0);
- image，输入图像，即源图像，需要为 8 位的灰度单通道图像。
- circles，调用 HoughCircles 函数后此参数存储了检测到的圆的输出矢量，每个矢量由包含了 3 个元素的浮点矢量（x，y，radius）表示。
- method，使用的检测方法，目前 OpenCV 中就霍夫梯度法一种可以使用，标识符为 HOUGH_GRADIENT。
- dp，累加面分辨率（大小） = 原始图像分辨率（大小） × 1/dp。默认 dp = 1 时，两者分辨率相同。
- minDist，两个圆心之间的最小距离。若两圆心距离 < minDist，则认为是同一个圆。
- param1，Canny 边缘检测的高阈值，低阈值被自动置为高阈值的一半，默认为 100。
- param2，累加平面某点是否是圆心的判定阈值。它越大，能通过检测的圆就更接近完美的圆形，默认为 100。
- minRadius，圆半径的最小值。默认为 0。
- maxRadius，圆半径的最大值，默认为 0。
此函数可以很容易地检测出圆心，但是可能找不到合适地圆半径。我们可以通过 minRadius 和 maxRadius 两个参数指定最大和最小圆半径，来辅助圆检测的结果。或者可以直接忽略返回半径，让二者均为默认值，只用 HoughCircles 函数检测出圆心，用额外步骤进一步确定半径。
代码示例
#include
#include
using namespace std;
using namespace cv;
int hough_value = 55;
Mat src, gray;
void hough_change(int, void*) {
vectorcircles; //minDist 和 param2 数值的设定是关键
HoughCircles(gray, circles, HOUGH_GRADIENT, 1, 10, 110, hough_value, 0, 0);
Mat show = src.clone();
for (int i = 0; i < circles.size(); i++) {
circle(show, Point(circles[i][0], circles[i][1]), circles[i][2], Scalar(0, 0, 255), 2);
}
imshow("show", show);
}
int main() {
src = imread("C:/Users/齐明洋/Desktop/1.jpg");
GaussianBlur(src, src, Size(3, 3), 0, 0);
imshow("src", src);
cvtColor(src, gray, COLOR_BGR2GRAY);
namedWindow("show");
createTrackbar("hough_value", "show", &hough_value, 200, hough_change);
hough_change(0, 0);
waitKey(0);
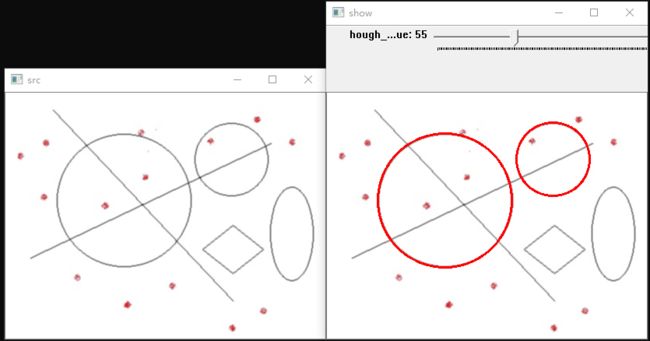
} 效果演示：
借鉴博客：https://www.cnblogs.com/yzl050819/p/7967526.html
https://www.cnblogs.com/lancer2015/p/6852488.html
https://blog.csdn.net/weixin_41049188/article/details/92422241?utm_source=distribute.pc_relevant.none-task